MIT线性代数公开课学习笔记第11~15课(矩阵空间、秩1矩阵和小世界图,图和网络,正交向量与子空间,子空间投影)

十一、矩阵空间、秩1矩阵和小世界图

1、矩阵空间

对于全体\(n\times n\)大小的实矩阵构成的集合\(\mathbb{R}^{n\times n}\)而言，其满足加法和数乘的封闭性，所以这个集合中的每个元素可以类比为向量，这个集合也是一个线性空间，称之为矩阵空间。

\(\mathbb{R}^{n\times n}\)最常见的几种子空间如下：

• (1)全体n阶实对称矩阵构成的集合\(S\)(symmetric matrix)，\(\mathrm{dim}S=\frac 1 2 n(n+1)\)

• (2)全体n阶实上三角矩阵构成的集合\(U\)(upper triangular matrix)，\(\mathrm{dim}U=\frac 1 2 n(n+1)\)

• (3)全体n阶实对角阵构成的集合\(D\)(diagonal matrix),\(\mathrm{dim}D=n\)

2、线性子空间的交、和

对于两个线性子空间\(W_1,W_2\)而言，它们的交与和定义为：

\[W_1\cap W_2=\{\alpha|\alpha\in W_1 \ \mathrm{ and } \ \alpha\in W_2\} \]

\[W_1+ W_2=\{\alpha+\beta|\alpha\in W_1 \ \mathrm{ and } \ \beta\in W_2\} \]

\[\mathrm{dim} W_1+\mathrm{dim} W_2-\mathrm{dim}(W_1 \cap W_2)=\mathrm{dim}(W_1+W_2) \]

对于之前1中提到的\(S\)和\(U\)而言，\(S\cap U=D\)，\(S+U=\mathbb R^{n\times n}\)

注意，"线性子空间的并(\(W_1 \cup W_2\))"不一定是线性空间，例如\(W_1\)代表一条过原点的直线上的全体向量，\(W_2\)代表一个过原点的平面上的全体向量，\(W_1 \cup W_2\)就是这条直线插在这个平面，那么\(W_1\)中任一非零向量和\(W_2\)中任一非零向量之和不属于\(W_1 \cup W_2\)，因此该集合不对加法封闭，不是线性空间。

3、微分方程

对于微分方程\(\frac{d^2y}{dx^2}+y=0\)而言，其通解是\(y=c_1sinx+c_2cosx\)，则这个方程的解空间的维度为2，解空间的一组基为\(\{sinx,cosx\}\)，这个方程的解空间显然对加法和数乘封闭，因此也是线性空间。

4、秩为1的矩阵的一些性质

对于\(n\times m\)的秩为1的矩阵\(A\)而言，它具有如下性质：

\(A=\alpha \beta^T\)(这里\(\alpha\)是n维列向量,\(\beta\)是m维列向量)

此外，任一秩为\(r\)的矩阵均可表示为\(r\)个秩为1的同型矩阵之和。

5、其他

定义集合

\[S=\{v|v\in \mathbb{R}^4,\sum_{i=1}^4v_i=0\} \]

显然该集合对加法和数乘封闭，是一个线性空间。

该集合可以视作是矩阵\(A=(1,1,1,1)\)的零空间。\(r(A)=1\)，所以\(N(A)=4-1=3\)。而\(\mathrm{dim}N(A^T)=0\),\(N(A^T)=\{0\}\)

十二、图和网络

1、图及其关联矩阵

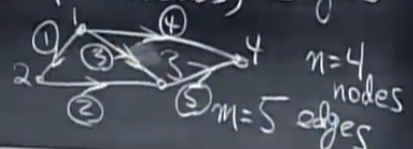
对于如上图所示的一个4个结点、5条边的有向图\(G\)(图中每条边旁圆圈内是其编号)而言，其关联矩阵\(A\)(incidence matrix)如下所示：

为方便叙述，以下默认\(A\)为\(n\times m\)大小矩阵

矩阵中第i行代表了图中的第i条边，如第一条边\((1\to 2)\)，则\(a_{1,1}=-1\)，\(a_{1,2}=1\)，-1表明该边从结点1离开，1表明该边到达结点2

图中第1、2、3号边构成了一条回路(注：准确地讲应该是平面图中的某一个区域)，对应于关联矩阵中第1、2、3行的行向量是线性相关的。

2、关联矩阵的零空间

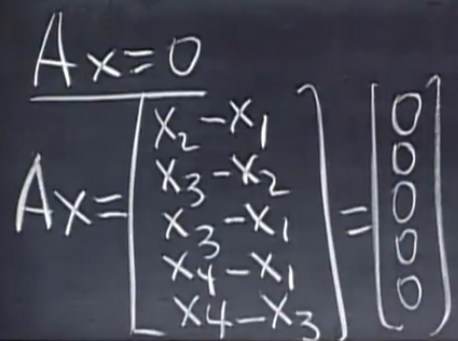
对于1中的关联矩阵\(A\)而言，其对应齐次线性方程组\(AX=0\)如上图所示

该方程组的物理意义是：寻找一组\(X=(x_1,x_2,\cdots,x_m)\)，即1到m号结点的电势分别为\(x_1,x_2,\cdots,x_m\)，使得图中每条边上无电流

显然\(N(A)=1\)，即\(AX=0\)的基础解系中只有一个解，该方程组通解可表示为\(k(1,1,\dots,1)^T\)，这表明在一个无外接电源的电路中，要保持各边上无电流，则所有结点电势相同

3、关联矩阵的左零空间

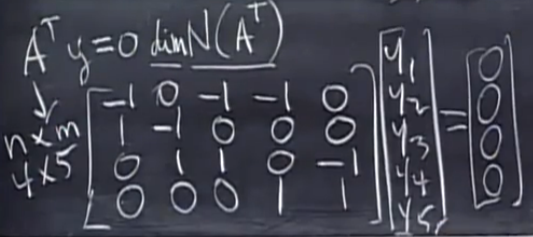
对于1中的关联矩阵\(A\)而言，齐次线性方程组\(A^TY=0\)如上图所示

该方程组的物理意义是：寻找一组\(Y=(y_1,y_2,\cdots,y_n)\)，边1到n上的电流分别为\(y_1,y_2,\cdots,y_n\)(这里的电流正方向为图G中每条边的方向)，使得整个电路满足基尔霍夫电流定律(KCL)

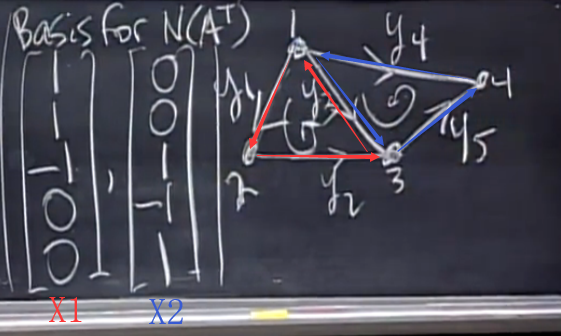
这里\(N(A^T)=2\)，\(A^T=Y\)的基础解系中包含两个解，分别代表了图G中只有某一个回路(注：准确地讲应该是平面图中的某一个区域)上有电流流过的情况。

那么所有\(Y\)的可行解都是这个基础解系的线性组合，即每个区域上电流分布的线性组合。

4、关联矩阵的行空间

\(A\)的行空间即\(A^T\)的列空间。

\(C(A^T)\)的基就是\(A\)的行向量的极大线性无关组，这组向量是线性无关的，表明它们对应的边不能构成一个回路，又因为这里\(G\)是联通图，因此一定能找到包含全部m个结点的生成树，\(C(A^T)\)对应的边构成了一棵树，即\(C(A^T)=m-1\)

5、总结

\(\mathrm{dim}N(A^T)=n-r(A)=|E|-r(A)\)(\(|E|\)是\(G\)的边的个数)

\(\mathrm{dim}N(A^T)=G\)中的区域个数

\(r(A)=C(A^T)=m-1=|V|-1\)(\(|V|\)是\(G\)的结点个数)

从而有

\[\mathrm{dim}N(A^T)=|E|-r(A)=|E|-|V|+1 \]

即\(G\)中区域个数=边的个数-顶点个数+1

令\(X\)为m个点的电势组成的列向量，\(A\)为无源(或只有电压源)电路对应的图\(G\)的关联矩阵，则\(e=AX\)为各边两边的点的电势差，\(Y=Ce\)为每条边上的电流(\(C\)为电导)，\(A^TY=0\)表明这个电流满足KCL定律

以上三个方程联立得到\(A^TCAX=0\)

如果考虑给该图加上电流源（图G中不包括该电流源及与之相连的边）的话，那么最后的\(A^TY=f\neq 0\)，\(A^TCAX=f\)，因为与电流源相连的结点都要考虑到电流源的电流的影响。

十四、正交向量与子空间

1、正交向量

对于两个列向量\(\alpha,\beta,\alpha^T\beta=0\)则这两个向量是正交的。

零向量与任何非零向量正交

\(\alpha,\beta\)正交，等价于\(\|\alpha\|^2+\|\beta\|^2=\|\alpha+\beta\|^2\)

• 证明：\(\|\alpha\|^2+\|\beta\|^2=\alpha^T\alpha+\beta^T\beta\)

• \(\|\alpha+\beta\|^2=(\alpha+\beta)^T(\alpha+\beta)=\alpha^T\alpha+\beta^T\alpha+\alpha^T\beta+\beta^T\beta\)

• \(\beta^T\alpha=\alpha^T\beta=0\)(两向量正交)，故\(\|\alpha\|^2+\|\beta\|^2=\|\alpha+\beta\|^2\)

2、正交子空间

对于两个子空间\(S,T\)，若\(\forall \alpha \in S,\beta \in T,\alpha,\beta\)正交，则称这两个子空间是正交的，记作\(S\perp T\)。

对于矩阵\(A\)而言，显然\(C(A^T)\perp N(A)\)(行空间与零空间正交)，\(C(A)\perp N(A^T)\)(列空间与左零空间正交)

十五、子空间投影

1、向量投影

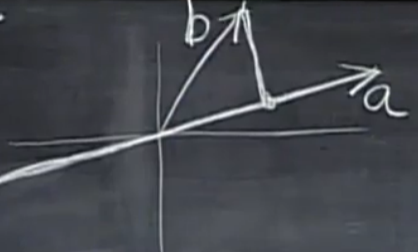
图中给出了一条直线(向量\(\alpha\)在该直线上)和另一向量\(\beta\)，求\(\beta\)在该直线(或者说向量\(\alpha\))上的投影向量\(p\)(向量\(\alpha,\beta,p\)均约定为列向量)

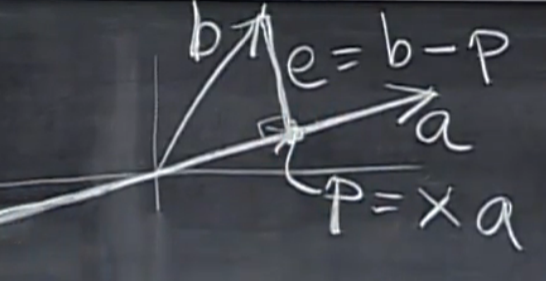
令误差向量\(e=\beta-p,e\perp \alpha\)，\(p=x\alpha\)(x是标量)则：

\(\alpha^Te=\alpha^T(\beta-p)=0\)，从而：

\(\alpha^T\beta=\alpha^Tp=x\alpha^T\alpha\)，于是得到

\[x=\frac{\alpha^T\beta}{\alpha^T\alpha} \]

• 显然\(p\)的模长与\(\alpha\)的模长无关。

那么\(p=x\alpha=\alpha x=\frac{\alpha\alpha^T\beta}{\alpha^T\alpha}=\frac{\alpha\alpha^T}{\alpha^T\alpha}\beta\)

令\(P=\frac{\alpha\alpha^T}{\alpha^T\alpha}\),称之为投影矩阵。

投影矩阵的性质：

• (1)\(P^T=P\),因为\(P^T=(\frac{\alpha\alpha^T}{\alpha^T\alpha})^T=\frac{1}{\alpha^T\alpha}(\alpha\alpha^T)^T=\frac{1}{\alpha^T\alpha}\alpha\alpha^T=P\)

• (2)\(P^2=P\),因为\(P^2=(\frac{\alpha\alpha^T}{\alpha^T\alpha})^2=(\frac{1}{\alpha^T\alpha})^2(\alpha\alpha^T)^2=(\frac{1}{\alpha^T\alpha})^2\alpha(\alpha^T\alpha)\alpha^T=(\frac{1}{\alpha^T\alpha})\alpha\alpha^T=P\)

2、向量在子空间上的投影

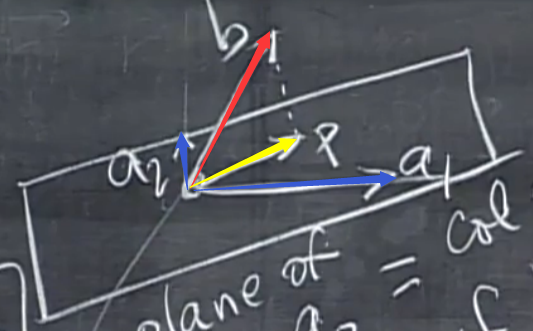
(以下的所有向量均为n维)
考虑向量\(b\)(图中红色向量)在二维子空间\(V\)上的投影\(p\)(图中黄色向量)，该子空间的一组基是\(\alpha_1,\alpha_2\)(图中蓝色向量)，\(p=\hat x_1\alpha_1+\hat x_2\alpha_2\)，令\(\hat X=\begin{pmatrix}\hat x_1\\ \hat x_2 \end{pmatrix}\)，\(A=\begin{pmatrix}\alpha_1 , \alpha_2 \end{pmatrix}\)，则\(p=A\hat X\)

令误差向量为\(e=\beta-p=\beta-A\hat X,e \perp V\)，则\(e\perp \alpha_1,e\perp \alpha_2\)，可得

\[\alpha_1^Te=\alpha_2^Te=0 \]

\[\begin{pmatrix} \alpha_1^T \\ \alpha_2^T\end{pmatrix}(\beta-A\hat X)=\begin{pmatrix} 0 \\ 0\end{pmatrix} \]

即：

\[A^T(\beta-A\hat X)=0 \]

显然\(e\in N(A^T)\)，而\(e \perp C((A^T)^T)=C(A)\)，这与第十四节课的内容相联系——A的左零空间正交于A的列空间

从而：

\[A^T\beta=A^TA\hat X \]

\[\hat X=(A^TA)^{-1}A^T\beta \]

\[p=A\hat X=A(A^TA)^{-1}A^T\beta \]

这里令投影矩阵\(P=A(A^TA)^{-1}A^T\)，当\(A\)为\(n\)阶方阵(即该子空间为\(\mathbb{R}^n\))时，显然\(P=I,p=P\beta=\beta\)，即\(\beta\)在n维空间下的投影就是n个自然基按\(\beta\)的坐标的线性组合

3、向量投影与最小二乘法之间的关系

对于非齐次线性方程组\(AX=b\)而言，其无解意味着\(b\neq C(A)\)，这时可以考虑将\(b\)投射到\(C(A)\)中得到\(\hat b\in C(A)\)，从而寻找近似解\(\hat X,A\hat X=\hat b\)，这样的\(\hat b\)是与\(b\)最接近的

给定二维空间中的若干个点\(p_i=(t_i,b_i)\)，最小二乘法可以拟合出一条直线\(b=C+Dt\)

一般来说，方程组

\[\begin{pmatrix} 1 & t_1 \\1 & t_2 \\\vdots & \vdots\\1 & t_m\end{pmatrix}\begin{pmatrix}C\\D\end{pmatrix}=\begin{pmatrix} b_1\\b_2 \\\vdots\\b_m\end{pmatrix} \]

是无解的，这就需要找到一组近似解\((\hat C,\hat D)\)。

最小二乘法的核心就是将等式右边的向量\(b\)投射到左边的系数矩阵的列空间中。

最小二乘法的目标是使找到的

\[\begin{pmatrix} 1 & t_1 \\1 & t_2 \\\vdots & \vdots\\1 & t_m\end{pmatrix}\begin{pmatrix}\hat C\\ \hat D\end{pmatrix}=\begin{pmatrix} \hat b_1\\\hat b_2 \\\vdots\\ \hat b_m\end{pmatrix}=\hat \beta \]

等式右边的向量与原始的

\[\beta=\begin{pmatrix} b_1\\b_2 \\\vdots\\b_m\end{pmatrix} \]

之间的距离最小，换言之

\[\mathrm{minimize}\ \ \sum_{i=1}^m(b_i-\hat b_i)^2 \]

而我们之前提到的\(\hat \beta\)是\(\beta\)在系数矩阵的列空间上的投影，在这个空间上，显然其他向量到\(\beta\)的距离都比\(\hat \beta\)大，所以这个\(\hat \beta\)是最优的。