Pymc边缘化离散变量实现DINA参数估计
https://www.yuque.com/xiaoqi-uhwyx/ueukvk/cr7whwyagm576z6q?singleDoc# 《Pymc边缘化离散变量实现DINA参数估计》
pymc使用NUTS算法,通常不能直接估计潜在变量,需要通过边缘化离散变量来实现参数估计。
具体理论可以参照stan教程:
https://mc-stan.org/users/documentation/case-studies/dina_independent.html
简单例子
比如学生类别\(\pi \sim Bern(0.3)\),第一个类别学生的作答正确概率为0.1\(P(Y=1|\pi=0)=0.1\),第二个类别的学生作答正确概率为0.8\(P(Y=1|\pi=1)=0.8\)。
不边缘化
如果观测结果为1,在不边缘化的情况下:
\(\pi\)的似然为\(0.3 \pi+ (1-0.3)(1-\pi)\)
\(Y\)的似然结果为:
- 如果\(\pi=0\), \(P(Y=1|\pi=0)=0.1\)。
- 如果\(\pi=1\), \(P(Y=1|\pi=1)=0.8\)。
边缘化
边缘化意味着我们要考虑\(\pi\)的所有情况对Y的似然影响,这可以通过以下方式实现:
\(P(Y)=[1-P(\pi)] P(Y=1|\pi=0)+P(\pi)P(Y=1|\pi=1)\\=0.7*0.1+0.3*0.8=0.31\)
通过这种方式,我们可以不对\(\pi\)的具体值进行采样,就可以计算边缘化版本的似然。这种方法在处理复杂模型或进行贝叶斯推断时特别有用,因为它可以显著减少计算的复杂度。
在CDM中
令\(\pi_{nc}\)为学生属于第c个类别的概率,学生n属于类别c时在第i题上作答正确概率为\(P(Y_{n_i}|\pi_{nc}=c)\),\(y_{ni}\)为观测数据。
则边缘化似然可以表示为
\(\Pr(Y_{ni}= y_{ni}) = \prod_{n=1}^N \left\{
\sum_{c=1}^C \pi_{nc} \left(
\prod_{i=1}^I \left[
P(Y_{ni}|\pi_{nc}=c)^{y_{ni}}
\left(1 - P(Y_{ni}|\pi_{nc}=c)\right)^{1-y_{ni}}
\right]
\right)
\right\}\)
令\(\Delta_{nic} = P(Y_{ni} | \pi_{nc} = c)^{y_{ni}} \cdot \left[ 1 - P(Y_{ni} | \pi_{nc} = c) \right]^{1 - y_{ni}}\)
\(Pr(Y_{ni}= {y_{ni}}) =\prod_{n=1}^N[\sum_{c=1}^C \pi_c \prod_{i=1}^I \Delta_{nic}]\)
在计算的时候我们通常计算对数似然以应对计算时的数值溢出,即logp
\(\begin{align}
\log L &= \log\left[\Pr(Y_{ni} = y_{ni})\right] \\
&= \log\left\{\prod_{n=1}^N\left[\sum_{c=1}^C \pi_c \prod_{i=1}^I \Delta_{nic}\right]\right\} \\
&= \sum_{n=1}^N \log\left[\sum_{c=1}^C \pi_c \prod_{i=1}^I \Delta_{nic}\right] \\
&= \sum_{n=1}^N \log\left[\sum_{c=1}^C \pi_c \; \exp\left(\sum_{i=1}^I \log (\Delta_{nic})\right)\right] \\
&= \sum_{n=1}^N \log\left[\sum_{c=1}^C \exp\left(\log(\pi_c)\right) \; \exp\left(\sum_{i=1}^I \log (\Delta_{nic})\right)\right] \\
&= \sum_{n=1}^N \log\left[\sum_{c=1}^C \; \exp\left(\log(\pi_c) + \sum_{i=1}^I \log (\Delta_{nic})\right)\right]
\end{align}\)
学生属于某一类别的概率可以通过后验得到
\(\begin{align}
P(\pi_{nc} = c) &= \frac{\pi_{nc} \prod_{i=1}^I \Delta_{nic}}{\sum_{c=1}^C \pi_{nc} \prod_{i=1}^I \Delta_{nic}} \\
&= \frac{\pi_{nc} \exp \left( \sum_{i=1}^I \log(\Delta_{nic}) \right)}{\sum_{c=1}^C \pi_{nc} \exp \left( \sum_{i=1}^I \log(\Delta_{nic}) \right)} \\
&= \frac{\exp(\log(\pi_{nc})) \exp \left( \sum_{i=1}^I \log(\Delta_{nic}) \right)}{\sum_{c=1}^C \exp(\log(\pi_{nc})) \exp \left( \sum_{i=1}^I \log(\Delta_{nic}) \right)} \\
&= \frac{\exp \left( \log(\Delta_{nic}) + \sum_{i=1}^I \log(\Delta_{nic}) \right)}{\sum_{c=1}^C \exp \left( \log(\Delta_{nic}) + \sum_{i=1}^I \log(\Delta_{nic}) \right)}
\end{align}\)
假设我们知道学生所有可能的属性掌握模型,为C行K(属性个数)列的矩阵\(\mathbf \Alpha\),则每个属性的掌握概率为
\(P(\Alpha_{ck}=1) = \sum_{c=1}^C P(\pi_{nc}=c) \Alpha_{ck}\)
Code
根据stan的教程和上述的公式,代码可写为:
其核心部分是似然的计算以及后验概率的计算
import pytensor
import pymc as pm
from pytensor import tensor as pt
import numpy as np
import itertools
import arviz as az
# 模拟参数生成
N = 500 # student count
I = 10 # item count
K = 3 # skill count
# all class
all_class = np.array(list(itertools.product(*[[0,1] for k in range(K)])))
# random sample from all possible class
class_idx = np.random.randint(0,len(all_class),size=N)
student_attribute = all_class[class_idx]
# Q-matrix
Q = np.concatenate([all_class[1:] for i in range(10)],axis=0)[:I]
# ideal response
eta = (student_attribute.reshape(N,1,K)>=Q.reshape(1,I,K)).prod(axis=-1)
s = np.random.uniform(0,0.3,(1,I))
g = np.random.uniform(0,0.3,(1,I))
Y = np.random.binomial(1,eta*(1-s-g)+g)
# 所有类别的理想作答
# ideal response for all classes
all_c_eta = (all_class.reshape(-1,1,K)>=Q.reshape(1,I,K)).prod(axis=-1)
all_c_eta = pt.as_tensor(all_c_eta)
with pm.Model() as DINA:
# 抽样学生属于某个类别的概率 pi_c
student_class_p = pm.Dirichlet("student_class_p", pt.ones(2**K), shape=( N, 2**K))
# 抽样题目参数
s_sample = pm.Beta("s",alpha=5,beta=25,shape=(1,I))
g_sample = pm.Beta("g",5,25,shape=(1,I))
# 每个类别在每个题目上对应的作答正确概率
# shape=C*I
all_c_p = pm.Deterministic("all_class_p",all_c_eta*(1-s_sample-g_sample)+g_sample)
# loglikelihood
logL_pY = pm.logp(pm.Bernoulli.dist(all_c_p.reshape((2**K,1,I))), Y.reshape((1,N,I))) # (C,N,I)
ps = pt.log(student_class_p) + logL_pY.sum(axis=-1).T
pm.Potential("logL", pt.log(pt.exp(ps).sum(axis=-1)))
# 计算类别和属性掌握后验概率
prob_resp_class = pm.Deterministic("prob_resp_class",pt.exp(ps)/pt.exp(ps).sum(axis=-1, keepdims=True))
pm.Deterministic("att_p", prob_resp_class.dot(all_class))
with DINA:
tr = pm.sample(1000,tune=3000,chains=2,return_inferencedata=True)
可以得到结果
题目参数估计
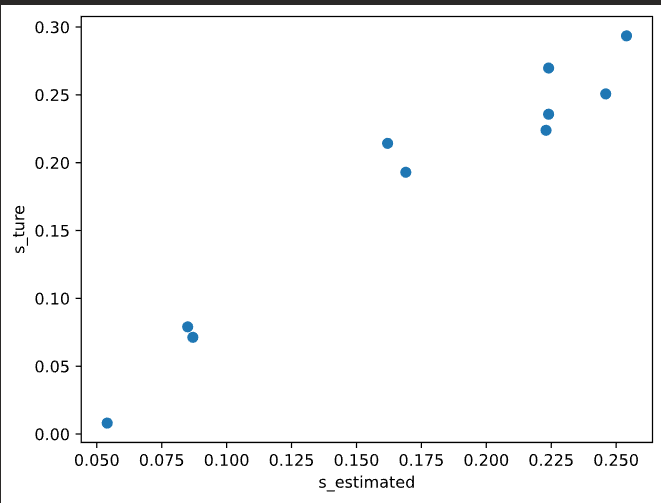
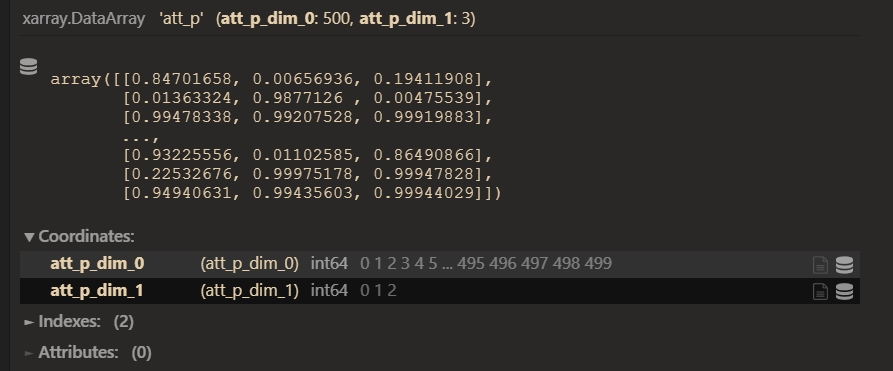
学生属性掌握后验概率



 浙公网安备 33010602011771号
浙公网安备 33010602011771号