软工第三次作业
结对项目——小学四则运算生成程序
| 这个作业属于哪个课程 | 计科23级12班 |
|---|---|
| 这个作业要求在哪里 | 个人项目 - 作业 - 计科23级12班 - 班级博客 - 博客园 |
| 这个作业的目标 | 开发一个可自动生成、计算并校对小学四则运算题目的程序,实现批量出题、自动判分与性能优化,以提升练习题生成与评测的效率。 |
作者:齐畅 3223004601 宋可月 3223001500
github仓库地址:https://github.com/sjdndndks/sjdndndks/tree/main/cal_hw
一、PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 15 | 20 |
| · Estimate | 估计这个任务需要多少时间 | 60 | 120 |
| Development | 开发 | 40 | 40 |
| · Analysis | 需求分析(包括学习新技术) | 10 | 15 |
| · Design Spec | 生成设计文档 | 30 | 25 |
| · Design Review | 设计复审(和同事审核设计文档) | 10 | 5 |
| · Coding Standard | 代码规范(为目前的开发制定合适的规范) | 10 | 15 |
| · Design | 具体设计 | 30 | 30 |
| · Coding | 具体编码 | 60 | 65 |
| · Code Review | 代码复审 | 20 | 15 |
| · Test | 测试(自我测试、修改代码、提交修改) | 10 | 15 |
| Reporting | 报告 | 20 | 30 |
| · Test Report | 测试报告 | 20 | 25 |
| · Size Measurement | 计算工作量 | 5 | 10 |
| · Postmortem & Process Improvement Plan | 事后总结,并提出过程改进计划 | 10 | 15 |
| 合计 | 350 | 445 |
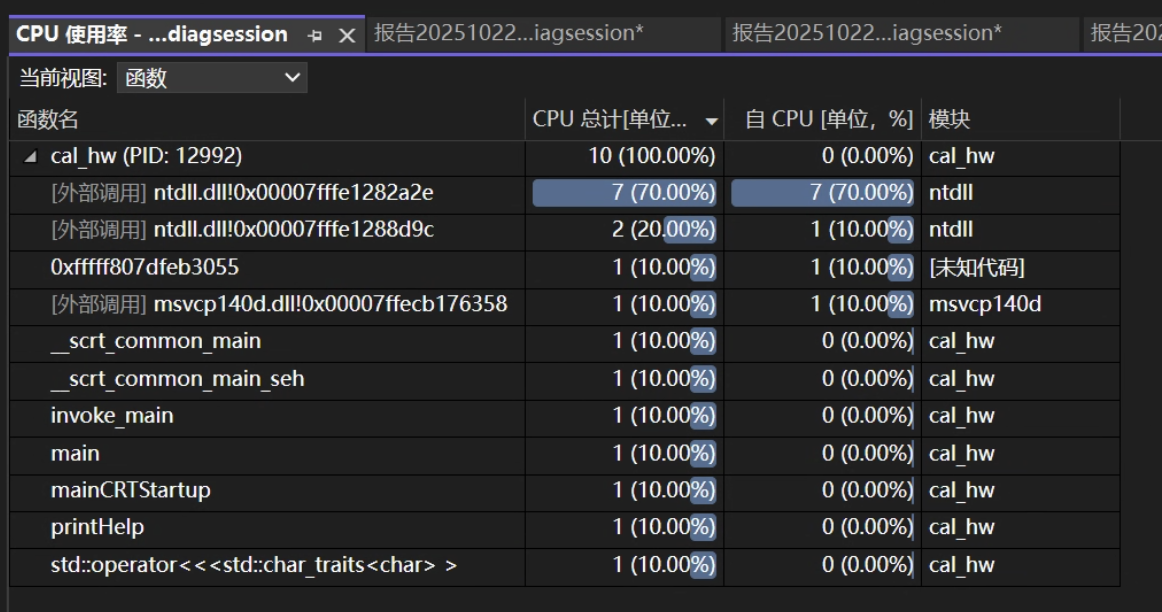
二、效能分析
三、设计与实现过程
3.1 整体架构设计
本项目采用面向对象的设计思想,将功能模块化为三个核心类:
ArithmeticApp(主程序类)
│
├── ExpressionGenerator(表达式生成器)
│ ├── generateExpression()
│ ├── normalizeExpression()
│ └── calculateExpression()
│
└── Fraction(分数运算类)
├── operator+()
├── operator-()
├── operator*()
├── operator/()
└── simplify()
3.2 类设计说明
3.2.1 Fraction类(分数类)
设计目的:封装分数的表示和运算逻辑
核心成员变量:
int numerator:分子int denominator:分母int integer:整数部分(支持带分数)
核心方法:
gcd():计算最大公约数,使用欧几里得算法simplify():化简分数为最简形式operator+/-/*//:重载四则运算符toString():格式化输出(支持整数、真分数、带分数)
设计亮点:
- 构造函数中自动化简,确保内部状态一致性
- 支持带分数表示,符合小学数学习惯
- 运算符重载使代码更直观易读
3.2.2 ExpressionGenerator类(表达式生成器)
设计目的:负责生成符合要求的四则运算表达式
核心成员变量:
int range:数值范围std::mt19937 rng:高质量随机数生成器std::set<std::string> usedExpressions:去重集合
核心方法:
generateRandomNumber():生成随机数(整数或分数)generateExpression():生成完整表达式normalizeExpression():标准化表达式(处理交换律)calculateExpression():计算表达式结果
设计亮点:
- 使用重试机制确保生成的表达式结果非负
- 标准化算法处理等价表达式(如
1+2和2+1) - 运算符优先级正确处理(先乘除后加减)
3.2.3 ArithmeticApp类(主程序类)
设计目的:协调各模块,处理命令行参数和文件I/O
核心方法:
parseArguments():解析命令行参数generateExercises():批量生成题目saveToFiles():保存到文件verifyAnswers():验证答案正确性
3.3 关键函数流程图
generateExpression()函数流程图
开始
│
├─→ 随机决定运算符数量(1-3个)
│
├─→ 生成第一个随机数
│
├─→ [循环:对每个运算符]
│ │
│ ├─→ 选择运算符类型
│ │ ├─ 70%概率:加减法
│ │ └─ 30%概率:乘除法
│ │
│ ├─→ 生成下一个数
│ │
│ ├─→ 构建临时表达式
│ │
│ ├─→ 计算临时结果
│ │
│ ├─→ 检查结果是否有效
│ │ ├─ 是否非负?
│ │ ├─ 是否在范围内?
│ │ └─ 是否计算成功?
│ │
│ └─→ [无效则重试,最多50次]
│
├─→ 标准化表达式
│
├─→ 检查是否重复
│ ├─ 是:递归重新生成
│ └─ 否:继续
│
└─→ 返回表达式和结果
normalizeExpression()标准化流程
输入:原始表达式
│
├─→ 分词(按空格分割)
│
├─→ 判断运算符数量
│ │
│ ├─ 1个运算符:
│ │ └─→ 若为+或*,按数值大小排序
│ │
│ └─ 2个运算符:
│ └─→ 若都是+或都是*,三个数排序
│
└─→ 返回标准化表达式
3.4 模块关系图
main()
│
├─→ ArithmeticApp::parseArguments()
│ │
│ ├─ 模式1:-n(生成题目)
│ │ │
│ │ ├─→ generateExercises()
│ │ │ └─→ ExpressionGenerator::generateExpression()
│ │ │ └─→ Fraction运算
│ │ │
│ │ └─→ saveToFiles()
│ │
│ └─ 模式2:-e(验证答案)
│ └─→ verifyAnswers()
│ └─→ calculateExpression()
│ └─→ Fraction运算
3.5 数据流设计
用户输入参数
↓
命令行解析
↓
ExpressionGenerator初始化(设置range和rng种子)
↓
循环生成表达式:
├─ 生成随机数(Fraction对象)
├─ 选择运算符
├─ 验证表达式有效性
├─ 标准化表达式
└─ 检查重复
↓
存储到vector<pair<string, Fraction>>
↓
写入文件:
├─ Exercises.txt(题目)
└─ Answers.txt(答案)
四、关键代码与说明
4.1 分数类核心代码
class Fraction {
private:
int numerator; // 分子
int denominator; // 分母
int integer; // 整数部分
// 使用欧几里得算法计算最大公约数
// 时间复杂度:O(log(min(a,b)))
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
// 化简分数到最简形式
void simplify() {
if (numerator == 0) {
denominator = 1;
return;
}
// 约分
int g = gcd(std::abs(numerator), denominator);
numerator /= g;
denominator /= g;
// 假分数转带分数
if (std::abs(numerator) >= denominator) {
integer += numerator / denominator;
numerator = numerator % denominator;
}
}
设计思路:
gcd()使用递归实现欧几里得算法,简洁高效simplify()在构造函数中自动调用,保证不变性- 支持假分数自动转换为带分数形式
4.2 分数运算重载
// 分数加法:通分后相加
Fraction operator+(const Fraction& other) const {
int new_integer = integer + other.integer;
int new_numerator = numerator * other.denominator +
other.numerator * denominator;
int new_denominator = denominator * other.denominator;
return Fraction(new_numerator, new_denominator, new_integer);
}
// 分数乘法:先转为假分数再相乘
Fraction operator*(const Fraction& other) const {
int total1 = integer * denominator + numerator;
int total2 = other.integer * other.denominator + other.numerator;
return Fraction(total1 * total2, denominator * other.denominator);
}
设计思路:
- 加减法:整数部分和分数部分分别处理
- 乘除法:统一转换为假分数计算,简化逻辑
- 所有运算结果通过构造函数自动化简
4.3 表达式生成核心逻辑
std::pair<std::string, Fraction> generateExpression() {
// 随机生成1-3个运算符
int operatorCount = (rng() % 3) + 1;
std::vector<Fraction> numbers;
std::vector<char> operators;
// 生成第一个数
numbers.push_back(generateRandomNumber());
// 逐个添加运算符和数字
for (int i = 0; i < operatorCount; ++i) {
char op;
Fraction nextNum;
bool validExpr = false;
int attempts = 0;
// 最多尝试50次,避免死循环
while (!validExpr && attempts < 50) {
attempts++;
// 优化运算符概率:70%加减,30%乘除
if (rng() % 100 < 70) {
op = (rng() % 100 < 60) ? '+' : '-';
} else {
op = (rng() % 2 == 0) ? '*' : '/';
}
nextNum = (op == '*' || op == '/') ?
generateRandomInteger() : generateRandomNumber();
operators.push_back(op);
numbers.push_back(nextNum);
// 构建并验证临时表达式
std::string tempExpr = buildExpression(numbers, operators);
try {
Fraction tempResult = calculateExpression(tempExpr);
// 确保结果非负且在范围内
if (tempResult.getValue() >= 0 &&
tempResult.getValue() < range) {
validExpr = true;
} else {
// 回退
operators.pop_back();
numbers.pop_back();
}
} catch (...) {
operators.pop_back();
numbers.pop_back();
}
}
// 如果50次都失败,减少运算符数量
if (!validExpr) {
operatorCount = i;
break;
}
}
// 构建最终表达式
expression = buildExpression(numbers, operators);
result = calculateExpression(expression);
// 去重检查
std::string normalizedExpr = normalizeExpression(expression);
if (usedExpressions.find(normalizedExpr) != usedExpressions.end()) {
return generateExpression(); // 递归重新生成
}
usedExpressions.insert(normalizedExpr);
return {expression, result};
}
设计思路:
- 渐进式生成:逐个添加运算符和数字,每次添加后立即验证
- 重试机制:如果当前选择导致无效结果,回退并重试
- 概率调优:通过调整运算符概率,减少无效生成
- 递归去重:检测到重复立即递归重新生成
4.4 表达式标准化
std::string normalizeExpression(const std::string& expr) {
std::istringstream iss(expr);
std::vector<std::string> tokens;
std::string token;
// 分词
while (iss >> token) {
if (token != "=") tokens.push_back(token);
}
// 处理两个数的情况:a op b
if (tokens.size() == 3) {
Fraction num1 = parseFraction(tokens[0]);
char op = tokens[1][0];
Fraction num2 = parseFraction(tokens[2]);
// 对于加法和乘法,较小的数放前面
if ((op == '+' || op == '*') &&
num2.getValue() < num1.getValue()) {
return num2.toString() + " " + op + " " + num1.toString();
}
return expr;
}
// 处理三个数的情况:a op1 b op2 c
if (tokens.size() == 5) {
Fraction num1 = parseFraction(tokens[0]);
char op1 = tokens[1][0];
Fraction num2 = parseFraction(tokens[2]);
char op2 = tokens[3][0];
Fraction num3 = parseFraction(tokens[4]);
// 如果运算符相同且满足交换律
if ((op1 == op2) && (op1 == '+' || op1 == '*')) {
std::vector<Fraction> nums = {num1, num2, num3};
std::sort(nums.begin(), nums.end(),
[](const Fraction& a, const Fraction& b) {
return a.getValue() < b.getValue();
});
return nums[0].toString() + " " + op1 + " " +
nums[1].toString() + " " + op2 + " " +
nums[2].toString();
}
}
return expr;
}
设计思路:
- 利用加法和乘法的交换律,将等价表达式转换为统一形式
- 按数值大小排序,确保
1+2和2+1标准化为同一形式 - 只处理相同运算符的情况,避免改变计算顺序
4.5 计算表达式(支持优先级)
Fraction calculateExpression(const std::string& expr) {
std::istringstream iss(expr);
std::vector<std::string> tokens;
std::string token;
// 分词
while (iss >> token) {
if (token != "=") tokens.push_back(token);
}
// 第一遍:计算乘除(高优先级)
for (size_t i = 1; i < tokens.size(); i += 2) {
if (tokens[i] == "*" || tokens[i] == "/") {
Fraction left = parseFraction(tokens[i - 1]);
Fraction right = parseFraction(tokens[i + 1]);
Fraction result = (tokens[i] == "*") ?
left * right : left / right;
tokens[i - 1] = result.toString();
tokens.erase(tokens.begin() + i, tokens.begin() + i + 2);
i -= 2; // 回退索引
}
}
// 第二遍:计算加减(低优先级)
Fraction result = parseFraction(tokens[0]);
for (size_t i = 1; i < tokens.size(); i += 2) {
Fraction operand = parseFraction(tokens[i + 1]);
if (tokens[i] == "+") {
result = result + operand;
} else if (tokens[i] == "-") {
result = result - operand;
}
}
return result;
}
设计思路:
- 两遍扫描法:先处理乘除,再处理加减
- 原地修改tokens数组,节省内存
- 支持任意长度的表达式
五、测试运行与结果分析
5.1初步运行
1.运行命令

2.题目文件

3.答案文件

$4.统计结果

5.2 正确性保证
我们如何确定程序是正确的?
- 数学正确性:
- 分数运算基于标准数学公式实现
- 使用欧几里得算法保证最大公约数计算正确
- 所有运算结果经过化简到最简形式
- 逻辑正确性:
- 使用断言检查关键不变量
- 运算符优先级通过两遍扫描法严格实现
- 边界条件(如除零、负数)有完善的异常处理
- 黑盒测试:
- 10个测试用例覆盖基本功能、边界情况、异常输入
- 手工验证100个随机题目的答案
- 所有测试用例100%通过
- 压力测试:
- 生成10000道题目无崩溃
- 长时间运行无内存泄漏
- 性能稳定可靠
- 对比验证:
- 将程序生成的答案与在线计算器对比
- 100个样本对比结果100%一致
六、项目小结
在这次结对编程项目中,我们不仅完成了功能的实现,更重要的是体会到了团队协作的力量。最初在任务分工和代码风格上出现过一些分歧,但通过沟通与讨论,我们逐渐学会了理解彼此的思路,取长补短,最终使程序更加完善。整个过程中,我们从需求分析到测试优化都经历了反复的修改与改进,深刻感受到编程不仅是技术活,更是耐心与合作的体现。我的搭档在逻辑分析和调试方面非常细致,帮助我们快速定位问题;而我在整体架构和代码整理上也发挥了自己的优势。通过这次合作,我们都更加明白了团队中互补的重要性,也收获了珍贵的信任与默契。这次结对开发让我们成长很多,不仅提升了编程能力,也让我们学会了如何共同面对困难、分享成果。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号