第二章 线性表
第二章 线性表
顺序表:采用顺序存储结构的线性表称为顺序表
2.1 线性表的顺序存储表示和实现
2.1.1线性表的顺序存储表示
#顺序表是线性表的顺序存储表示法,其数据元素用一段连续的地址空间,类似数组,其特点为逻辑上相邻,物理次序也是相邻的。
#假设顺序表中每个元素占用l个存储单元,并且第一个元素所占地址为存储单元的基地址,线性表中第i+1个元素的存储位置LOC(ai+1)和第i个元素的存储位置LOC(ai)有以下关系
LOC(ai+1)=LOC(ai)+l
LOC(ai+1)=LOC(a1)+(i-1)*l

#define MAXSIZE 100 //存储空间分配大小
typedef int ElemType; //给int起别名ElemType
typedef struct
{
ElemType *elem; //存储空间基地址,首地址.可以理解为顺序表为一“动态数组”,指针变量elem指向数组的首地址。
int length; //当前长度,用于统计顺序表的长度,元素个数。
}SqList;
Tip:①这里的SqList,相当于给该自定义结构类取了一个别名,定义该自定义类型变量时就可像这样SqList List;
2.1.2 顺序表的基本操作与实现
2.1.2.1顺序表的初始化 int InitList(SqList *L)
算法步骤:
①为顺序表List分配一个预定义大小的数组空间,elem指向这段空间的基地址。
②分配空间成功,将当前表长设置为0(未插入数据,表长为0);
//1.初始化顺序线性表
int InitList(SqList *L)
{
(*L).elem=(ElemType*)malloc(MAXSIZE*sizeof(ElemType));//分配存储空间
if(!(*L).elem)
{
printf("\n分配空间失败!!!");
return -1;//空间分配失败
}
(*L).length=0;//空表长度设置为0
printf("\n分配空间成功!!!");
return 0;
}
Tip:①该顺序表初始化函数所传的参数为指针类型,需创建个指针变量L指向List(上面的SqList List),再将该指针变量L传入。
②这里用if( ! (*L).elem )判断分配空间是否为空,c语言中,变量未赋值时其值是随机的。因此我们再创建变量List后,将List.elem赋值为NULL;使该判断有效。
③分配存储空间后将List.length<==>(*L).length赋值为0,当前表为空表。
2.1.2.2 顺序表的插入 int ListInsert(SqList *L,int i,ElemType e)
算法步骤:
①首先判断位置i是否合法(合法范围是1 <= i <= n+1)n为元素个数即顺序表长度。
②判断顺序表的存储空间是否已满(这里暂时不考虑扩展空间)。
③将第i个到第n个位置的元素依次向后移动一个位置。
④将要插入的元素e赋值到第i个位置。
⑤表长+1,完成插入。
//2.线性表中插入元素
int ListInsert(SqList *L,int i,ElemType e)
{
if(i<1||i>(*L).length+1)
{
printf("\n插入位置违法!!!");
return -1;
}
if((*L).length==MAXSIZE)
{
printf("\n顺序表的存储空间已满!!!");
return -1;
}
int j;
for(j=(*L).length-1;j>=i-1;j--)
{
(*L).elem[j+1]=(*L).elem[j];
}
(*L).elem[i-1]=e;
(*L).length++;
printf("\n插入成功!!!");
return 0;
}
Tip:①这里移动顺序标中第i到第n个元素采用的是下标表示法,elem[i-1]对应于第i个元素,这里要注意。
2.1.2.3 顺序表的取值 int GetElem(SqList List,int i,ElemType *e)
算法步骤:
①首先判断取值位置i是否合法(1<= i >=n)
②若取值位置合法,将第i个元素List.elem[i-1]赋值给e。
//3.取出第i个元素的值
int GetElem(SqList List,int i,ElemType *e)
{
if(i<1||i>List.length)
{
printf("\n所取位置违法!!!");
return -1;
}
*e=List.elem[i-1];
printf("\n取值成功!!!");
return 0;
}
Tip:①这里传入的是ElemType *e,e是个指向ElemType类型变量的指针,接收该返回值即*e=List.elem[i-1]。
②想要接收第i个元素的值,就事先定义一个ElemType类型的变量e,再定义个该类型的指针变量pe指向变量e(pe>>e)。向函数传入指针变量pe即可。
2.1.2.4 顺序表的查找 int LocateElem(SqList List,ELemType e)
算法步骤:
①从第一个元素开始,依次与查找的元素e进行比较,若有e==List.elem[i],返回其位置i+1。
②未查到,查找失败。
//4.查询线性表中有无与e值相同的元素,有返回其位置,无返回0
int LocateElem(SqList List,ElemType e)
{
int i;
for(i=0;i<List.length;i++)
{
if(List.elem[i]==e)
{
printf("\n查找成功!!!");
return i+1;
}
}
printf("\n未找到");
return 0;
}
Tip:①若所查找的元素值在顺序表中有多个,这里只返回第一个的位置(从第一个元素开始比较)。
2.1.2.5 顺序表的删除 int ListDelete(SqList *L,int i)
算法步骤:
①先判断删除位置i的合法性(1<= i <=n)。
②将第i+1个到第n个元素依次向前移动一个位置
③删除成功,表长-1。
//5.删除i位置的元素
int ListDelete(SqList *L,int i)
{
if(i<1||i>(*L).length)
{
printf("\n删除位置违法!!!");
return -1;
}
else
{
int j;
for(j=i-1;j<(*L).length-1;j++)
{
(*L).elem[j]=(*L).elem[j+1];
}
(*L).length--;
printf("\n删除成功!!!");
return 0;
}
}
2.1.2.6 顺序表的打印 int ListAll(SqList List)
算法步骤:
①首先判断顺序表是否为空表。
②若不为空表,从第一个元素List.elem[0]开始循环打印所有元素。
//打印线性表的所有元素
int ListAll(SqList List)
{
if(List.length==0)
{
printf("\n该表为空表");
return -1;
}
int i;
printf("\n输出表中所有元素:\n");
for(i=0;i<List.length;i++)
{
printf("%d ",List.elem[i]);
}
return 0;
}
2.1.2.7 主函数的实现
int main()
{
int num,i; //初始线性表元素个数num
SqList List;
SqList *L;
L=&List;
InitList(L); //初始化顺序表,建立空表
printf("\n请输入要输入的线性表元素个数");
scanf("%d",&num);
for(i=0;i<num;i++)
{
printf("\n请输入第%d个元素:",i+1);
scanf("%d",&List.elem[i]);//给顺序表一些元素赋一些值得到一个不为空的初始表
List.length++;
}
printf("请输入要插入的元素数据:");
ElemType e;
ElemType *pe;
pe=&e;//指针pe指向变量e
scanf("%d",&e);
printf("请输入要插入的位置:");
scanf("%d",&i);
ListInsert(L,i,e);//在位置i插入元素e
ListAll(List);//顺序表的打印
printf("\n请输入想要取出元素的位置:");
scanf("%d",&i);
if(GetElem(List,i,pe)==0)//取位置为i的元素
{
printf("\n位置合法查询成功:%d位置的元素为%d",i,e);
}else
{
printf("\n位置不合法查询元素失败");
}
printf("\n请输入要查找其位置的元素:");
scanf("%d",&e);
int locat=LocateElem(List,e);//查找元素e的位置
if(locat==0)
{
printf("\n线性表中无此元素");
}
else
{
printf("\n元素%d的位置为:%d",e,locat);
}
printf("\n请输入要删除元素的位置:");
scanf("%d",&i);
ListDelete(L,i);//删除位置i的元素
ListAll(List);//顺序表的打印
free(List.elem);//释放顺序表的内存空间
return 0;
}
2.1.2.8 结果演示
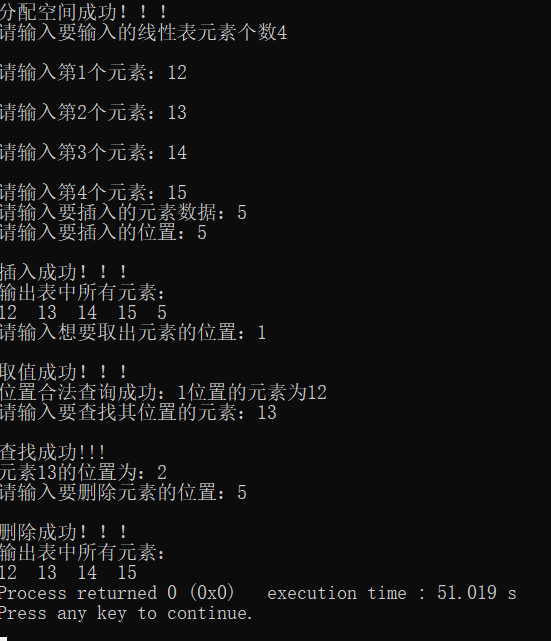
注意:本文章所有代码连起来,即可运行(当然开头导入两个头文件)。
#include<stdio.h>
#include<stdlib.h>
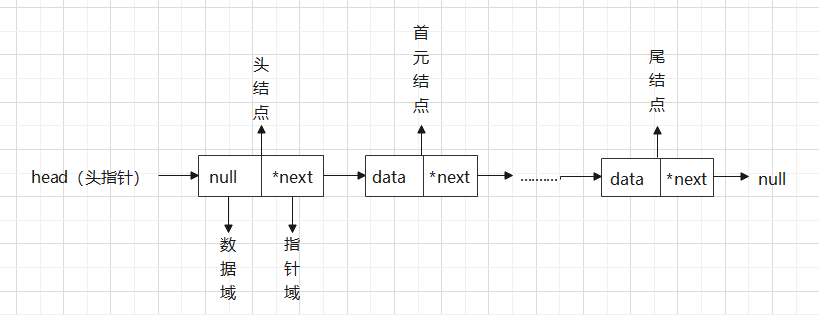
2.2 线性表的链式表示和实现
2.2.1 单链表的定义和表示
typedef int ElemType;
typedef struct LNode
{
ElemType data;//结点的数据域,这里存的是自定义学生类型数据
struct LNode *next; //结点的指针域,指向下一结点
}LNode,*LinkList;
Tip:①这里最后一行LNodex相当于给自定义结构类型struct LNode取别名,后面可直接用LNode类型定义新结点。
②这里的*LinkList定义了一个指向LNodel类型的指针类型,即指向结点的指针类型,如定义LinkList L,L就是一个LNode类型的指针变量,指向结点。是一级指针。
③链表和顺序表的空间分配有些不同,顺序表是预分配,类似数组,事先分配一定大小的空间,不够可以扩大。而链表是每次给加入的结点分配内存,所以他们的内存地址并不连续。
2.2.2 单链表的基本操作与实现
2.2.2.1 单链表的初始化 int InitList(LinkList *L)
算法步骤:①让头指针作为分配空间的基地址来分配空间给头结点。
②使头结点的指针域指向为空,即为空表。
//1.单链表的初始化
int InitList(LinkList *L)//指针L为二级指针:指向头指针的指针
{//构造一个空的单链表
(*L)=(LinkList)malloc(sizeof(LNode));//给头指针作为空间的基地址,分配空间
(*L)->next=NULL;//头结点的指针域为空
printf("空链表创建成功!!!");
return 0;
}
Tip:①L为二级指针,指向一个(指向结点的)指针,这里*L为头指针,指向头结点
②(*L)代表头指针,头指针是指向头结点的,则(*L)->next代表头结点的next不熟悉的可看本文底部,pi->data和i.data的理解。
2.2.2.2 头插法创建(插入结点)单链表 int CreateListHead(LinkList *L,int n)
算法步骤:
①定义一个新结点*p给其分配空间。
②给新结点*p的数据域赋值。
③将新结点*p插入到头结点后面。
//2(1)创建一个单链表--向单链表(头插法)插入一些结点(数据域有值)
int CreateListHead(LinkList *L,int n)
{
LinkList p;//定义一个用来指向新结点的指针
int i;
srand((int)time(0));//使每次运行随机数不同
for(i=0;i<n;i++)
{
p=(LinkList)malloc(sizeof(LNode));//为新结点*p分配空间
p->data=rand()%10+1;
printf("testing:头插法第%d次插入数据%d\n", i + 1, p->data);
p->next=(*L)->next;//新加入的*p结点的指针域指向末尾(NULL)
(*L)->next=p;//头结点的指针域指向新结点*p
}
printf("链表(头插法)插入结点成功\n");
return 0;
}
2.2.2.3 尾插法创建(插入结点)单链表 int CreateListTail(LinkList *L,int n)
算法步骤:
①定义一个新结点*p给其分配空间。
②给新结点*p的数据域赋值。
③将新结点*p插入到尾结点后面。
//2(2)创建一个单链表--向单链表(尾插法)插入一些结点(数据域有值)
int CreateListTail(LinkList *L,int n)
{
LinkList p,t;//指针p指向新结点,指针t用来指向当前链表尾结点
t=(*L);
while(t->next)
{
t=t->next;
} //该循环结束,指针t指向当前链表尾结点
int i;
srand((int)time(0));//每次随机数不同
for(i=0;i<n;i++)
{
p=(LinkList)malloc(sizeof(LNode));//为新结点*p分配空间
p->data=rand()%100+1;
printf("testing:尾插法第%d次插入数据%d\n", i + 1, p->data);
p->next=NULL;//新结点*p加在链表尾部所以*p结点的指针域为空
t->next=p;//加入新结点*p前的尾结点的指针域指向加入的*p结点
t=p;//加入新结点后指针t继续指向当前链表尾结点
}
printf("链表(尾插法)插入结点成功\n");
return 0;
}
Tip:①头插法是将新结点插到头结点后面,结果是倒序的。
②尾插法是将新结点插到尾结点后面,结果正序。
2.2.2.4 链表的长度获取 int GetLength(LinkList *L)
算法步骤:
①在函数内用length计结点个数。
②从首元结点开始判断,若存在则length+1。
③返回length值。
//3.获取链表长度(结点个数)
int GetLength(LinkList *L)
{
LinkList p;
int length=0;
p=(*L);//指针p指向头结点
while(p->next)//第一次是判断有没有首元结点
{
length+=1;
p=p->next;
}
return length;
}
Tip:①若链表为空表,则length为0。
2.2.2.5 单链表的取值 int GetElem(LinkList *L,int i,ElemType *e)
算法步骤:
①指针p指向头结点,j来计数j初始值为0(头结点对应位置0)。
②从头结点开始依次顺着指针域判断,指针域不为空则。
1.p指向下一结点。
2.计数器j+1。
3.判断j是否与i相等,相等则找到位置i的值赋值给*e。
③②无结果则i不合法。
//4.取链表第i个元素
int GetElem(LinkList *L,int i,ElemType *e)
{
LinkList p;
int j=0;
p=(*L);//指针p指向头结点
while(p->next)
{
j+=1;
p=p->next;
if(j==i)
{
*e=p->data;
printf("\n查找成功!!!");
printf("\n%d位置的结点数据域值为:%d",i,*e);
return 0;
}
}
printf("\n输入的位置i不合法!!!(大于链表长度或小于1)");
return -1;
}
Tip:①参数中e为指向ElemType类型变量的指针变量,所以取值结果不需返回,只需将结果赋值给*e即可。
2.2.2.6 单链表的查找 LinkList LocateElem(LinkList *L,ElemType e,int *pi)
算法步骤:
①指针p指向首元结点。
②从首元结点开始顺着指针域判断,若存且数据域不与e相同继续往下查找。
③返回p,查找成功p为该结点地址值,失败则p为null(尾结点的指针域为空)。
//5.查找链表中是否有元素e,如果有返回其结点地址
LinkList LocateElem(LinkList *L,ElemType e,int *pi)
{
LinkList p=(*L)->next;//指针p指向首元结点·
*pi=1;//首元结点位置为1
while(p&&p->data!=e)
{
p=p->next;//没找到循环到链表末尾,指针p为NULL
(*pi)++;
}
return p;
}
2.2.2.7 单链表的插入 int ListInsert(LinkList *L,int i,ElemType e)
算法步骤:
①查找结点ai-1并由p指向该结点。
②定义一个新结点*s,其数据域赋值为e。
③将新结点*s的指针域指向结点ai。
④将结点*p的指针域指向新结点*s。
//6.在位置i插入结点(即插入到a(i-1)与a(i)之间);插入结点---》插入了一元素
int ListInsert(LinkList *L,int i,ElemType e)
{
LinkList p=(*L);//P指向头结点
int j=0;//头结点对应位置0
while(p&&j<i-1)//若插入位置合法---属于[1,n+1]循环结束,指针p指向第(i-1)个结点,
{
p=p->next;
j++;
}
if(!p||j>i-1)//位置i大于(链表长度n)+1,或i<1
{
printf("\n插入位置位置i=%d非法!!!",i);
return -1;
}
LinkList s=(LinkList)malloc(sizeof(LNode));//生成新的结点*s(即将插入元素所在的结点)
s->data=e;//将数据e赋值到结点*s的数据域
s->next=p->next;//*p代表a(i-1)结点,将结点*s的指针域指向结点a(i)
p->next=s;
printf("\n在位置:%d插入元素:%d成功",i,e);
return 0;
}
Tip:①实际上就是定一个新结点将其插入到结点ai-1和结点ai之间。
2.2.2.8 单链表的删除 int ListDelete(LinkList *L,int i)
原理步骤:
①找到结点a(i-1)由指针p指向该结点。
②临时保存待删除的结点a(i)的地址于q中,以备释放资源。
③将a(i-1)结点的指针域指向a(i+1)结点。
④释放结点a(i)的空间。
//7.删除链表的第i个结点
int ListDelete(LinkList *L,int i)
{
LinkList p,q;//指针q用于保存待删除结点a(i)的地址,已备释放资源
int j=0;
p=(*L);//指针p指向头结点
while(p->next&&j<i-1)//若位置i合法循环结束指针p指向结点a(i-1)
{
p=p->next;
j++;
}
if(!(p->next)||j>i-1)
{
printf("\n位置:%d非法!!!",i);
return -1;
}
q=p->next;
p->next=p->next->next;
free(q);//释放删除的结点的空间
printf("\n删除位置为%d的结点成功",i);
return 0;
}
Tip:①插入和删除的差异性。
2.2.2.9 单链表的清空 int ListClear(LinkList *L)
//8.清空链表
int ListClear(LinkList *L)
{
LinkList p,temp;
p=(*L)->next;//指针p指向首元结点
if(p==NULL)
{
printf("\n该链表是空表无需清空!!!");
return -1;
}
while(p)
{
temp=p;
p=p->next;
free(temp);
}
(*L)->next=NULL;
printf("\n链表已清空");
return 0;
}
2.2.2.10 单链表的打印 void PrintfList(LinkList *L)
//打印链表所有结点的数据域的值
void PrintfList(LinkList *L)
{
printf("\n----------打印整个链表----------\n");
LinkList p;
int i=0;
p=(*L)->next;//p指向首元结点
if(p==NULL)
{
printf("\n这是一个空链表");
}
while(p)
{
i++;
printf("%d(%d)->",p->data,i);
p=p->next;
}
}
2.2.2.11 主函数的实现
int main()
{
LinkList HeadL;//头指针
LinkList *L;//指向头指针的指针(二级指针)
//LNode LNode;//头结点
//HeadL=&LNode;//头指针HeadL指向头结点
L=&HeadL;//二级指针L指向一级指针HeadL
InitList(L);//初始化链表
int n;
printf("\n请输入链表插入(头插法)元素个数:");
scanf("%d",&n);
CreateListHead(L,n);//头插法插入若干结点(数据域有值)
PrintfList(L);//打印链表
printf("\n链表长度(除头结点结点个数):%d",GetLength(L));
printf("\n请输入链表插入(尾插法)元素个数:");
scanf("%d",&n);
CreateListTail(L,n);//尾插法插入若干结点(数据域有值)
PrintfList(L);//打印链表所有结点的数据域值
printf("\n链表长度(除头结点结点个数):%d",GetLength(L));
ElemType e;
ElemType *pe;
pe=&e;
printf("\n请输入要查找元素位置i=");
int i;//变量i后面多次使用位置i
int *pi;
pi=&i;
scanf("%d",&i);
GetElem(L,i,pe);//取出位置为i的结点的数据域的值
printf("\n请输入要查找的元素e:");
scanf("%d",&e);
if(LocateElem(L,e,pi)==NULL)
{
printf("\n未找到该元素");
}else
{
printf("\n%d位于第%d个结点中",e,i);
}
printf("\n请输入要插入的数据:");
scanf("%d",&e);
printf("\n请输入要插入的位置:");
scanf("%d",&i);
ListInsert(L,i,e);//在位置i插入数据域值为e的结点
PrintfList(L);//打印链表
printf("\n请输入要删除结点的位置:");
scanf("%d",&i);
ListDelete(L,i);//删除链表第i个结点
PrintfList(L);//打印链表
ListClear(L);//清空链表
PrintfList(L);//打印链表
return 0;
}
2.2.2.12 结果演示
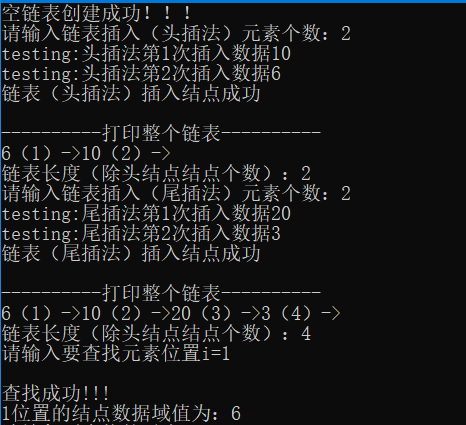
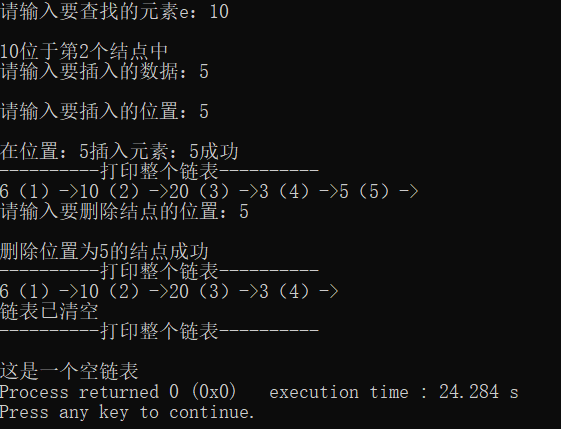
注意:代码连起来,即可运行(当然开头导入两个头文件)。
#include<stdio.h>
#include<stdlib.h>
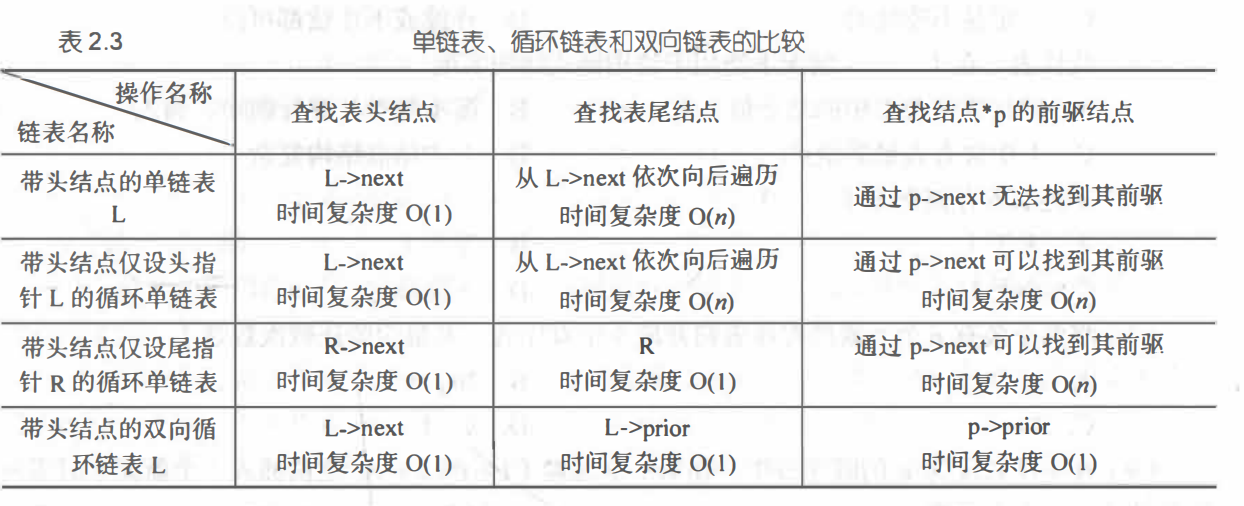
2.2.3 循环链表

| 链表类型 | 当前指针p是否指向表尾结点的终止条件 |
| 单链表 | p!=NULL或p->next!=NULL |
| 循环链表 | p!=L或p->next!=L |
2.2.4 双向链表
双向链表:相比单链表,其有两个指针域,一个指向直接前驱,一个指向直接后继。
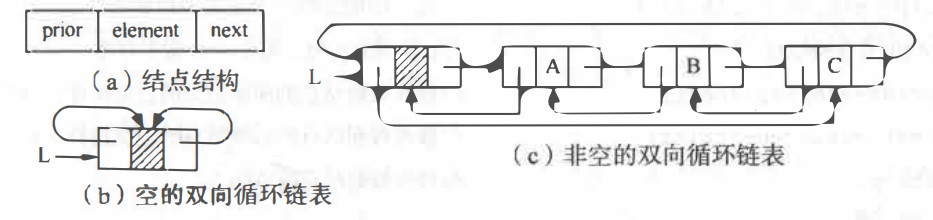
2.2.4.1 双向链表的定义和表示
typedef int ElemType;
typedef struct DuLNode
{
struct DuLNode *prior;//用于指向直接前驱的指针域
ElemType data;//数据域
struct DuLNode *next;//用于指向直接后继的指针域
}DuLNode,*DuLinkList;
2.2.4.2 双向链表的基本操作与实现
2.2.4.2.1 双向链表的初始化
//双向链表的初始化
int InitList_DuL(DuLinkList *L)
{
(*L)=(DuLinkList)malloc(sizeof(DuLNode));//以头指针(*L)作为分配空间的基地址
(*L)->next=NULL;//头结点的后继指针域设为空
(*L)->prior=NULL;//头结点的前驱指针设为空
printf("空的双向链表创建成功!!!");
return 0;
}
Tip:①双向链表的初始化和单链表基本一致,这里将头结点的前驱指针域赋值为空,方便后面测试前驱指针域是否两两相连
2.2.4.2.2 头插法创建双向链表
这里就先讲一下双向链表的插入,单链表只需改动后继指针域next,而双向链表还要改动前驱指针域prior。
值得注意的是是否在尾结点后面插入。其操作也有所不同。
尾部插入:
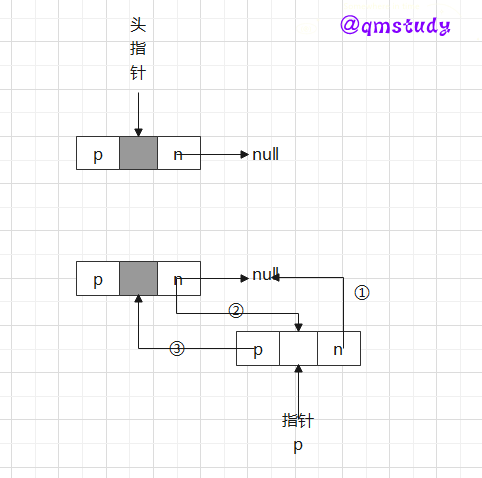
非尾部插入:
//头插法创建双链表
int CreateListHead_DuL(DuLinkList *L,int n)
{
DuLinkList p;//指向新结点的指针
int i;
srand((int)time(0));//使每次运行程序产生的随机数不同
for(i=0;i<n;i++)
{
p=(DuLinkList)malloc(sizeof(DuLNode));
p->data=rand()%100+1;
if((*L)->next!=NULL)//如果,存在首元结点
{
(*L)->next->prior=p;//首元结点的前驱指针域指向新结点*p
}
p->next=(*L)->next;//结点*p的后继指向首元结点,第一次为空。
(*L)->next=p;//头结点的后继指针域指向新结点*p
p->prior=(*L);//新结点的前驱指针域指向头结点
printf("testing:头插法第%d次插入数据%d\n", i + 1, p->data);
}
printf("链表(头插法)插入结点成功\n");
return 0;
}
Tip:①考虑到尾部插入和非尾部插入操作有些不同,算法中进行了插入位置是否为尾部的判断。
②当然这里是头插法,只需判断是否存在首元结点即可(在头结点后插入结点)。
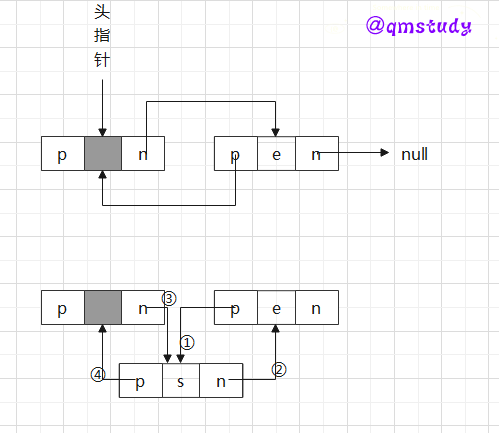
2.2.4.2.3 双向链表的插入
以上已经讲述插入的方法,知晓其与单链表插入的异同,还需要注意尾部和非尾部插入的情况。
//双向链表的插入(插入到末尾时有所不同)
int ListInsert_DuL(DuLinkList *L,int i,ElemType e)
{
DuLinkList p;
p=(*L);//指针p指向头结点
int j=0;
while(p&&j<i-1)//循环结束如果i位置合法,p指向第(i-1)个结点
{
j++;
p=p->next;
}
if(!p||j>i-1)
{
printf("\n插入位置位置i=%d非法!!!",i);
return -1;
}
DuLinkList s=(DuLinkList)malloc(sizeof(DuLNode));//定义个新结点*s
s->data=e;
s->next=p->next;//新结点*s的后继指针域指向第i个结点(第i-1个结点为尾结点时指向空),
if(p->next)//如果第(i-1)个结点不是尾结点(在两个结点中插入)。
{
p->next->prior=s;//第i个结点的前驱指针域指向新结点*s
}
s->prior=p;//新结点*s的前驱指针域指向第i-1个结点
p->next=s;//第i-1个结点的后继指针域指向新结点*s
printf("\n在位置:%d插入元素:%d成功",i,e);
return 0;
}
Tip:①考虑到尾部插入和非尾部插入操作有些不同,算法中进行了插入位置是否为尾部的判断。
2.2.4.2.4 双向链表的删除
双向链表的删除操作和单链表不同,和插入类似,尾部结点和非尾部结点的删除情况也不同。
尾部结点删除:
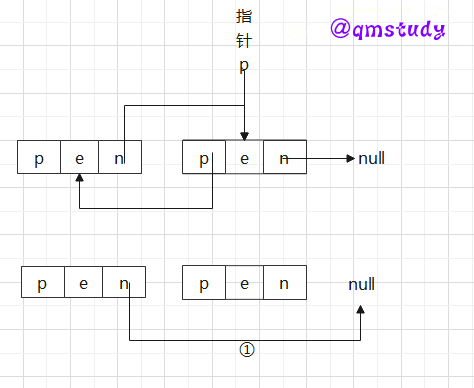
非尾部结点删除:
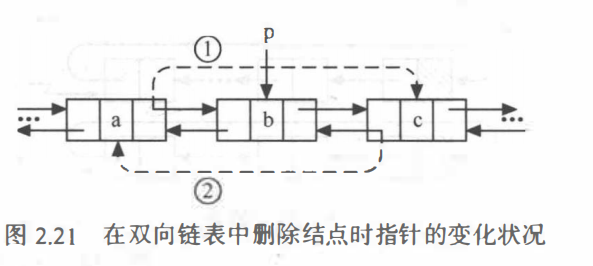
//双向链表的删除(删除尾结点有所不同)
int ListDelete_DuL(DuLinkList *L,int i)
{
DuLinkList p,q;
p=(*L);//p指向头结点
if(!p->next)
{
printf("\n该表为空!!!");
}
int j=0;
while(p->next&&j<i)//循环结束指针p指向第i个结点
{
j++;
p=p->next;
}
if(!p||j>i)
{
printf("\n要删除的位置i非法!!!");
return -1;
}
q=p;//存放要删除的结点的地址
p->prior->next=p->next;//-------------------------------------------------①
if(p->next)//如果i位置的结点不是尾结点,后继结点不为空。
{
p->next->prior=p->prior;//--------------------------------------------②
}
free(q);//删除结点后释放其空间
printf("\n删除位置为%d的结点成功",i);
return 0;
}
Tip:①注意区分删除尾结点和非尾结点的情况。
1.为什么单链表的插入和删除没有这种差别呢?
小明:这种差别其实是对双链表的前驱指针域操作造成的
①插入:插入一个新结点,假如是在两结点直接插入,所插入结点的直接后继结点的前驱指针域需指向所插入结点。假如是在尾部插入,所插入结点无后继(后继指针域指向为空),则不存在对后面结点的前驱指针域的操作,因为所插入结点的直接后继结点不存在。
②删除:删除一个结点,假如删除非尾部结点,所删除的结点有直接后继结点,直接后继结点的前驱指针域需指向所删除结点的直接前驱结点,假如是删除尾部结点,则所删除无直接后继结点。无对直接后继结点的前驱指针域的操作。
2.那为什么第一个结点和非第一个没有这种差别呢?
小明:小编文章讲的表都是带头结点的,第一个结点一定有一个直接前驱那就是头结点。
2.2.4.2.5 双向链表的打印
//双向链表的打印
int PrintfDuList(DuLinkList *L)
{
printf("\n----------打印整个链表----------\n");
int i=0;
DuLinkList p;
p=(*L)->next;
if(p==NULL)
{
printf("\n这是一个空表!!!");
return -1;
}
while(p)
{
i++;
printf("%d(%d)->",p->data,i);
p=p->next;
}
return 0;
}
2.2.4.2.6 双向链表前驱指针域连接的判断
原理步骤:
①先找到尾结点。
②从尾结点开始顺着前驱指针域依次将每个结点的数据域的值输出。
//测试前驱指针域是否两两相连,从尾结点顺着前驱指针域依次打印各结点的数据域的值即可
int PriorTest(DuLinkList *L)
{
DuLinkList p;
p=(*L);
int i=0;
if(!p->next)
{
printf("\n这是一个空表!!!");
return -1;
}
while(p->next)//while循环结束p指向尾结点
{
i++;
p=p->next;
}
printf("\n从尾结点顺着前驱指针域依次打印各结点的数据域的值");
while(p)
{
printf("%d(%d) ",p->data,i);
i--;
p=p->prior;
}
return 0;
}
2.2.4.2.7 主函数的实现
int main()
{
DuLinkList *L;//指向头指针的二级指针L
DuLinkList DuListHead;//头指针DuList
L=&DuListHead;//L指向头指针DuList
InitList_DuL(L);//初始化双向链表
printf("\n请输入链表插入(头插法)元素个数:");
int n;
scanf("%d",&n);
CreateListHead_DuL(L,n);//头插法创建双向链表
PrintfDuList(L);//打印双向链表
printf("\n请输入要插入的位置:");
int i;
scanf("%d",&i);
printf("\n请输入要插入到%d位置的结点的数据域的值:",i);
ElemType e;
scanf("%d",&e);
ListInsert_DuL(L,i,e);//在i位置插入数据域值为e的结点
PrintfDuList(L);//打印双向链表
printf("\n请输入要删除结点的位置:");
scanf("%d",&i);
ListDelete_DuL(L,i);//删除i位置的结点
PrintfDuList(L);//打印双向链表
PriorTest(L);//前驱指针域测试
return 0;
}
2.2.4.2.8 结果演示
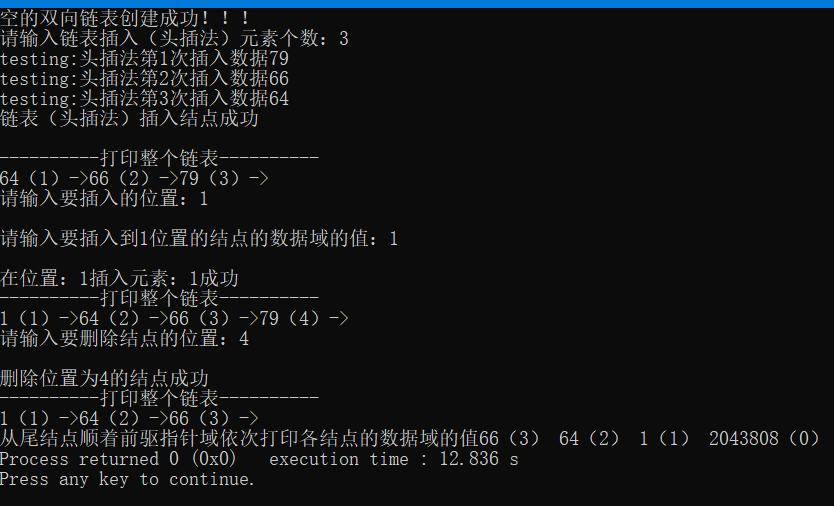
注意:代码连起来,即可运行(当然开头导入两个头文件)。
#include<stdio.h>
#include<stdlib.h>
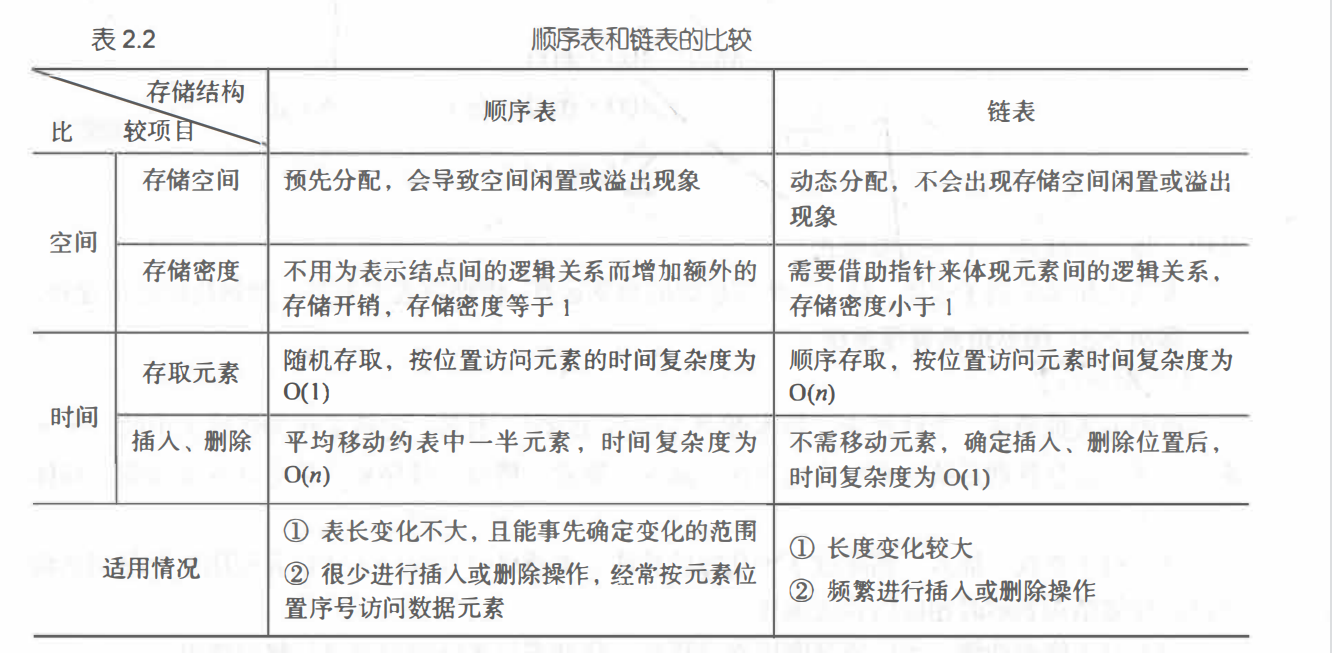
2.3 顺序表和链表的比较
2.3.1 空间性能的比较
2.3.2 时间性能的比较
*2.4 线性表的应用
2.4.1 线性表的合并
求解一般集合的并集
已知集合A={0,6,1,2},集合B={0,7,2,1},求集合A,B的并集,易得他们的并集{0,6,1,2,7},下面通过运用线性表来进行操作。
算法步骤:
①我们可以创建两个顺序表LA,LB,
②把集合A的成员插入表LA中,集合B的成员插入表LB中。
③从表LB第一个元素开始,每次与表LA所有元素进行比较。
④如果无相同的元素,则将其元素值赋值到LA中,否则不操作----这里可用查找函(LocateElem)数进行判断。
void BinJi(List *LA,List *LB)
{//将所有在线性表 LB中但不在LA中的数据元素插入到LA中
int m=ListLength(LA); //求线性表的长度
int n=ListLength(LB); //求线性表的长度
ElemType e,*pe;
pe=&e;
for(i=l;i<=n;i++)
{
GetElem(LB,i,pe); //取 LB中第l.个数据元素赋给 e
if (! LocateElem (LA, e)) //LA中不存在和 e 相同的数据元素
Listinsert(LA,++m,e);//将 e 插在LA的最后
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号