算法 - 牛顿迭代法求平方根

[LeetCode(Q69)] Sqrt(x) (编程实现sqrt)

 

Q: 

Implement int sqrt(int x).

Compute and return the square root of x.

A:

这里给出两种实现方法：一是二分搜索，二是牛顿迭代法。

1. 二分搜索

对于一个非负数n，它的平方根不会小于大于（n/2+1）（谢谢@linzhi-cs提醒）。在[0, n/2+1]这个范围内可以进行二分搜索，求出n的平方根。

 1 int sqrt(int x) {
 2     long long i = 0;
 3     long long j = x / 2 + 1;
 4     while (i <= j)
 5     {
 6         long long mid = (i + j) / 2;
 7         long long sq = mid * mid;
 8         if (sq == x) return mid;
 9         else if (sq < x) i = mid + 1;
10         else j = mid - 1;
11     }
12     return j;
13 }

注：在中间过程计算平方的时候可能出现溢出，所以用long long。

2. 牛顿迭代法

   为了方便理解，就先以本题为例：

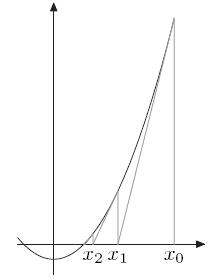
   计算x² = n的解，令f(x)=x²-n，相当于求解f(x)=0的解，如左图所示。

   首先取x₀，如果x₀不是解，做一个经过(x₀,f(x₀))这个点的切线，与x轴的交点为x₁。

   同样的道理，如果x₁不是解，做一个经过(x₁,f(x₁))这个点的切线，与x轴的交点为x₂。

   以此类推。

   以这样的方式得到的x_i会无限趋近于f(x)=0的解。

   判断x_i是否是f(x)=0的解有两种方法：

   一是直接计算f(x_i)的值判断是否为0，二是判断前后两个解x_i和x_i-1是否无限接近。

 

经过(x_i, f(x_i))这个点的切线方程为f(x) = f(x_i) + f’(x_i)(x - x_i)，其中f'(x)为f(x)的导数，本题中为2x。令切线方程等于0，即可求出x_i+1=x_i - f(x_i) / f'(x_i)。

继续化简，x_i+1=x_i - (x_i² - n) / (2x_i) = x_i - x_i / 2 + n / (2x_i) = x_i / 2 + n / 2x_i = (x_i + n/x_i) / 2。

有了迭代公式，程序就好写了。关于牛顿迭代法，可以参考wikipedia以及百度百科。

 1 int sqrt(int x) {
 2     if (x == 0) return 0;
 3     double last = 0;
 4     double res = 1;
 5     while (res != last)
 6     {
 7         last = res;
 8         res = (res + x / res) / 2;
 9     }
10     return int(res);
11 }

牛顿迭代法也同样可以用于求解多次方程的解。

P.S. 本题是求解整数的平方根，并且返回值也是整型。在上述代码基础上稍微做修改，就可以同样适用于double（仅限方法2）。

 1 double sqrt(double x) {
 2     if (x == 0) return 0;
 3     double last = 0.0;
 4     double res = 1.0;
 5     while (res != last)
 6     {
 7         last = res;
 8         res = (res + x / res) / 2;
 9     }
10     return res;
11 }