诊断偏差（bias）和方差（variance）

以下两个图是比较熟悉的高偏差（high bias）与高方差（high variance）的图

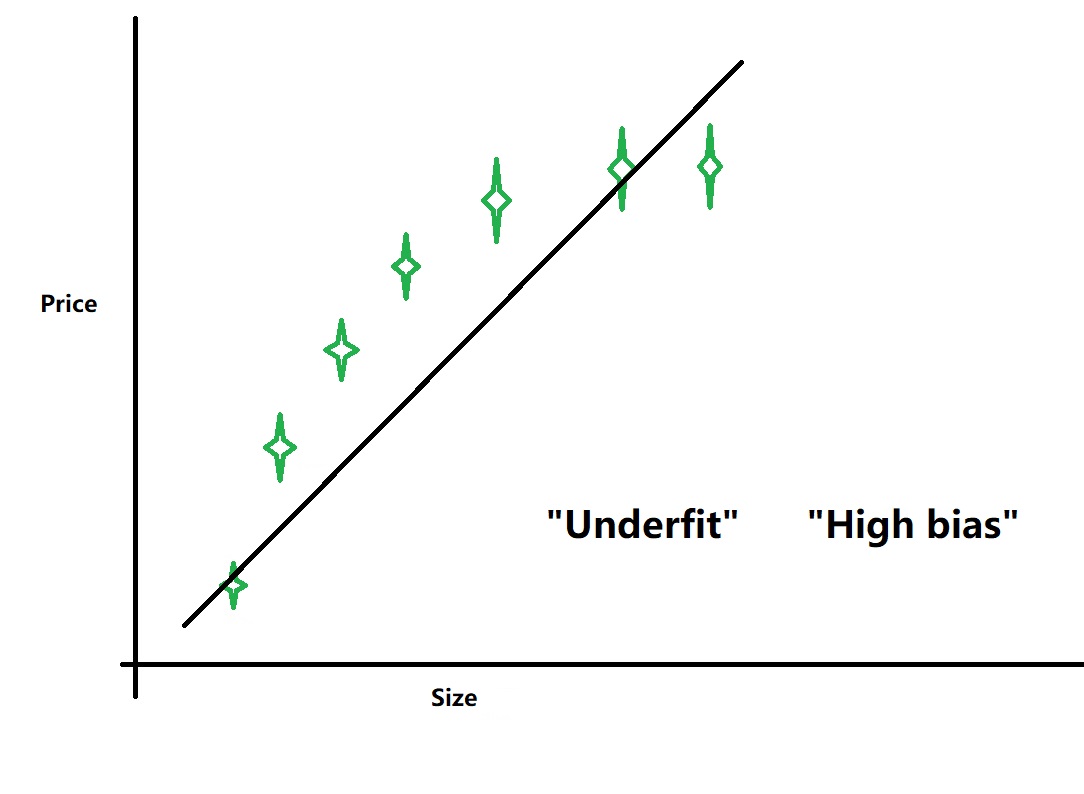
\[{h_\theta }\left( x \right) = {\theta _0} + {\theta _1}x\]

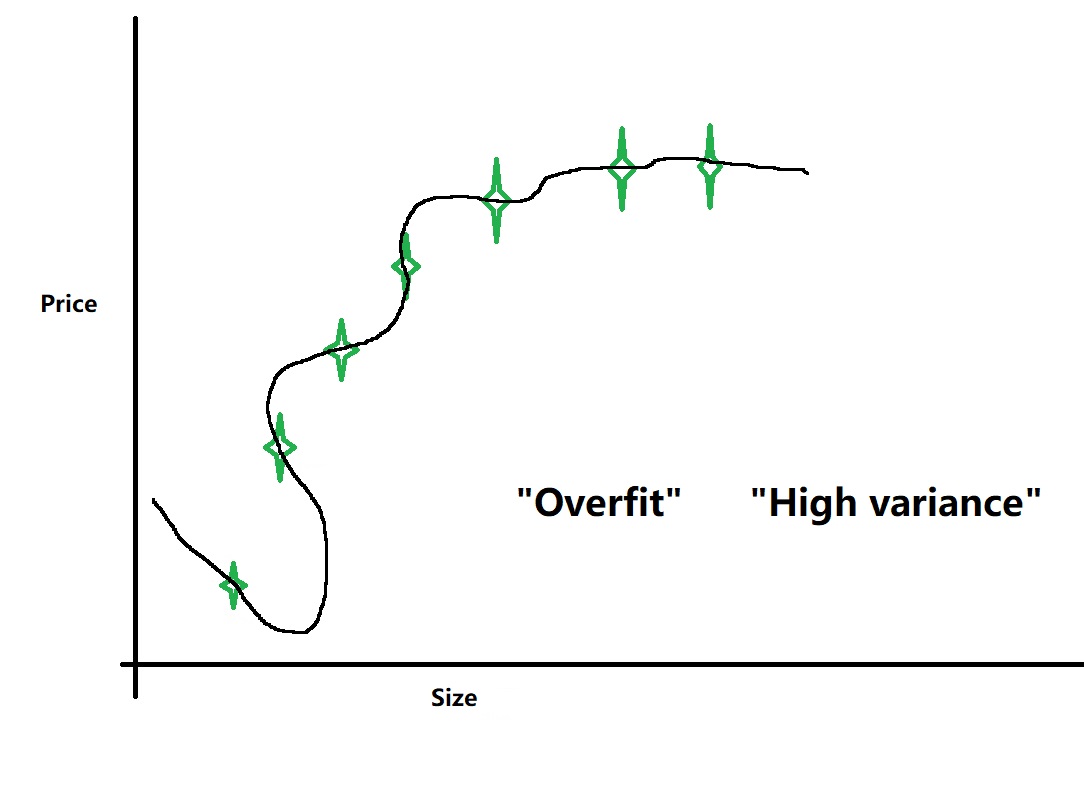
\[{h_\theta }\left( x \right) = {\theta _0} + {\theta _1}x + {\theta _2}{x^2} + {\theta _3}{x^3} + {\theta _4}{x^4}\]

接下来画“误差”（error）图

训练误差：

\[{J_{train}}\left( \theta  \right) = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right)}^2}} \]

交叉验证误差：

\[{J_{CV}}\left( \theta  \right) = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {x_{CV}^{\left( i \right)}} \right) - y_{CV}^{\left( i \right)}} \right)}^2}} \]

---

 

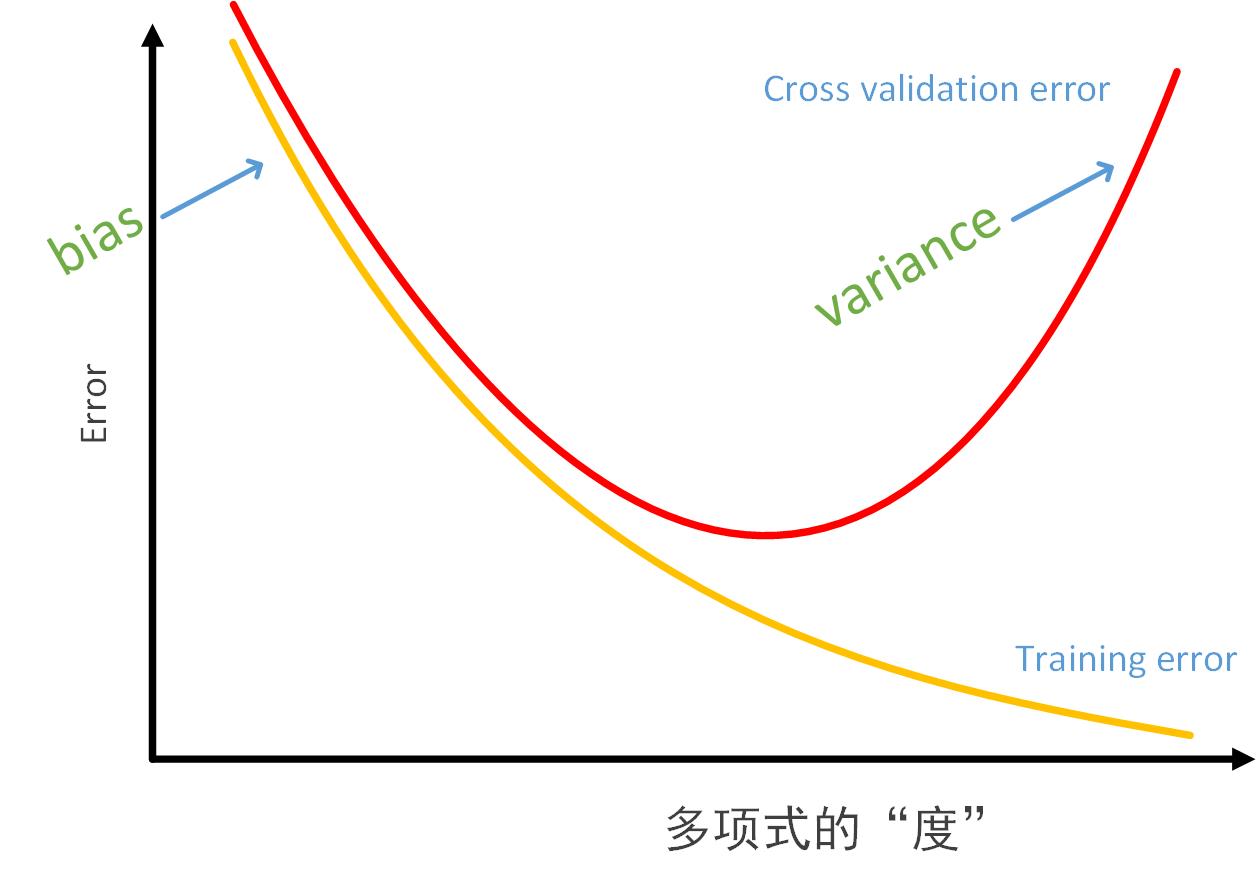
多项式的度（补充概念）

定义如下

\[\begin{array}{l}
{h_\theta }\left( x \right) = {\theta _0} + {\theta _1}x\\
{h_\theta }\left( x \right) = {\theta _0} + {\theta _1}x + {\theta _2}{x^2}\\
.\\
.\\
.\\
{h_\theta }\left( x \right) = {\theta _0} + {\theta _1}x + ... + {\theta _{10}}{x^{10}}
\end{array}\]

多项式的度从d=1到d=10（主要是方便理解，意在表达多项式越来越复杂，越来越适应训练数据）

---

 

从图中可以看出（也比较容易理解）随着多项式度的增加，训练误差在逐渐变小，因为“假设函数（多项式）”正在越来越适应训练集；而交叉验证误差先减小然后增大。因为刚开始“假设函数”处于“underfit”的情况，这时模型对训练集和交叉验证集的适应性都不好。随着度的增大，模型越来越接近“just right”状态，这时，交叉验证误差达到最小值。当度再继续增大时，模型就会对训练数据产生“voerfit”现象，这样交叉验证集的误差就会升高。

 总结

• 在“高偏差”（high bias）情况下，“训练误差”和“交叉验证误差”都很大
• 在“高方差”（high variance）情况下，“训练误差”较小，“交叉验证误差”较大（或者“交叉验证误差”比“训练误差”大得多（>>））