2025.10.10 测试

Bully Sort

or2 初绘场切 *3500 。

发现这个过程很像冒泡排序，思考每进行一次操作让什么势函数减少了恰好 \(1\) 。

这样我们就可以将操作次数转换为求势函数。

对于一次交换， \(x\) 与 \(y\) ，序列尾端有若干个元素在正确的位置，形如：

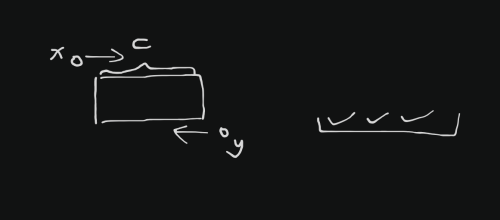
因为 \(x\) 是位置不正确中最大的，而 \(y\) 是其右侧最小的，所以 \(y\) 应该在的位置一定不在 \(x\) 右侧。

所以，假如其中间有 \(c\) 个其他的数，那么这 \(c\) 个数值域一定在 \((y, x)\) 内。

所以 \(x\), \(y\) 都距离自己的终点进了 \((c+1)\) ，而整个序列的逆序对减少了 \(2c + 1\) 。

所以 接近的距离 - 逆序对变化量 = 1

所以设 \(\Phi = \sum \left|i-p_i\right| - f\) ， \(f\) 为序列的逆序对个数。

可以发现，每次操作会让 \(\Phi\) \(-1\) ，而最终 \(\Phi=0\) 。

动态逆序对可以使用各种方法，前者是可以 \(O(1)\) 维护的。

Bridge Club

相互可以配对的元素下表的 \(popcount\) 奇偶性一定不同，将为奇的作为左部点，为偶的作为右部点。

费用流处理最大权二分图匹配。

但这样的点数边数太多了。

发现每选择一对点，都会导致有大概 \(2n\) 条边不能匹配，所以有效边只有权值前 \(2nk\) 大的边。

保留下来这部分费用流就对了。

Code

Good Subsegments

充要条件为 \(max-min=r-l\) 。

扫描线固定 \(r\) ，则判定有多少个 \(l\) 满足 \(max-min+l=r\) 。

因为 \(max-min\ge r-l\) ，所以 \(max-min+l\ge r\) 。

只需要判断左侧的最小值即可。

使用吉司机线段树维护最小值个数，支持区间加以及区间最小值 \(ans+1\) 。

Code