时空复杂度再入门

规定

渐近记号

我们往往希望通过某些东西来度量我们消耗资源的多少，在算法竞赛中，一般为空间和时间。
我们希望知道对于某个 \(\boldsymbol{问题}\) ，我们的算法所消耗的资源随着 \(\boldsymbol{实例}\) 规模的变化将如何变化。

我们认为，我们的算法是可界定的，即运行时间是可以通过输入规模（比如说数组长度 \(n\)）的一个函数 \(f(n)\) 来大概描述的。

举个插入排序的例子，对于一个大小为 \(n\) 的实例，\(f(n)=an^2+bn+c\) ，其中 \(a,b,c\) 是非负常实数。
在 \(n\) 足够大时，低次项以及高次项常数带来的影响往往可以忽略。
所以我们可以称插入排序的复杂度为 \(\Theta(n^2)\) 。

发现我们其实是在描述运行时间随着输入规模增长而增长的速度。

下面我们给出三种渐进符号的形式化定义。

渐近紧确界 \(\Theta\)

记 \(g(n)\in \Theta(f(n))\) ，当且仅当 \(\exist\) 非负常数 \(c_1, c_2:\) \(\exist\) \(n_0>0\) ，\(\forall\) \(n>n_0\) , \(0< c_1f(n)\le g(n)\le c_2f(n)\) 。

渐近上界 \(\Omicron\)

记 \(g(n)\in \Omicron(f(n))\) ，当且仅当 \(\exist\) 非负常数 \(c:\) \(\exist\) \(n_0>0\) ，\(\forall\) \(n>n_0\) , \(0<g(n)\le cf(n)\) 。

渐进下界 \(\Omega\)

记 \(g(n)\in \Omega(f(n))\) ，当且仅当 \(\exist\) 非负常数 \(c:\) \(\exist\) \(n_0>0\) ，\(\forall\) \(n>n_0\) , \(0< cf(n)\le g(n)\) 。

放一张图来辅助理解。

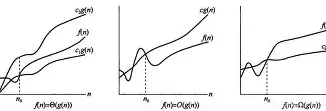
但是形式化的定义太过繁琐，我们一般非形式化地直接称某部分消耗资源是 \(\Theta(f(n))\) 的。
所以 \(\Theta (n^2)\) 就意味着运行时间随着输入规模增加呈平方量级的增长。

我们一般只关心其效率，更具体的，关心其最差情况下的运行时间。
所以上界 \(O\) 记号是最常用的。
同时，有时影响效率的不可忽略的不只一个变量，同时可能并非是关于变量的一个多项式函数。
所以我们可以见到诸如 \(O(q\sqrt n)\) ， \(O(n\log^2 n)\) , \(O(n^33^n)\) 的式子。
当运行时间与输入规模无关时，复杂度是 \(\Theta(1)\) 的。

小结，你需要知道 \(O(f({n}))\) 是某项资源的增长量级上界即可。
（我当年怎么没人给我讲严谨的内容）
（不过讲了也没什么用就是了）

时间复杂度分析的常用方法

数循环层数

for (int i = 1; i <= n; ++i)
	for (int j = 1; j < n; ++j)
		if (a[j] > a[j + 1]) std::swap(a[j], a[j + 1]);

复杂度 \(O(n^2)\) 。

调和级数

for (int i = 1; i <= n; ++i)
	for (int j = 1; j <= n; j += i)
		//solve…

复杂度相当于 \(n + \frac{n}{2} + \frac{n}{3} + \cdots + 1 \approx n\ln n = O(n\log n)\) 。

主定理

以归并排序为例，每次将当前问题分治为两个规模更小的子问题，然后用 \(\Theta(n)\) 的复杂度合并。
可以写出递推式，设 \(T(n)\) 为将长度为 \(n\) 的序列排好序所需的时间。

\[T(n)=\left\{\begin{matrix}\Theta(1) & n=1\\ 2T(\frac{n}{2})+\Theta(n) & n > 1 \end{matrix}\right. \]

Link

复杂度为 \(O(n\log n)\) 。

摊还分析（势能分析法）

以下文字摘自 oi-wiki:

势能分析（Potential Method）通过定义一个势能函数（通常表示为 \(\Phi\)），度量数据结构的 潜在能量，即系统状态中的预留资源，这些资源可以用来支付未来的高成本操作。势能的变化用于平衡操作序列的总成本，从而确保整个算法的均摊成本在合理范围内。

以 set 维护区间推平为例。
我们需要维护的操作如下：

• 修改端点处的两个颜色段
• 删除之间的所有颜色段
• 插入一个新的颜色段

我们认为 \(n, q\) 同阶，则复杂度为 \(O(n\log n)\) 。
需要严谨证明的是第二个删除操作，单次删除最多可达 \(O(n)\) ，但这样的复杂度为什么不是 \(O(n^2)\) 呢？
我们定义势函数 \(\Phi\) 为 \(set\) 的元素个数，即颜色段个数。
每次修改操作最多会使 \(\Phi\) 增加 \(\Theta(1)\) ，而 \(\Phi\) 初始值为 \(O(n)\) 。
每次删除操作会使 \(\Phi\) 减少 \(1\) ，因为 \(\Phi\) 始终非负，所以删除操作最多进行 \(O(n)\) 次。
所以复杂度为 \(O(n\log n)\) 。

空间复杂度的相关知识

数据单位

bit 位：最小单元，只有 \(0,1\) 两种状态。
byte 字节： \(8\) bit
KB 千字节： \(2^{10}\) byte
MB 兆字节: \(2^{10}\) KB
GB 吉字节: \(2^{10}\) MB

一个 int 一般占四个字节， long long 占八个字节。
其他类型请 BFS(bing first search) 。

堆栈空间

栈空间：函数调用即局部变量所使用的空间。
堆空间：静态变量以及动态分配内存所用的空间。

int a;//堆空间
int main() {
	int b;//栈空间
}

栈空间由系统自动分配，堆空间一般通过 new delete 关键字手动管理（一般不用）。

栈空间一般并不大，当申请内存大于剩余内存时会 RE ，即 \(\boldsymbol{爆栈}\) 。
老师可能会让你将数组定义在 main 函数外，这样能定义更多，就是这个原理。
题目的栈空间大小一般与空间限制相同，但本地是系统自动分配的，可能提交可过但本地 RE 。

下面提供本地手动加大栈空间的编译命令。
-Wl,--stack=1280000000

技巧

算好时空复杂度。
提供一份更好的代码模板来尽可能减少因为失误导致的 TLE MLE 。

#include <bits/stdc++.h>

using namespace std;

bool FIRPOS;

//定义所需变量及数组

bool ENDPOS;

int main() {
	int c1 = clock();
	//solve…
	
#ifdef DEBUG
	cerr << clock() - c1 << " ms " << fabs(&ENDPOS - &FIRPOS) / 1024 / 1024 << " MB\n";
	return 0;
#endif
}

编译命令加上 -DDEBUG 。

无法测试由 vector queue 等带来的内存占用，但是可以测试其初始化指针的大小。

其他技巧

• 1000 ms 内大概能处理 \(5\times 10^8\) 次运算，可以将 \(n\) 的上界代入复杂度大概估算。

如 \(O(n\log^2 n)\) 大概可以接受 \(n=10^6\) 的输入。
还有很多细节，如 常数，是否跑的满 等等。
在后续的学习中自己感觉吧。