DpsD everyday

2025-9-3

Coloring Brackets

第一天选水了。
设 \(f[l,r,a,b]\) 表示合法匹配区间 \([l,r]\) 内的染色方案，要求左端点是 \((\) 且染色状态为 \(a\) ，右端点是 \()\) 且染色状态为 \(b\) 。
直接分讨转移即可。

Record

Sonya and Bitwise OR

对于单次询问，考虑 \(cdq\) 分治。
然后发现，按位或是满足单调性的运算，可以使用双指针统计，进一步发现，\(\boldsymbol{或运算的值最多改变\log 次}\) 。
所以可以提前预处理中点向两边或的值改变的位置，这样可以 \(\log n\) 合并。
把这个过程放到线段树上，就可以解决本题。复杂度 \(O(n\log n\log a)\) 。

Record

2025-9-4

宝藏

经典的放缩限制。
记 \(f[i, S]\) 为目前树的集合为 \(S\) ，最大深度为 \(i\) （根深度为 \(0\))
枚举子集 \(T\) 表示第 \(i\) 层的节点，预处理出 \(T\) 与 \(S/T\) 的最短距离和，直接转移。
最优方案一定会被统计到，且不合法的方案代价一定会被多算，所以没影响。
复杂度 \(O(n3^n)\) 。
（这里少预处理一些东西，做到 \(O(n^23^n)\) ）。

Record

列队

发现修改只会涉及到当前行以及最后一列，将最后一列单独维护，剩下的按行维护。
各开一棵平衡树，树上节点维护二元组 \((l, len)\) 表示以 \(l\) 开头的一段长为 \(len\) 的区间。
文艺平衡树直接维护即可。

Record

2025-9-5

好困啊，做点水题。

构造数组

%%% @shanganze dalao
记 \(m=\sum b\) ，原题转化为有 \(\frac{m}{2}\) 个本质不同盒子，\(n\) 种数，问每个盒子装两个数，要求不同种的方案数。
记 \(f[i, k]\) 表示考虑完前 \(i\) 种数，目前有 \(k\) 个盒子已经装满。
这样存状态我们便可以 \(O(1)\) 得知有 \(x\) 个盒子只装了 \(1\) 个，\(y\) 个盒子是空的。
然后枚举下一种数用了 \(c\) 个只装了一个的盒子，剩下 \(b-c\) 装到了空盒子里，因为要求盒子里的两个数是不同种的。
再乘上一些二项式的转移系数就做完了，复杂度小常数 \(O(m^2)\) 。

Record

作业

第一问主席树，第二问莫队套树状数组即可。
Record

2025-9-6

小星星

图上 DP 首先排除，我们在树上 \(DP\) 。
记 \(f[u, x, S]\) 为 \(u\) 子树内节点映射到图上的集合为 \(S\) ，且 \(u\) 映射到 \(x\) 的方案数。
转移时枚举子集并判断合法性，复杂度 \(O(n^33^n)\) 。
考虑优化，枚举子集肯定是要丢掉的。
想想我们为什么需要记录这一维状态，因为题目要求映射是个双射，所以需要记录哪些还可以被映射。
我们记 \(g(S)\) 为映射到的集合为 \(S\) 的方案数，答案即为 \(g(U)\) ，因为一个点只会映射一个点。
但这样 \(DP\) 似乎更不可做了，我们再次放松限制。
记 \(h(S)\) 为映射到的元素必须属于集合 \(S\) 的方案数。
则根据子集反演相关知识，有

\[h(S)=\sum_{T\subseteq S}g(T)\Leftrightarrow g(S)=\sum_{T\subseteq S}(-1)^{\left|S\right|-\left|T\right|} h(T) \]

然后我们就可以只算 \(h(S)\) 了。
枚举 \(S\) ，规定只有 \(S\) 内的元素是可用的，记 \(f[u, x, S]\) 为 \(u\) 映射 \(x\) , \(u\) 子树内映射全部属于 \(S\) 的方案数。
转移：

\[f[u, x, S]=\prod_v \sum_{e(x, y)\in E} f[v, y, S]\\ h[S]=\sum_x f[rt, x, S] \]

Record

冰火战士

记 \(f(d)\) 为场地温度为 \(d\) 时冰战士的总能量， \(g(d)\) 火战士同理。
题目即要求

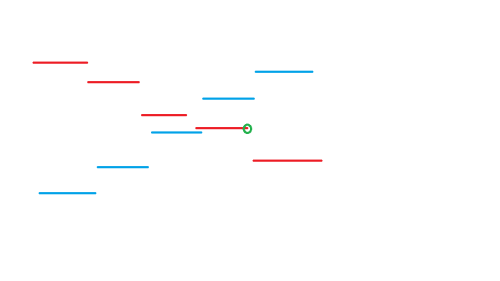
图中的交点，离散且有平台，排除三分。
我们可以二分找到 \(f(d)\le g(d)\) 的最大的 \(d\) ，以及 \(g(d + 1)=g(d')\) 的最大的 \(d'\) 。
（可以画图，容易发现这两种情况）
两者取较优即可。

但是二分套 \(BIT\) \(\log^2 n\) 的复杂度难以接受，参考线段树上二分，我们发现 \(BIT\) 同样具有优秀的结构。
具体的，我们在 \(BIT\) 上倍增，从高到低逐个确定 \(d\) 的每一位。
假设 \(BIT\) 的数组为 \(c\) ，枚举在考虑第 \(k\) 位，已累加的贡献为 \(nw\) 。
则如果 \(nw + c[d+2^k]\) 合法，则 \(d\leftarrow d+2^k, nw\leftarrow nw+c[d]\) 。
考虑正确性，根据 \(BIT\) 的定义， \(c[x]\) 存储着 \([x-lowbit(x)+1,x]\) 的信息，又因为我们从高到低确认。
所以 \(c[d+2^k]\) 就存储着 \([d+1, d+2^k]\) 的信息。

Record

2025-9-7

彩灯晚会

将 \(cnt_i^2\) 拆成将长度为 \(l\) 的链两两配对的方案数。
对于两条链，如果其重合了 \(x\) 个点，则有 \(k^{n-2l+x+1}\) 的系数。
但是恰好重合 \(x\) 个点（记作 \(g(x)\)）比较难做，使用二项式反演改成钦定 \(x\) 个点重合（记作 \(f(x)\)）。

则我们只需要预处理 \(dis[k, u, v]\) , \(pre[k, u]\) 和 \(suf[k, u]\) ，分别表示从 \(u\) 到 \(v\) 包含 \(k\) 个点（不含 \(u\)，含 \(v\)）的路径方案，
以 \(u\) 结尾的包含 \(k\) 个点（含 \(u\)）的方案，以 \(u\) 开头的包含 \(k\) 个点（不含 \(u\)）的方案。
不钦定任何相交点的单独处理。
记 \(f[u, x, l_1, l_2]\) 为目前钦定了 \(x\) 个重合点，最后一个钦定点为 \(u\) ，且两条链分别长 \(l_1, l_2\) 的方案数。
容易按照拓扑序转移， \(f[v, x+1, l_1+\Delta l_1, l_2+\Delta l_2] \leftarrow f[u, x, l_1, l_2]\times dis[\Delta l_1, u, v]\times dis[\Delta l_2, u, v]\) 。
复杂度 \(O(n^3l+n^2l^5)\) 。
发现枚举 \(\Delta\) 的两个过程可以分布转移，复杂度 \(O(n^3l+n^2l^4)\) 。
还是过不了，我们将答案写出来。

\[\begin{align*} ans&=\sum_{x=0}^l k^{n-2l+x+1} g(x)\\ &=k^{n-2l+1}\sum_{x=0}^l \sum_{i=x}^l (-1)^{i-x}k^x{i\choose x}f(i)\\ &=k^{n-2l+1}\sum_{i=0}^l f(i)\sum_{x=0}^ik^x(-1)^{i-x}{i\choose x}\\ &=k^{n-2l+1}\sum_{i=0}^l f(i)(k-1)^i \end{align*} \]

所以可以直接省略 \(x\) 这一维，每钦定一个乘上 \(k-1\) 的系数即可。
复杂度 \(O(n^3l+n^2l^3)\) ，注意常数，不要使用记忆化搜索初始化。

Record

曼哈顿交易

注意题意。
莫队套权值线段树，人傻常数大，使用了 zkw 科技。
Record

2025-9-8

dp 暂不公开

【模板】树套树

\(BIT\) 套权值线段树写法，通过 \(BIT\) 维护前缀根来支持待修的主席树。
线段树二分时同时在 \(\log\) 个根上走即可。

Record

2025-9-21

Photo G

记 \(f_i\) 为考虑前 \(i\) 头牛，且第 \(i\) 头牛被选中的最大值。

则 \(f_i=\max_{legal(j)} f_j +1\) 直接转移，然后只需考虑哪些 \(j\) 是合法的即可。

容易发现，如果 \(lf_i\) 为 \(r < i\) 的 \(l_{\max}\) ，\(rg_i\) 为 \(i\in [l, r]\) 的 \(l_{\min}\) （可以等价为 \(r\ge i\) 的 \(l_{min}\) ，不存在的化设为 \(i\) )

则 \([lf_i, rg_i)\) 是合法的转移区间，维护一些发现都是单调递增的，直接滑动窗口维护即可。

Record

我终将成为你的倒影

取相邻的两个数 \(\max, \min\) ，合法的必要条件是 \(\left\lfloor \frac{\max}{b} \right\rfloor - \left\lfloor \frac{\max}{b} \right\rfloor \le 1\) 。

记 \(a=b-a\bmod b\) ，分两种情况讨论。

• \(\left\lfloor \frac{\max}{b} \right\rfloor - \left\lfloor \frac{\max}{b} \right\rfloor = 0\)

  要么 \(\min\) 跳到下一个块，要么 \(\max\) 也跳不到下一个块，当 \(a\le \max \bmod b\) \(\vee\) \(a>\min \bmod b\) 时会有贡献。

• \(\left\lfloor \frac{\max}{b} \right\rfloor - \left\lfloor \frac{\max}{b} \right\rfloor = 1\)

  当 \(\min\) 跳到下一个块，且 \(\max\) 跳不到下一个块有贡献。即 \(\min \bmod b < a \le \max \bmod b\) 。

直接维护可以开 \(500\) 棵主席树，但原题卡空间。

发现主席树 初始化 - 查询是 \(O(Bn\log B) - O(\log B)\) 的，极度不平衡。

所以使用根号算法，对每一个整块预处理 \(\bmod b=a\) 的答案即可。

复杂度 \(O(n\sqrt n)\) 。

Record