那快把题端上来吧(三)
CF1814F Communication Towers
\(\boldsymbol{线段树分治}\) 。
边在某种情况下可通过,可以看做在某种情况下出现,且出现时间为端点值域的交集,考虑线段树分治。
递归到叶子节点后,和 \(1\) 在同一个连通块内的全部合法,但遍历赋值太劣了,于是我们考虑打标记。
记 \(tag[x]\) 为 \(x\) 在几个叶子节点与 \(1\) 在同一个连通块。
只需要给 \(1\) 所在连通块的根标记 \(+1\) ,然后每次撤销时下传标记。
但是,标记并非一定要下传,如果有个连通块在中途接上另一个,然后撤销就会白嫖走标记。
所以我们只维护相连这段时间标记的增量下传。
具体的,如果 \(y\) 要作为 \(x\) 的根,就将 \(tag[x]\) 减去 \(tag[y]\) ,撤销时再加回来,就可以维护出他们在同一个连通块内时根的增量。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 4e5 + 7;
const int V = 2e5;
typedef long long ll;
typedef double db;
typedef std::pair<int, int> PII;
int n, m, l[_], r[_], fa[_], sz[_], tag[_], u[_], v[_], stk[_], top;
std::vector <int> op[_ << 2];
int fnd(int x) { return fa[x] == x ? x : fnd(fa[x]); }
void mrg(int x, int y) {
if ((x = fnd(x)) == (y = fnd(y))) return;
if (sz[x] > sz[y]) std::swap(x, y);
tag[x] -= tag[y], fa[x] = y, sz[y] += sz[x], stk[++top] = x;
}
void Back(int bot) { int x; while (top != bot) x = stk[top--], tag[x] += tag[fa[x]], sz[fa[x]] -= sz[x], fa[x] = x; }
#define ls p << 1
#define rs p << 1 | 1
#define md ((s + t) >> 1)
void Mdy(int l, int r, int s, int t, int v, int p) {
if (r < s or t < l or l > r) return;
if (l <= s and t <= r) return op[p].push_back(v), void();
Mdy(l, r, s, md, v, ls), Mdy(l, r, md + 1, t, v, rs);
}
void Qry(int s, int t, int p) { int bot = top;
for (int x : op[p]) mrg(u[x], v[x]);
if (s == t) ++tag[fnd(1)];
else { Qry(s, md, ls); Qry(md + 1, t, rs); }
Back(bot);
}
#undef ls
#undef rs
#undef md
int main() {
std::ios::sync_with_stdio(false);
std::cin >> n >> m;
lep(i, 1, n) std::cin >> l[i] >> r[i], fa[i] = i, sz[i] = 1;
int x, y;
lep(i, 1, m) {
std::cin >> x >> y, u[i] = x, v[i] = y;
if (l[x] > l[y]) std::swap(x, y);
Mdy(l[y], std::min(r[x], r[y]), 1, V, i, 1);
}
Qry(1, V, 1);
lep(i, 1, n) if (tag[i] > 0) std::cout << i << ' ';
std::cout << '\n';
return 0;
}
P3527 [POI 2011] MET-Meteors
\(\boldsymbol{整体二分}\) 。
对于某个国家,可以通过二分来确定其满足要求的最早时间。
但是依次二分复杂度难以接受,于是我们便将所有国家一起进行二分。
具体的,对于 Solve(ql, qr, s, t) 表示 \(ql\sim qr\) 的国家的答案在 \(s\sim t\) 内。
然后通过 \(BIT\) 维护 \(s\sim mid\) 的操作,然后对于每个国家判断是否符合要求,分开到 \(s\sim mid\) 和 \(mid+1\sim t\) 两个区间去。
注意这里每次操作不能从 \(1\) 开始,向右递归的国家需要将要求下调,类比平衡树。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 3e5 + 7;
typedef unsigned long long ll;
typedef double db;
typedef std::pair<int, int> PII;
int n, m, k, p[_], a[_], l[_], r[_], ans[_];
int ld[_], rd[_], q[_];
ll c[_], g[_]; std::vector <int> pos[_];
void add(int x, int k) { while (x <= m) c[x] += k, x += x & -x; }
ll qry(int x) { ll res = 0; while (x) res += c[x], x -= x & -x; return res; }
#define md ((s + t) >> 1)
void Solve(int ql, int qr, int s, int t) {
if (ql > qr) return;
if (s == t) { lep(i, ql, qr) ans[q[i]] = s; return; }
lep(i, s, md) {
if (l[i] <= r[i]) add(l[i], a[i]), add(r[i] + 1, -a[i]);
else add(l[i], a[i]), add(1, a[i]), add(r[i] + 1, -a[i]);
}
int pl = 0, pr = 0;
lep(i, ql, qr) {
g[q[i]] = 0;
for (int v : pos[q[i]]) g[q[i]] += qry(v);
if (g[q[i]] >= p[q[i]]) ld[++pl] = q[i];
else rd[++pr] = q[i],p[q[i]]-=g[q[i]];
}
lep(i, s, md) {
if (l[i] <= r[i]) add(l[i], -a[i]), add(r[i] + 1, a[i]);
else add(l[i], -a[i]), add(1, -a[i]), add(r[i] + 1, a[i]);
}
lep(i, 1, pl) q[ql + i - 1] = ld[i];
lep(i, 1, pr) q[ql + pl + i - 1] = rd[i];
Solve(ql, ql + pl - 1, s, md); Solve(ql + pl, qr, md + 1, t);
}
#undef md
int main() {
std::ios::sync_with_stdio(false);
std::cin >> n >> m; int x;
lep(i, 1, m) std::cin >> x, pos[x].push_back(i);
lep(i, 1, n) std::cin >> p[i], q[i] = i;
std::cin >> k;
lep(i, 1, k) std::cin >> l[i] >> r[i] >> a[i];
Solve(1, n, 1, k + 1);
lep(i, 1, n) if (ans[i] == k + 1) std::cout << "NIE\n"; else std::cout << ans[i] << '\n';
return 0;
}
SP1805 HISTOGRA - Largest Rectangle in a Histogram
\(\boldsymbol{笛卡尔树}\) 。
每个节点有一个键值二元组 \((k, w)\) , \(k\) 满足二叉搜索树的性质, \(w\) 满足小/大根堆的性质。
可以证明对于确定了一组节点,树的结构是唯一确定的,且如果将序列下标作为 \(k\) ,那么一个子树代表一个区间。
如果我们根据 (序列下标,权值) 构建笛卡尔树,那么对于一个子树,其内所有值都大于根且编号连续。
所以原问题等价于子树大小乘权值的最大值。
下面来讲如何构建笛卡尔树,用栈维护一条右链,根据 \(k\) 依次加入 \(w\)。
找到右链上深度最大的满足 \(<w\) 的节点,然后把当前节点挂在这个点上,如果这个点本来有右儿子,挂在当前节点的左儿子上。
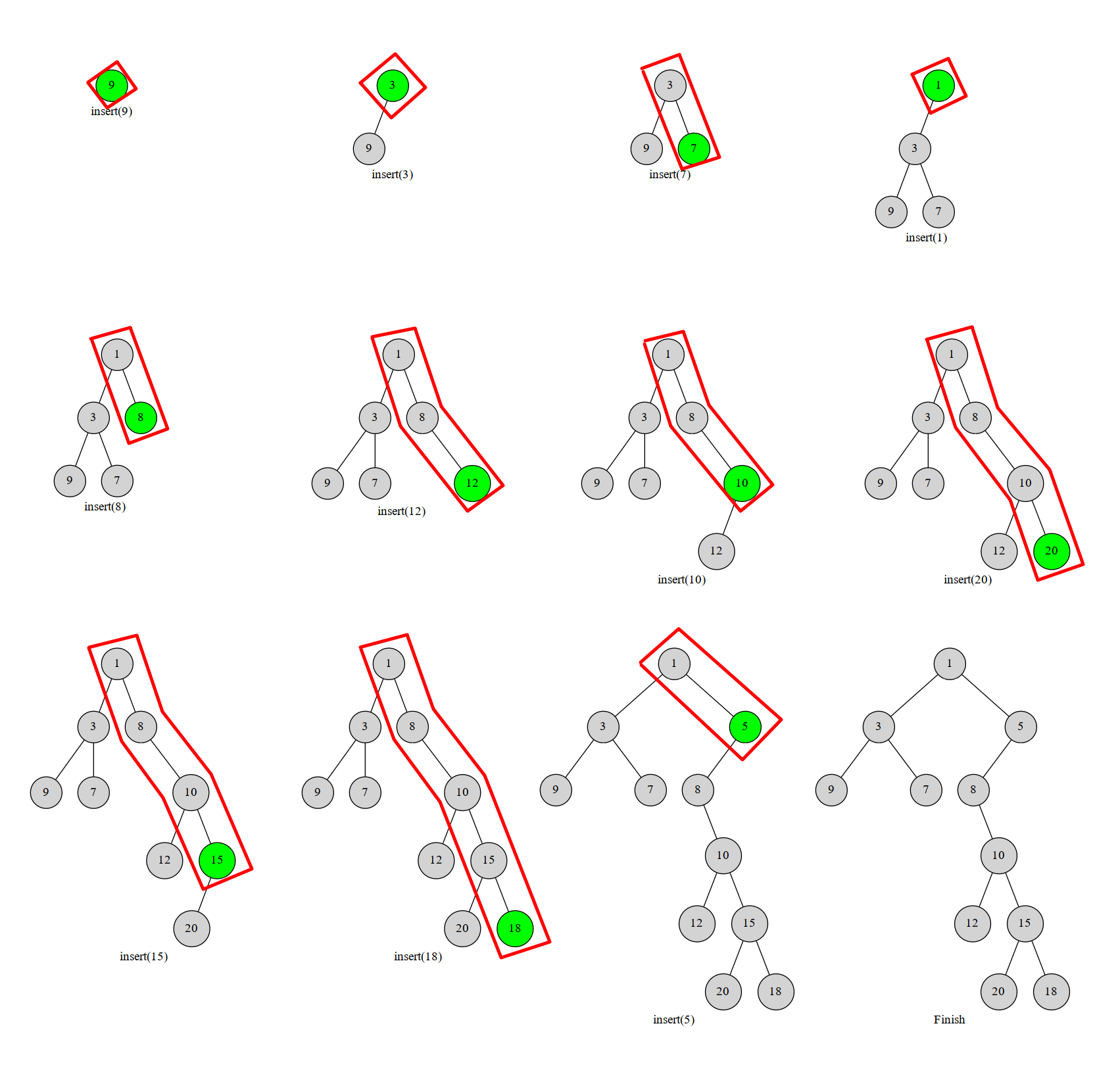
\(\boldsymbol{from}\) \(\boldsymbol{OI}\) \(\boldsymbol{Wiki}\)
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 2e5 + 7;
typedef long long ll;
typedef double db;
typedef std::pair<int, int> PII;
int n, a[_], ls[_], rs[_], stk[_], top, k, sz[_], deg[_];
ll ans;
void Dfs(int u) {
sz[u] = 1;
if (ls[u]) Dfs(ls[u]), sz[u] += sz[ls[u]];
if (rs[u]) Dfs(rs[u]), sz[u] += sz[rs[u]];
ans = std::max(ans, 1ll * sz[u] * a[u]);
}
int main() {
std::ios::sync_with_stdio(false);
while (std::cin >> n) {
if (!n) break;
lep(i, 1, n) {
std::cin >> a[i]; k = top;
while (k and a[stk[k]] > a[i]) --k;
if (k) rs[stk[k]] = i;
if (k < top) ls[i] = stk[k + 1];
stk[++k] = i, top = k;
}
lep(i, 1, n) ++deg[ls[i]], ++deg[rs[i]]; deg[0] = 0;
int rt = 1;
lep(i, 1, n) if (!deg[i]) rt = i;
Dfs(rt); std::cout << ans << '\n';
ans = top = 0;
lep(i, 1, n) deg[i] = ls[i] = rs[i] = sz[i] = 0;
}
return 0;
}
P3792 由乃与大母神原型和偶像崇拜
\(\boldsymbol{线段树, set}\)
原条件等价于这个区间是否满足无重复且 \(max-min=r-l\) 。
后者很好维护,前者可以维护每个元素上一个相同颜色的位置 \(pre\) 。
则这个条件等价于 \(\min\{pre\} < l\) ,使用 \(set\) 来辅助维护。
具体的,维护每种颜色的出现位置即可。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 5e5 + 7;
typedef long long ll;
typedef std::pair<int, int> PII;
typedef double db;
struct node { int mx, mn, pre;
friend node operator + (const node& L, const node& R) {
return { std::max(L.mx, R.mx), std::min(L.mn, R.mn), std::max(L.pre, R.pre) };
}
}tr[_ << 2];
int n, m, o[_], x[_], y[_], a[_], lst[_ << 1], pre[_];
std::set<int> S[_ << 1];
std::vector <int> Ab;
int id(int x) { return std::lower_bound(Ab.begin(), Ab.end(), x) - Ab.begin(); }
#define ls p << 1
#define rs p << 1 | 1
#define md ((s + t) >> 1)
void pu(int p) { tr[p] = tr[ls] + tr[rs]; }
void Bd(int s, int t, int p) {
if (s == t) return tr[p] = { a[s], a[s], pre[s] }, void();
Bd(s, md, ls), Bd(md + 1, t, rs); pu(p);
}
void upd(int p, node k) { tr[p] = k; }
void mdy(int d, int s, int t, node k, int p) {
if (s == t) return upd(p, k);
d <= md ? mdy(d, s, md, k, ls) : mdy(d, md + 1, t, k, rs); pu(p);
}
node qry(int l, int r, int s, int t, int p) {
if (l <= s and t <= r) return tr[p];
if (r <= md) return qry(l, r, s, md, ls); if (l > md) return qry(l, r, md + 1, t, rs);
return qry(l, r, s, md, ls) + qry(l, r, md + 1, t, rs);
}
#undef ls
#undef rs
#undef md
void ins(int c, int x) {
S[c].insert(x); auto fir = S[c].find(x), sec = fir;
mdy(x, 1, n, { c, c, fir == S[c].begin() ? 0 : *(--fir) }, 1);
if ((++sec) != S[c].end()) mdy(*sec, 1, n, { c, c, x }, 1);
}
void del(int c, int x) {
auto fir = S[c].find(x), sec = fir, pos = sec;
if ((++sec) != S[c].end()) mdy(*sec, 1, n, { c, c, fir == S[c].begin() ? 0 : *(--fir) }, 1);
S[c].erase(pos);
}
void Mdy(int x, int y) { del(a[x], x), ins(a[x] = y, x); }
bool ck(int x, int y) {
auto t = qry(x, y, 1, n, 1);
return y - x == Ab[t.mx] - Ab[t.mn] and t.pre < x;
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, n) scanf("%d", a + i), Ab.push_back(a[i]);
lep(i, 1, m) scanf("%d%d%d", o + i, x + i, y + i), Ab.push_back(y[i]);
std::sort(Ab.begin(), Ab.end()), Ab.erase(std::unique(Ab.begin(), Ab.end()), Ab.end());
lep(i, 1, n) a[i] = id(a[i]), pre[i] = lst[a[i]], lst[a[i]] = i, S[a[i]].insert(i);
lep(i, 1, m) if (o[i] == 1) y[i] = id(y[i]);
Bd(1, n, 1);
lep(i, 1, m) {
if (o[i] == 1) Mdy(x[i], y[i]);
else if (o[i] == 2) puts(ck(x[i], y[i]) ? "damushen" : "yuanxing");
}
return 0;
}
CF1515I Phoenix and Diamonds
\(\boldsymbol{倍增分块,值域分组}\) 。
(上面说的是一个东西)
将物品排序后变成这样一个问题,每个物品有体积 \(w\) ,价值 \(v\) ,数量 \(a\) 三个属性。
有一个大小为 \(c\) 的背包,从左往右依次拿,能放就放,问能获得多少价值。 支持动态修改单个 \(a\) 值。
我们将询问的 \(c\) 按照值域(或者二进制最高位分组),假设 \(c\in [2^i, 2^{i+1})\) 。
那么在一段区间内, \(c\) 最多拿走一个和自己同组的物品,以及若干个更低组的物品。
所以,我们每个线段树节点维护 \(3\log V\) 个值:
\(V_i\): 区间内 \(w<2^i\) 的物品 \(a\times v\) 之和。
\(W_i\): 区间内 \(w<2^i\) 的物品 \(a\times w\) 之和。
\(tot_i\): 想要拿走至少一个 \([2^i,2^{i+1})\) 的物品需要的最小体积。
\(V_i\), \(W_i\) 的维护是平凡的。
\(tot_i\) 的维护只需考虑那个物品是在左区间取,还是将左区间取完后在右区间取,二者取 \(\min\) 。
然后考虑询问,只需遍历线段树,设 \(c\in[2^i, 2^{i+1})\) ,有三种情况。
- \(c\ge W_{i+1}\) ,全部拿走,直接返回 \(V_{i+1}\) 。
- \(W_i\le c < tot_i\) ,同层的物品一个也拿不走,但是低层的物品可以全部拿走,直接返回 \(V_i\) 。
- 否则递归左右儿子。
考虑这样做的时间复杂度。
每出现一次 \(3\) 情况,要么是可以拿走一个同层的物品,要么是可以拿走若干个低层的物品。
无论哪一个,都会让 \(c\) 掉至少一层,\(c\) 最多只有 \(\log V\) 层。
所以复杂度为 \(O (\log n\log V)\) 。
总复杂度是 \(O ((n+m)\log n\log V)\) 。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 2e5 + 7;
const int V = 17;
typedef long long ll;
const ll inf = 1e18;
typedef double db;
typedef std::pair<int, int> PII;
int n, q, v[_], w[_], id[_], ud[_];
ll sV[_ << 2][V + 1], sW[_ << 2][V + 1], tot[_ << 2][V + 1], a[_];
#define ls p << 1
#define rs p << 1 | 1
#define md ((s + t) >> 1)
void pu(int p) {
lep(i, 0, V) sV[p][i] = sV[ls][i] + sV[rs][i], sW[p][i] = sW[ls][i] + sW[rs][i],
tot[p][i] = std::min(tot[ls][i], sW[ls][i] + tot[rs][i]);
}
int lg(ll v) { return std::min(V, (int)std::log2(v)); }
void bd(int s, int t, int p) {
if (s == t) {
#define s id[s]
lep(i, lg(w[s]) + 1, V) sV[p][i] = 1ll * v[s] * a[s], sW[p][i] = 1ll * w[s] * a[s];
lep(i, 0, V) tot[p][i] = inf;
tot[p][lg(w[s])] = w[s]; return;
#undef s
} bd(s, md, ls), bd(md + 1, t, rs); pu(p);
}
void mdy(int d, int s, int t, int k, int p) {
if (s == t) {
#define s id[s]
a[s] += k;
lep(i, lg(w[s]) + 1, V) sV[p][i] += 1ll * k * v[s], sW[p][i] += 1ll * k * w[s];
return;
#undef s
} d <= md ? mdy(d, s, md, k, ls) : mdy(d, md + 1, t, k, rs); pu(p);
}
ll qry(int s, int t, ll& c, int p) {
if (s == t) {
#define s id[s]
ll tot = std::min(a[s], c / w[s]); c -= tot * w[s];
return v[s] * tot;
#undef s
}
int i = lg(c);
if (i < V and c >= sW[p][i + 1]) { c -= sW[p][i + 1]; return sV[p][i + 1]; }
if (sW[p][i] <= c and c < tot[p][i]) { c -= sW[p][i]; return sV[p][i]; }
return qry(s, md, c, ls) + qry(md + 1, t, c, rs);
}
#undef ls
#undef rs
#undef md
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n >> q;
lep(i, 1, n) std::cin >> a[i] >> w[i] >> v[i], id[i] = i;
std::sort(id + 1, id + 1 + n, [](const int&x, const int&y) { return v[x] == v[y] ? w[x] < w[y] : v[x] > v[y]; });
lep(i, 1, n) ud[id[i]] = i;
bd(1, n, 1);
int op, d, k; ll c;
while (q--) {
std::cin >> op;
if (op == 1) std::cin >> k >> d, mdy(ud[d], 1, n, k, 1);
else if (op == 2) std::cin >> k >> d, mdy(ud[d], 1, n, -k, 1);
else std::cin >> c, std::cout << qry(1, n, c, 1) << '\n';
}
return 0;
}
P4755 Beautiful Pair
\(\boldsymbol{启发式分治}\) 。
注意到条件为 \(a_i\times a_j \le \max\{a_i\cdots a_j\}\)
最大值是不好维护的,所以我们枚举最大值。
考虑所有以当前值为最大值的区间。
枚举更短的一侧,固定一个端点,另一边的问题可以用主席树维护。
然后区间被划分成两个不相关的子问题。
复杂度 \(O(n\log^2 n)\) 。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 2e5 + 7;
const int V = 1e9;
typedef long long ll;
typedef double db;
typedef std::pair<int, int> PII;
int n, a[_], st[_][18], lg[_];
int rt[_], cnt[_ << 5], ls[_ << 5], rs[_ << 5], tot;
ll ans;
#define md ((s + t) >> 1)
void mdy(int d, int s, int t, int v, int& p) {
p = ++tot; ls[p] = ls[v], rs[p] = rs[v], cnt[p] = cnt[v] + 1;
if (s == t) return; d <= md ? mdy(d, s, md, ls[v], ls[p]) : mdy(d, md + 1, t, rs[v], rs[p]);
}
int qry(int d, int s, int t, int L, int R) {
if (t <= d) return cnt[R] - cnt[L];
return qry(d, s, md, ls[L], ls[R]) + (d > md ? qry(d, md + 1, t, rs[L], rs[R]) : 0);
}
#undef md
int upd(int u, int v) { return a[u] > a[v] ? u : v; }
void init() {
lep(j, 1, 17) lep(i, 1, n - (1 << j) + 1)
st[i][j] = upd(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
lep(i, 2, n) lg[i] = lg[i >> 1] + 1;
lep(i, 1, n) mdy(a[i], 1, V, rt[i - 1], rt[i]);
}
int get(int l, int r) { int k = lg[r - l + 1]; return upd(st[l][k], st[r - (1 << k) + 1][k]); }
void solve(int l, int r) {
if (l > r) return;
int p = get(l, r);
if (p - l < r - p)
lep(i, l, p) ans += qry(a[p] / a[i], 1, V, rt[p - 1], rt[r]);
else lep(i, p, r) ans += qry(a[p] / a[i], 1, V, rt[l - 1], rt[p]);
if (l == r) return; solve(l, p - 1), solve(p + 1, r);
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n;
lep(i, 1, n) std::cin >> a[i], st[i][0] = i;
init();
solve(1, n); std::cout << ans << '\n';
return 0;
}
At_agc001_e BBQ Hard
\(\boldsymbol{Ad-hoc}\) 。
上古好题。
考虑组合意义。
可以看做从 \((0, 0)\) 走到 \((a_i+a_j,b_i+b_j)\) ,只能向上或向右走的方案数。
但是这样还是和 \((i, j)\) 都有关,考虑平移。
变成 \((-a_i, -b_i)\) 走到 \((a_j, b_j)\) 的方案数,这样我们就拆开了 \(i\) 和 \(j\) 。
给每个负点位置赋初值,然后递推,在正点统计答案,然后容斥掉不需要的部分即可。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 8000 + 7;
const int __ = 2e5 + 7;
const int mod = 1e9 + 7;
const int V = 2000;
typedef long long ll;
typedef double db;
typedef std::pair<int, int> PII;
int n, a[__], b[__], f[_][_], ans, fac[_], inv[_];
int add(int u, int v) { return u + v >= mod ? u + v - mod : u + v; }
int mul(ll u, ll v) { return u * v >= mod ? u * v % mod : u * v; }
int MyPow(int a, int b) { int ans = 1; for (; b; b >>= 1, a = mul(a, a)) if (b & 1) ans = mul(ans, a); return ans; }
int C(int n, int m) { return mul(mul(fac[n], inv[m]), inv[n - m]); }
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n; fac[0] = 1;
lep(i, 1, 4 * V) fac[i] = mul(fac[i - 1], i);
inv[4 * V] = MyPow(fac[4 * V], mod - 2);
rep(i, 4 * V, 1) inv[i - 1] = mul(inv[i], i);
lep(i, 1, n) std::cin >> a[i] >> b[i], ++f[V - a[i]][V - b[i]];
lep(i, 0, 2 * V) lep(j, 0, 2 * V) {
if (i) f[i][j] = add(f[i][j], f[i - 1][j]);
if (j) f[i][j] = add(f[i][j], f[i][j - 1]);
}
lep(i, 1, n) ans = add(ans, f[V + a[i]][V + b[i]]), ans = add(ans, mod - C(2 * a[i] + 2 * b[i], 2 * a[i]));
ans = mul(ans, MyPow(2, mod - 2));
std::cout << ans << '\n';
return 0;
}
qoj#8049. Equal Sums
\(\boldsymbol{双射计数}\) 。
记录 \(f[i,j,k]\) 表示考虑到 \(a\) 的前缀 \(i\) , \(b\) 的前缀 \(j\) , \(\sum a - \sum b = k\) 的方案数。
发现值域太大了,做不了。
我们想到最后只需要 \(f[i,j,0]\) ,而它只与前面 \(f[i-1,j,-V\sim 0]\) 和 \(f[i,j-1,0\sim V]\) 有关。
但这并不能做,因为推前面的值还需要更多信息。
不过这仍然提醒我们要缩小值域,以及选择 \(a\) 会让 \(k\) 变大,选择 \(b\) 会让 \(k\) 变小。
现在想想如何刻画我们选择的过程。
我们钦定,如果 \(k\ge 0\) ,就从 \(b\) 选一个,否则,就从 \(a\) 选一个。
这样,每一种方案都会被刻画,因为每一种合法的选择方案都会被这样的策略数到恰好一次。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 500 + 7;
const int mod = 998244353;
const int V = 500;
typedef long long ll;
typedef double db;
typedef std::pair<int, int> PII;
int n, m, l[2][_], r[2][_], f[_][_][_ << 1];
int add(int u, int v) { return u + v >= mod ? u + v - mod : u + v; }
void upd(int& u, int v) { u = add(u, v); }
int mul(ll u, ll v) { return u * v >= mod ? u * v % mod : u * v; }
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n >> m;
lep(i, 1, n) std::cin >> l[0][i] >> r[0][i];
lep(i, 1, m) std::cin >> l[1][i] >> r[1][i];
f[0][0][V] = 1, f[0][0][V + 1] = -1;
lep(i, 0, n) lep(j, 0, m) {
lep(k, 1, 2 * V) upd(f[i][j][k], f[i][j][k - 1]);
if (i < n) {
lep(k, 0, V - 1) {
upd(f[i + 1][j][k + l[0][i + 1]], f[i][j][k]);
upd(f[i + 1][j][k + r[0][i + 1] + 1], mod - f[i][j][k]);
}
}
if (j < m) {
lep(k, V, 2 * V) {
upd(f[i][j + 1][k - r[1][j + 1]], f[i][j][k]);
upd(f[i][j + 1][k - l[1][j + 1] + 1], mod - f[i][j][k]);
}
}
}
lep(i, 1, n) {
lep(j, 1, m) std::cout << f[i][j][V] << ' ';
std::cout << '\n';
}
return 0;
}
Codeforces 1768F Wonderful Jump
\(\boldsymbol{根号分治优化 DP}\) 。
看到平方项以及值域,容易想到每次跳的不会很远。
那么具体是多远呢? 如果从 \(i\) 跳 \(len\) 到 \(j\) 比一步一步跳优,则一定满足:
\(\min \times len^2 \le \sum a \le n\times len\) ,即 \(\min \times len \le n\) 。
形式想到根号分治, \(len\le \sqrt n\) 直接暴力转移。
对于 \(\min \le \sqrt n\) ,我们再找到一个性质。
如果 \(i\) 跳到了 \(j\) ,那么 \(i\) 和 \(j\) 至少一个就是他们之中的最小值,否则,以最小值为中转一定会更优。
所以转移的端点一定是最小值。
使用单调栈维护之前最小值发生变化的位置,直接暴力扫栈,因为 \(\min \le \sqrt n\) ,所以栈内至多 \(\sqrt n\) 个元素。
注意 \(a_i\) 可能作为右端点的最小值,直接向左扫其能作为最小值的区间。
对于每一种数,以其为最小值的区间长度为 \(O(n)\) ,只有 \(\sqrt n\) 种数,所以均摊也是 \(O(n\sqrt n)\) 。
总复杂度 \(O(n\sqrt n)\) 。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 4e5 + 7;
typedef long long ll;
const ll inf = 1e17;
typedef double db;
typedef std::pair<int, int> PII;
int n, stk[_], tp; ll f[_], a[_];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n; int B = std::ceil(std::sqrt(n));
lep(i, 1, n) std::cin >> a[i]; stk[++tp] = 1;
lep(i, 2, n) {
ll mn = a[i], lim = std::max(1, i - B); f[i] = inf;
rep(j, i - 1, lim) mn = std::min(mn, a[j]), f[i] = std::min(f[i], f[j] + mn * (i - j) * (i - j));
while (tp and a[i] <= a[stk[tp]]) --tp;
lep(j, 1, tp) f[i] = std::min(f[i], f[stk[j]] + a[stk[j]] * (i - stk[j]) * (i - stk[j]));
if (a[i] > B) continue;
stk[++tp] = i;
rep(j, i - 1, 1) if (a[j] <= a[i]) break; else f[i] = std::min(f[i], f[j] + a[i] * (i - j) * (i - j));
}
lep(i, 1, n) std::cout << f[i] << ' '; std::cout << '\n';
return 0;
}
Atcoder ABC419_g Count Simple Paths 2
\(\boldsymbol{虚树,搜索}\) 。
注意到除去 \(dfs\) 树外最多有 \(21\) 条边。
建出这些边的端点以及点 \(n\) 的虚树,然后直接在虚树上暴力搜索。
复杂度 \(O(2^k k)\) , \(k\le 21\) 。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(G, i, u, t) for (int i = G.H[u], t = G.e[i].v; i; i = G.e[i].n, t = G.e[i].v)
const int _ = 2e5 + 7;
typedef long long ll;
typedef double db;
typedef std::pair<int, int> PII;
int n;
struct Graph {
struct edge { int v, n, w; }e[_ << 1]; int cnte = 1, H[_];
void add(int u, int v, int w = 0) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void Add(int u, int v, int w = 0) { add(u, v, w), add(v, u, w); }
}S, V;
int dfn[_], idx, dep[_], fa[_][21], m; bool vis[_];
int pr[_];
std::vector <PII> E;
std::vector <int> h;
int fnd(int x) { return pr[x] == x ? x : pr[x] = fnd(pr[x]); }
void mrg(int x, int y) {
if ((fnd(x)) == (fnd(y)))
{ h.push_back(x), h.push_back(y), E.push_back({x, y}); return; }
S.Add(x, y); pr[fnd(x)] = fnd(y);
}
void init(int u, int f) {
dfn[u] = ++idx, dep[u] = dep[fa[u][0] = f] + 1;
lep(i, 1, 18) fa[u][i] = fa[fa[u][i - 1]][i - 1];
ep(S, i, u, v) if (v != f) init(v, u);
}
int LCA(int x, int y) {
if (dep[x] < dep[y]) std::swap(x, y);
rep(i, 18, 0) if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
if (x == y) return x;
rep(i, 18, 0) if (fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
return fa[x][0];
}
int stk[_], tp;
void bd() { h.push_back(n);
std::sort(h.begin(), h.end()), h.erase(std::unique(h.begin(), h.end()), h.end());
std::sort(h.begin(), h.end(), [](int x, int y) { return dfn[x] < dfn[y]; });
stk[tp = 1] = 1; int l;
for (int i : h) {
l = LCA(stk[tp], i);
if (l != stk[tp]) {
while (tp > 1 and dep[stk[tp - 1]] > dep[l]) V.Add(stk[tp - 1], stk[tp], dep[stk[tp]] - dep[stk[tp - 1]]), --tp;
if (stk[tp - 1] == l) V.Add(l, stk[tp], dep[stk[tp]] - dep[l]), --tp;
else V.Add(l, stk[tp], dep[stk[tp]] - dep[l]), stk[tp] = l;
}
stk[++tp] = i;
}
lep(i, 1, tp - 1) V.Add(stk[i], stk[i + 1], dep[stk[i + 1]] - dep[stk[i]]);
for (auto t : E) V.Add(t.first, t.second, 1);
}
int ans[_];
void dfs(int u, int len) {
if (u == n) { ++ans[len]; return; }
vis[u] = true;
ep(V, i, u, v) if (!vis[v]) dfs(v, len + V.e[i].w);
vis[u] = false;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n >> m; int u, v;
lep(i, 1, n) pr[i] = i;
lep(i, 1, m) std::cin >> u >> v, mrg(u, v);
init(1, 0), bd(), dfs(1, 0);
lep(i, 1, n - 1) std::cout << ans[i] << ' ';
std::cout << '\n';
return 0;
}
BZOJ3864 Hero meet devil
\(\boldsymbol{dp 套 dp}\) 。
\(dp\) \(of\) \(dp\) 就是将一个有限状态自动机压入状态做 \(dp\) 。
可以用 \(AC\) 自动机之类的东西做类比。
对于这个题,记 \(f[i, g]\) 表示填了 \(i\) 个字符,最长公共子序列 \(dp\) 是 \(g\) 的方案数。
填一个字符就可以通过经典 \(DP\) 转移到 \(f[i+1, g']\) 。
现在考虑如何将 \(g\) 存下来。
发现 \(g\) 的每一位与前一位至多差 \(1\) ,所以可以将差分数组压成 \(01\) 状态存下来。
不理解的看代码。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define pc(S) __builtin_popcount(S)
const int _ = 5e4 + 7;
const int mod = 1e9 + 7;
typedef long long ll;
typedef double db;
typedef std::pair<int, int> PII;
int T, n, m, f[1001][_], r[_][4], t[20], c[20]; char s[20];
int ans[_];
int add(int u, int v) { return u + v >= mod ? u + v - mod : u + v; }
int calc(int g, int q) {
lep(i, 1, n) t[i] = t[i - 1] + ((g >> (i - 1)) & 1);
rep(i, n, 1) if (c[i] == q) t[i] = t[i - 1] + 1;
lep(i, 1, n) t[i] = std::max(t[i], t[i - 1]);
g = 0;
lep(i, 1, n) g |= (t[i] - t[i - 1]) << (i - 1);
return g;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> T;
while (T--) {
std::cin >> (s + 1) >> m; n = std::strlen(s + 1);
lep(i, 1, n) if (s[i] == 'A') c[i] = 0;
else if (s[i] == 'C') c[i] = 1;
else if (s[i] == 'G') c[i] = 2;
else if (s[i] == 'T') c[i] = 3;
int lim = (1 << n) - 1;
rep(i, lim, 0) lep(j, 0, 3) r[i][j] = calc(i, j);
std::memset(f, 0, sizeof(f));
f[0][0] = 1;
lep(i, 0, m - 1) lep(j, 0, lim) if (f[i][j]) lep(k, 0, 3) f[i + 1][r[j][k]] = add(f[i + 1][r[j][k]], f[i][j]);
lep(S, 0, lim) ans[pc(S)] = add(ans[pc(S)], f[m][S]);
lep(i, 0, n) std::cout << ans[i] << '\n', ans[i] = 0;
}
return 0;
}
P7603 [THUPC 2021] 鬼街
\(\boldsymbol{折半警报器}\) 。
(二进制警报器太巨了还没学会, %%% zak)
\(2\times 10^5\) 以内不同的质因子个数最多 \(6\) 个,是可以直接扫描的。
根据鸽巢原理,如果 \(\sum a\ge B\) ,且有 \(k\) 个房子,那么 \(\max a \ge \left\lceil\frac{B}{k} \right\rceil\) 。
所以,我们可以将每个警报器拆成 \(k\) 个小警报器放入每个房子,每个房子维护一个小根堆,每次取出堆顶判断是否达到阈值。
但这样还是太劣了,我们为什么要将阈值原样扔回去呢?
我们可以将 \(B-\Delta\) 作为 \(B'\) ,原本的报警器全部弃用,然后将 \(\left\lceil\frac{B'}{k} \right\rceil\) 再次放入相关的房子。
弃用的部分可以通过时间戳懒惰删除。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 2e5 + 7;
typedef long long ll;
typedef double db;
typedef std::pair<int, int> PII;
struct node { ll B; int t, id;
friend bool operator < (node x, node y) { return x.B > y.B; }
};
int n, m, last, seq[_]; bool np[_]; std::vector <int> P;
std::vector <int> ans, pos[_]; int tim[_], tot[_];
ll sum[_], All, lim[_], lst[_]; std::priority_queue <node> q[_];
void ins(int u) { ++tim[u], lst[u] = 0; for (int v : pos[u]) q[v].push({(lim[u] + tot[u] - 1) / tot[u] + sum[v], tim[u], u}), lst[u] += sum[v]; }
void add(int u, ll k) {
sum[u] += k;
while (!q[u].empty()) {
auto t = q[u].top();
if (t.t < tim[t.id]) { q[u].pop(); continue; }
if (t.B <= sum[u]) {
int x = t.id; lim[x] += lst[x]; q[u].pop();
for (int v : pos[x]) lim[x] -= sum[v];
if (lim[x] <= 0) ans.push_back(x), tim[x] = 1e9;
else ins(x); continue;
}
break;
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n >> m;
lep(i, 2, n) {
if (!np[i]) P.push_back(i), seq[i] = i;
for (int j : P) if (i * j <= n) {
np[i * j] = true, seq[i * j] = j;
if (i % j == 0) break;
} else break;
}
int op, x, idx = 0, c; ll y;
while (m--) {
std::cin >> op >> x >> y; y ^= last;
if (op == 0) {
while (x > 1) {
c = seq[x], add(c, y);
while (x % c == 0) x /= c;
}
std::sort(ans.begin(), ans.end());
std::cout << (last = ans.size()) << ' ';
for (int v : ans) std::cout << v << ' ';
std::cout << '\n'; ans.clear();
}
else { ++idx;
if (!y) { ans.push_back(idx); continue; }
lim[idx] = y;
while (x > 1) {
c = seq[x], pos[idx].push_back(c);
while (x % c == 0) x /= c;
}
tot[idx] = pos[idx].size(), ins(idx);
}
}
return 0;
}
P7962 [NOIP2021] 方差
\(\boldsymbol{DP}\) 。
操作等价于交换方差数组,首项不能交换,但是根据方差定义,全部元素减去首项,方差不变。
所以可以直接将首项置 \(0\) ,我们可以将 \(n-1\) 项差分数组任意交换。
记 \(d_i=a_{i+1}-a_i\) ,需要最小化:
发现,每项乘积的系数是一个关于位置的单峰函数,所以差分数组的最优情况一定是单谷的。(感性理解)
所以我们就可以将差分数组排序,并按照如下形式 \(DP\) 。
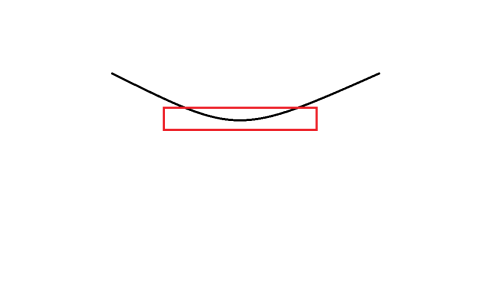
依次将差分数组放在红色框的两侧,维护 \(f[i, x]\) 表示考虑了前 \(i\) 项,\(\sum a\) 的值为 \(x\) 时,\(\sum a^2\) 的最小值。
记 \(s_i=\sum_{j=1}^id_j\)
新的差分放在左侧, \(f[i+1][x+i\cdot d_i]\leftarrow f[i, x] + i\cdot d_i^2+2dx\) 。
放在右侧, \(f[i+1,x+s_i]\leftarrow f[i, x] + s_i^2\) 。
滚动数组优化空间,当 \(d_i=0\) 时直接忽略。
空间复杂度 \(O(n\cdot a)\) ,时间复杂度 \(O(na\cdot \min(n, a))\) 。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define cmx(x, y) std::max(x, y)
#define cmn(x, y) std::min(x, y)
#define gmx(x, y) x = std::max(x, y)
#define gmn(x, y) x = std::min(x, y)
const int _ = 1e4 + 7;
typedef double Db;
typedef long long ll;
typedef std::pair<int, int> PII;
const ll inf = 1e16;
int n, a[_], lim; ll d[_], f[2][_ * 1000], s[_];
int main() {
std::ios::sync_with_stdio(false),
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n; int mx = 0, p = 0;
lep(i, 1, n) std::cin >> a[i], mx = std::max(mx, a[i]);
lep(i, 1, n - 1) a[i] = a[i + 1] - a[i];
std::sort(a + 1, a + n);
lim = n * mx;
lep(i, 1, lim) f[p][i] = inf;
lep(i, 1, n - 1) if (a[i]) { s[i] = s[i - 1] + a[i];
lep(x, 0, lim) f[p ^ 1][x] = inf;
rep(x, lim, 0) if (f[p][x] != inf) {
gmn(f[p ^ 1][x + 1ll * i * a[i]], f[p][x] + 1ll * i * a[i] * a[i] + 2ll * a[i] * x),
gmn(f[p ^ 1][x + s[i]], f[p][x] + s[i] * s[i]);
}
p ^= 1;
}
ll ans = inf;
lep(i, 1, lim) gmn(ans, n * f[p][i] - 1ll * i * i);
std::cout << ans << '\n';
return 0;
}
P7916 [CSP-S 2021] 交通规划
不怎么会严谨的证明通法。
首先对于 \(k=2\) 的情况,如果两个点颜色不同,整张图一定会被染成黑白两个连通块,而代价即为中间分割线的部分。
可以看成最小割,那么就可以看做对偶图上的最短路。
当 \(k>2\) 时,可以将不同的关键点之间分块,一个块的端点颜色不同时视作一个待处理块。
一定会有偶数个待处理块,最后的合法方案即为块之间两两不交配对后,最短路径经过的边权和。
预处理块之间的最短路,然后平凡的区间 \(DP\) 求解。
点击查看代码
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define cmx(x, y) std::max(x, y)
#define cmn(x, y) std::min(x, y)
#define gmx(x, y) x = std::max(x, y)
#define gmn(x, y) x = std::min(x, y)
template < typename T >
void _debug(const T &t) { std::cerr << t << '\n'; }
template < typename T, typename... Args>
void _debug(const T &t, const Args &...rest) {
std::cerr << t << ' ';
_debug(rest...);
}
#define debug(...) _debug(#__VA_ARGS__ " =", __VA_ARGS__)
typedef double Db;
typedef long long ll;
typedef std::pair<ll, int> PLI;
const int _ = 2e6 + 7;
const ll inf = 1e17;
struct node { int x, v, c; };
struct edge { int v, n, w; }e[_]; int H[_], cnte = 1;
int n, m, qy, ec[_], pc[_]; ll g[500][500], f[500][500], dis[_];
std::vector <node> ls; std::bitset<_> vis;
std::vector <int> rs;
void add(int u, int v, int w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void Add(int u, int v, int w) { add(u, v, w), add(v, u, w); }
int id(int x, int y) { return x * (m + 1) + y; }
void init() {
int v;
lep(i, 1, n - 1) lep(j, 1, m) std::cin >> v, Add(id(i, j - 1), id(i, j), v);
lep(i, 1, n) lep(j, 1, m - 1) std::cin >> v, Add(id(i - 1, j), id(i, j), v);
lep(i, 1, m - 1) Add(pc[i] = id(0, i), id(0, i + 1), 0), ec[i + 1] = (cnte >> 1);
lep(i, m, m + n - 1) Add(pc[i] = id(i - m, m), id(i - m + 1, m), 0), ec[i + 1] = (cnte >> 1);
lep(i, m + n, 2 * m + n - 1) Add(pc[i] = id(n, 2 * m + n - i), id(n, 2 * m + n - i - 1), 0), ec[i + 1] = (cnte >> 1);
lep(i, 2 * m + n, 2 * m + 2 * n - 1) Add(pc[i] = id(2 * m + 2 * n - i, 0), id(2 * m + 2 * n - i - 1, 0), 0), ec[i + 1] = (cnte >> 1);
Add(pc[2 * n + 2 * m] = id(0, 0), id(0, 1), 0), ec[1] = (cnte >> 1);
}
void upd(int x, int v) { e[ec[x] << 1].w = e[ec[x] << 1 | 1].w = v; }
void cls() { rep(i, 2 * m + 2 * n, 1) upd(i, 0); }
void dij(int s) { std::priority_queue <PLI> d;
rep(i, n * (m + 1) + m, 0) dis[i] = inf, vis[i] = false;
dis[s] = 0, d.push({0, s}); int u, w;
while (!d.empty()) {
u = d.top().second; d.pop();
if (vis[u]) continue; vis[u] = true;
for (int i = H[u], v = e[i].v; i; i = e[i].n, v = e[i].v) { w = e[i].w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w, d.push({-dis[v], v});
}
}
}
}
int main() {
std::ios::sync_with_stdio(false),
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n >> m >> qy;
init();
int k, x, v, c;
while (qy--) {
std::cin >> k; ls.clear(), rs.clear(), rs.push_back(0);
lep(i, 1, k) std::cin >> v >> x >> c, ls.push_back({x, v, c}), upd(x, v);
if (k == 1) { std::cout << "0\n", cls(); continue; }
std::sort(ls.begin(), ls.end(), [](const node& x, const node& y) { return x.x < y.x; });
lep(t, 1, k - 1) if (ls[t].c != ls[t - 1].c) rs.push_back(pc[ls[t - 1].x]);
if (ls[0].c != ls[k - 1].c) rs.push_back(pc[ls[k - 1].x]);
k = rs.size() - 1;
if (k <= 1) { std::cout << "0\n", cls(); continue; }
lep(i, 1, k) {
dij(rs[i]);
lep(j, 1, k) g[i][j] = g[i][j + k] = g[i + k][j] = g[i + k][j + k] = dis[rs[j]];
rs.push_back(rs[i]);
}
int r;
for (int len = 2; len <= k; len += 2) lep(l, 1, 2 * k - len + 1) { r = l + len - 1;
f[l][r] = inf;
for (int k = l + 1; k <= r; k += 2)
gmn(f[l][r], f[l + 1][k - 1] + g[l][k] + f[k + 1][r]);
}
ll ans = inf;
lep(i, 1, k) gmn(ans, f[i][i + k - 1]);
std::cout << ans << '\n'; cls();
}
return 0;
}
时间仓促,如有错误欢迎指出,欢迎在评论区讨论,如对您有帮助还请点个推荐、关注支持一下

 八月训练好题记录
八月训练好题记录

 浙公网安备 33010602011771号
浙公网安备 33010602011771号