MX galaxy Day11
P3749 [六省联考 2017] 寿司餐厅
\(\boldsymbol{最大权闭合子图}\) 。
将每个区间作为点,每个区间选了其子区间一定要选。
对于 \(cx\) ,将每个长度为 \(1\) 的区间的贡献减去那种颜色的编号,然后正常处理即可。
至于 \(mx^2\) ,我们将每个点向一个代表其颜色的虚点连边,虚点向汇点连 \(mx^2\) 的边。
意味着,只要有一个点与源点连通,就需要耗费 \(mx^2\) 的代价。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 3e6 + 7;
const int __ = 1e3;
typedef long long ll;
typedef std::pair<int, int> PII;
const ll inf = 1e18;
struct edge { int v, n; ll c; }e[_]; int H[_], cur[_], cnte = 1;
int n, m, a[_], dep[_], s, t, idx, d[__][__]; ll ans;
std::map<PII, int> Nam;
void Add(int u, int v, ll c) { if (u == s) ans += c; e[++cnte] = { v, H[u], c }, H[u] = cnte, e[++cnte] = { u, H[v], 0 }, H[v] = cnte; }
bool bfs() { std::queue <int> q;
lep(i, 1, idx) dep[i] = 0;
dep[s] = 1, q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
if (u == t) return true;
for (int i = H[u], v = e[i].v; i; i = e[i].n, v = e[i].v)
if (!dep[v] and e[i].c > 0) dep[v] = dep[u] + 1, q.push(v);
}
return false;
}
ll dfs(int u, ll total) {
if (u == t or !total) return total;
ll res = 0, f;
for (int i = cur[u], v = e[i].v; i; i = e[i].n, v = e[i].v) { cur[u] = i;
if (e[i].c > 0 and dep[v] == dep[u] + 1)
f = dfs(v, std::min(total, e[i].c)),
e[i].c -= f, e[i ^ 1].c += f, res += f, total -= f;
}
return res;
}
void Dinic() {
while (bfs()) {
lep(i, 1, idx) cur[i] = H[i];
ans -= dfs(s, inf);
}
}
int Id(int x, int y) { return Nam[{x, y}] ? Nam[{x, y}] : Nam[{x, y}] = ++idx; }
void Init() {
s = ++idx, t = ++idx;
lep(i, 1, n) lep(j, i + 1, n) {
if (d[i][j] >= 0) Add(s, Id(i, j), d[i][j]);
else Add(Id(i, j), t, -d[i][j]);
Add(Id(i, j), Id(i + 1, j), inf), Add(Id(i, j), Id(i, j - 1), inf);
}
lep(i, 1, n) { ll w = d[i][i] - a[i];
if (w >= 0) Add(s, Id(i, i), w);
else Add(Id(i, i), t, -w);
Add(Id(i, i), Id(n + 1, a[i]), inf);
}
lep(i, 1, 1000) Add(Id(n + 1, i), t, 1ll * m * i * i);
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, n) scanf("%d", a + i);
lep(i, 1, n) lep(j, i, n) scanf("%d", d[i] + j);
Init(), Dinic();
printf("%lld\n", ans);
return 0;
}
P4313 文理分科
将每个点与限制相关的连通块按照黑白分开。
转换成最小割模型。
将每个白点向互斥的黑点连 \(inf\) 边,每个白色连通块向互斥的黑点连 \(inf\) 边。
每个白点向互斥的黑色连通块连 \(inf\) 边,每个白色连通块向互斥的黑色连通块连 \(inf\) 边。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ABS(x) ((x) > 0 ? (x) : -(x))
const int _ = 3e6 + 7;
const int __ = 100 + 7;
const int inf = 2e9;
typedef long long ll;
typedef std::pair<int, int> PII;
struct edge { int v, n, c; }e[_]; int H[_], cur[_], cnte = 1;
int n, m, dep[_], s, t, idx; ll ans;
int a[__][__], b[__][__], A[__][__], B[__][__];
int di[5] = { 0, 0, 0, 1, -1 };
int dj[5] = { 1, -1, 0, 0, 0 };
int Di[13] = { 0, 0, 0, 1, 1, 1, -1, -1, -1, 0, 0, 2, -2 };
int Dj[13] = { 0, 1, -1, 0, 1, -1, 0, 1, -1, 2, -2, 0, 0 };
std::map<PII, int> Nam;
void Add(int u, int v, int c) { e[++cnte] = { v, H[u], c }, H[u] = cnte, e[++cnte] = { u, H[v], 0 }, H[v] = cnte; }
bool bfs() { std::queue <int> q;
lep(i, 1, idx) dep[i] = 0;
dep[s] = 1, q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
if (u == t) return true;
for (int i = H[u], v = e[i].v; i; i = e[i].n, v = e[i].v)
if (!dep[v] and e[i].c > 0) dep[v] = dep[u] + 1, q.push(v);
}
return false;
}
int dfs(int u, int total) {
if (u == t or !total) return total;
int res = 0, f;
for (int i = cur[u], v = e[i].v; i; i = e[i].n, v = e[i].v) { cur[u] = i;
if (e[i].c > 0 and dep[v] == dep[u] + 1) {
f = dfs(v, std::min(total, e[i].c));
if (!f) { dep[v] = 0; continue; }
e[i].c -= f, e[i ^ 1].c += f, res += f, total -= f;
if (!total) break;
}
}
return res;
}
void Dinic() {
while (bfs()) {
lep(i, 1, idx) cur[i] = H[i];
ans -= dfs(s, inf);
}
}
int Id(int op, int x, int y) { return op * n * m + (x - 1) * m + y; }
void Init() {
s = 4 * n * m + 1, t = idx = s + 1;
lep(x, 1, n) lep(y, 1, m) {
Add(s, Id(0, x, y), a[x][y]), Add(Id(1, x, y), t, b[x][y]);
Add(Id(0, x, y), Id(1, x, y), inf);
Add(s, Id(2, x, y), A[x][y]), Add(Id(3, x, y), t, B[x][y]);
lep(k, 0, 4) { int dx = x + di[k], dy = y + dj[k];
if (dx < 1 or dy < 1 or dx > n or dy > m) continue;
Add(Id(0, x, y), Id(3, dx, dy), inf),
Add(Id(2, x, y), Id(1, dx, dy), inf);
}
lep(k, 0, 12) { int dx = x + Di[k], dy = y + Dj[k];
if (dx < 1 or dy < 1 or dx > n or dy > m) continue;
Add(Id(2, x, y), Id(3, dx, dy), inf);
}
}
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, n) lep(j, 1, m) scanf("%d", a[i] + j), ans += a[i][j];
lep(i, 1, n) lep(j, 1, m) scanf("%d", b[i] + j), ans += b[i][j];
lep(i, 1, n) lep(j, 1, m) scanf("%d", A[i] + j), ans += A[i][j];
lep(i, 1, n) lep(j, 1, m) scanf("%d", B[i] + j), ans += B[i][j];
Init(), Dinic();
printf("%lld\n", ans);
return 0;
}
P9879 [EC Final 2021] Check Pattern is Good
容易发现网格图是个二分图,可以将其进行黑白染色。
将每个黑色点的位置的 W , B 翻转,那么产生贡献的连通块形如:
\[\begin{matrix}
WW\\
WW
\end{matrix}
\]
或者
\[\begin{matrix}
BB\\
BB
\end{matrix}
\]
类似上一题建模即可。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u) for (int i = H[u], v = e[i].v; i ; i = e[i].n, v = e[i].v)
typedef long long ll;
const int _ = 1e6 + 7;
const int inf = 2e9;
struct edge { int v, n, c; }e[_]; int H[_], cur[_], cnte = 1;
int T, n, m, s, t, val[110][110], dep[_], ans;
char c[_];
int di[9] = { 0, -1, 1, 0, -1, 1, 0, -1, 1 };
int dj[9] = { 0, -1, 1, -1, 1, 0, 1, 0, -1 };
int id(int k, int x, int y) { return k * (n - 1) * (m - 1) + (x - 1) * (m - 1) + y; }
void Add(int u, int v, int c) { if (c != inf) ans += c; e[++cnte] = { v, H[u], c }, H[u] = cnte; }
bool Bfs() { std::queue <int> d;
lep(i, s, t) dep[i] = 0, cur[i] = H[i]; dep[s] = 1;
d.push(s);
while (!d.empty()) {
int u = d.front(); d.pop();
ep(i, u) if (e[i].c > 0 and !dep[v]) {
dep[v] = dep[u] + 1;
d.push(v);
if (v == t) return true;
}
}
return false;
}
int Dfs(int u, int want) {
if (u == t) return want;
int tot = 0, flow;
for (int i = cur[u], v = e[i].v; i and want; i = e[i].n, v = e[i].v) { cur[u] = i;
if (e[i].c > 0 and dep[v] == dep[u] + 1) {
flow = Dfs(v, std::min(want, e[i].c));
e[i].c -= flow, e[i ^ 1].c += flow,
tot += flow, want -= flow;
}
}
return tot;
}
int main() {
scanf("%d", & T);
while (T--) {
scanf("%d%d", & n, & m);
lep(i, 1, n) {
scanf("%s", c + 1);
lep(j, 1, m) {
if (c[j] == '?') val[i][j] = -1;
else val[i][j] = ((c[j] == 'B') ^ ((i + j) & 1));
}
}
s = 0, t = 2 * (n - 1) * (m - 1) + 1;
lep(i, 1, n - 1) lep(j, 1, m - 1) {
bool f0 = false, f1 = false;
lep(k, 0, 1) lep(t, 0, 1) {
if (val[i + k][j + t] == 0) f0 = true;
if (val[i + k][j + t] == 1) f1 = true;
}
if (!f1) Add(s, id(0, i, j), !f1), Add(id(0, i, j), s, 0);
if (!f0) Add(id(1, i, j), t, !f0), Add(id(1, i, j), s, 0);
lep(k, 0, 8) {
int dx = i + di[k], dy = j + dj[k];
if (dx and dy and dx < n and dy < m)
Add(id(0, i, j), id(1, dx, dy), inf),
Add(id(1, dx, dy), id(0, i, j), 0);
}
}
while (Bfs()) ans -= Dfs(s, inf);
lep(i, 1, n - 1) lep(j, 1, m - 1) {
if (dep[id(0, i, j)])
val[i][j] = val[i + 1][j] = val[i][j + 1] = val[i + 1][j + 1] = 0;
}
lep(i, 1, n) lep(j, 1, m) val[i][j] = (((~val[i][j] ? val[i][j] : 1) ^ (i + j)) & 1);
printf("%d\n", ans); ans = 0;
lep(i, 1, n) {
lep(j, 1, m) putchar(val[i][j] ? 'B' : 'W');
putchar('\n');
}
lep(i, s, t) H[i] = 0; cnte = 1;
}
return 0;
}
P3227 [HNOI2013] 切糕
\(\boldsymbol{切糕模型}\) 。
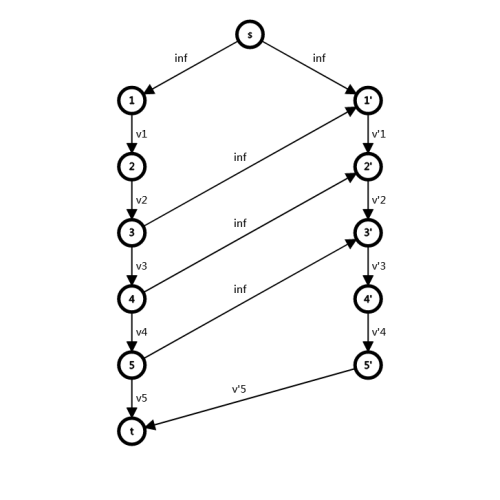
如图建模,割掉那条边,就意味着值域选哪个数。
对于每个限制,拆成 \(b-d\le a \le b+d\) ,对于当前值域链,只考虑大于等于的部分。
如图为 \(d=2\) 时的连边。
来看 \(4\) 和 \(2'\) 两个点,意味着如果 \(v4\) 被选了,那么另一条链一定要选一个大于等于 \(v'2\) 的数。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ABS(x) ((x) > 0 ? (x) : -(x))
const int _ = 3e6 + 7;
const int __ = 100 + 7;
const int inf = 2e9;
typedef long long ll;
typedef std::pair<int, int> PII;
struct edge { int v, n, c; }e[_]; int H[_], cur[_], cnte = 1;
int n, m, c, d, dep[_], s, t, ans;
int v[__][__][__];
int di[4] = { 0, 0, 1, -1 };
int dj[4] = { 1, -1, 0, 0 };
void Add(int u, int v, int c) { e[++cnte] = { v, H[u], c }, H[u] = cnte, e[++cnte] = { u, H[v], 0 }, H[v] = cnte; }
bool bfs() { std::queue <int> q;
lep(i, s, t) dep[i] = 0;
dep[s] = 1, q.push(s);
while (!q.empty()) {
int u = q.front(); q.pop();
if (u == t) return true;
for (int i = H[u], v = e[i].v; i; i = e[i].n, v = e[i].v)
if (!dep[v] and e[i].c > 0) dep[v] = dep[u] + 1, q.push(v);
}
return false;
}
int dfs(int u, int total) {
if (u == t or !total) return total;
int res = 0, f;
for (int i = cur[u], v = e[i].v; i and total; i = e[i].n, v = e[i].v) { cur[u] = i;
if (e[i].c > 0 and dep[v] == dep[u] + 1) {
f = dfs(v, std::min(total, e[i].c));
if (!f) { dep[v] = 0; continue; }
e[i].c -= f, e[i ^ 1].c += f, res += f, total -= f;
}
}
return res;
}
void Dinic() {
while (bfs()) {
lep(i, s, t) cur[i] = H[i];
ans += dfs(s, inf);
}
}
int Id(int x, int y, int z) { return (z - 1) * n * m + (x - 1) * m + y; }
void Init() {
s = 0, t = Id(n, m, c) + 1;
lep(x, 1, n) lep(y, 1, m) {
Add(s, Id(x, y, 1), inf);
lep(r, 1, c - 1) Add(Id(x, y, r), Id(x, y, r + 1), v[x][y][r]);
Add(Id(x, y, c), t, v[x][y][c]);
lep(k, 0, 3) { int dx = x + di[k], dy = y + dj[k];
if (dx < 1 or dy < 1 or dx > n or dy > m) continue;
lep(r, d + 1, c) Add(Id(x, y, r), Id(dx, dy, r - d), inf);
}
}
}
int main() {
scanf("%d%d%d%d", & n, & m, & c, & d);
lep(z, 1, c) lep(x, 1, n) lep(y, 1, m)
scanf("%d", v[x][y] + z);
Init(), Dinic();
printf("%d\n", ans);
return 0;
}
时间仓促,如有错误欢迎指出,欢迎在评论区讨论,如对您有帮助还请点个推荐、关注支持一下

 网络流模型
网络流模型

 浙公网安备 33010602011771号
浙公网安备 33010602011771号