数据结构 - 李超线段树

概述

李超线段树实现了这样的一个功能，通过类似标记永久化的思想，维护一个二维平面上的一些直线或线段的信息。
一般是某处的最大/小取值。

实现

（以 模板题 为例）
李超线段树的每个节点都存储了一条线段作为标记，表示完全覆盖当前区间的标记线段中，中点取值最大的一条。

插入

先假设我们要插入一条全局的直线，且根节点本来就存有一条直线。

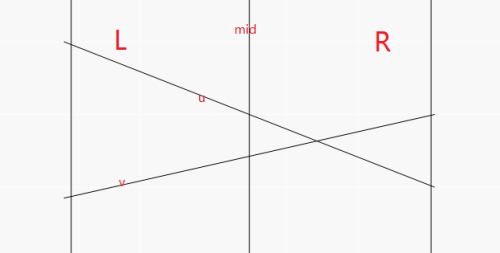
将中点更优的直线记作 \(u\) ，另一条直线记作 \(v\) ，则 \(u\) 应该作为标记保留在当前节点，而 \(v\) 应该将自己下传。
如上图，\(v\) 在右区间内仍有可能作为最大值，所以应下传到右区间，而右区间可能本来就存在一条标记，递归下传即可。
细节上，可以将插入线段和原本的标记比较，如果更优就交换，下传那个不优的线段。

每次只会选择一侧下传，时间复杂度是 \(O(\log n)\) 的。

如果插入的是一条线段呢，先花费 \(O(\log n)\) 的代价定位完全覆盖的区间，然后按照上述描述比较、下传标记即可。
复杂度 \(O(\log^2 n)\) 。

查询

容易发现，每个节点存储的并非是全局中点取值最大的线段，因为那可能在它的父亲节点中。
按照中点值的大小下传，只是为了将线段分类，只保留可能作为答案的那些线段。

所以查询也很简单了，定位到叶子节点，到根路径上的每一个节点的标记取最优即可。

代码

Db pt(int x, int d) { return k[x] * d + b[x]; }
int upd(int x, int y, int k) {
	Db dl = pt(x, k) - pt(y, k);
	if (std::fabs(dl) < eps) return std::min(x, y);
	if (dl > 0) return x; return y;
}
#define ls p << 1
#define rs p << 1 | 1
#define md ((s + t) >> 1)
void mdy(int s, int t, int v, int p) { int& u = id[p];
	if (upd(u, v, md) == v) std::swap(u, v);
	if (s == t) return;
	if (upd(u, v, s) == v) mdy(s, md, v, ls);
	if (upd(u, v, t) == v) mdy(md + 1, t, v, rs);
}
void ins(int l, int r, int s, int t, int v, int p) {
	if (l <= s and t <= r) return mdy(s, t, v, p);
	if (l <= md) ins(l, r, s, md, v, ls);
	if (r > md) ins(l, r, md + 1, t, v, rs);
}
int qry(int d, int s, int t, int p) {
	if (s == t) return id[p];
	return upd(id[p], d <= md ? qry(d, s, md, ls) : qry(d, md + 1, t, rs), d);
}

例题

李超线段树不单独出现，一般都用来优化算法，比如斜率优化。
此处不放出例题，读者可自行百度。
笔者有时间可能会来补，可能吧……