MX galaxy Day4

tree

拆式子可以获得一个维护 \(siz\) 和 \(siz \times (w_u - w_{fa_u})\) 的树剖 + 线段树做法。
不过我并没有这么做。
每次新加入一个点，发现到根路径上是这样的一个贡献。

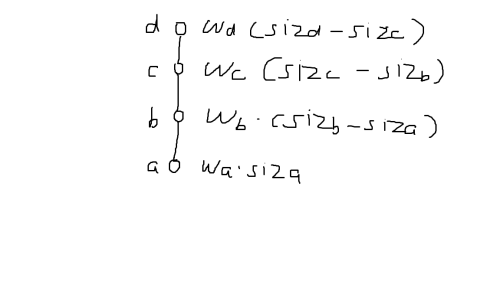
将 \(siz\) 提出来，变成了这样的式子。

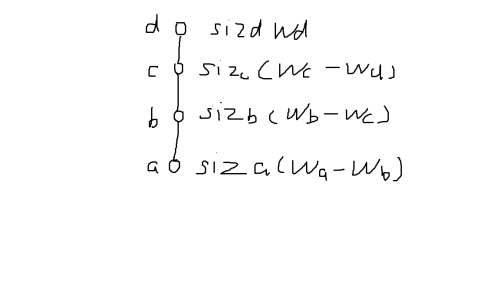
每次加入节点会让到根路径上点权值增加 \(w_u - w_{fa_u}\) ，总答案累加上他们的权值，吉司机线段树即可。

Info : \(ans\) 答案， \(sum\) 当前权值， \(val\) 差分后的权值。
Tag : \(ans += sum * ts + val * tav\) , \(sum += val * tv\) 。

双半群模型维护即可。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 2e5 + 7;
typedef long long ll;

struct Info {
	ll ans, sum, val; int l, r;
	Info(ll _ans = 0, ll _sum = 0, ll _val = 0, int _l = 0, int _r = 0) { ans = _ans, sum = _sum, val = _val, l = _l, r = _r; }
	friend Info operator + (const Info& x , const Info& y) { return Info(x.ans + y.ans, x.sum + y.sum, x.val + y.val, x.l, y.r); }
}tr[_ << 2];
struct Tag {
	ll tv, ts, tav;
	Tag(ll _tv = 0, ll _ts = 0, ll _tav = 0) { tv = _tv, ts = _ts, tav = _tav; }
	friend Tag operator + (const Tag& x, const Tag& y) { return Tag(x.tv + y.tv, x.ts + y.ts, x.tav + y.tav + x.tv * y.ts); }
	bool ne() { return tv or ts or tav; }
}tag[_ << 2];
Info operator * (const Info& x, const Tag& y) { return Info(x.ans + x.sum * y.ts + x.val * y.tav, x.sum + x.val * y.tv, x.val, x.l, x.r); }
int q, n; ll w[_], a[_];
int idx, dfn[_], top[_], sz[_], son[_], fa[_];
std::vector <int> o;
std::vector <int> e[_];

#define ls p << 1
#define rs p << 1 | 1
void pu(int p) { tr[p] = tr[ls] + tr[rs]; }
void upd(int p, const Tag& k) { tr[p] = tr[p] * k, tag[p] = tag[p] + k; }
void pd(int p) { if (tag[p].ne()) upd(ls, tag[p]), upd(rs, tag[p]), tag[p] = Tag(); }
void Build(int l, int r, int p) {
	if (l == r) { tr[p] = { 0, 0, a[l], l, l }; return; } int mid = (l + r) >> 1;
	Build(l, mid, ls), Build(mid + 1, r, rs); pu(p);
}
void mdy(int l, int r, const Tag& k, int p) {
	if (r < tr[p].l or tr[p].r < l) return;
	if (l <= tr[p].l and tr[p].r <= r) return upd(p, k); pd(p);
	mdy(l, r, k, ls), mdy(l, r, k, rs); pu(p);
}
#undef ls
#undef rs
ll Qry() { return tr[1].ans; }
void Init(int u) {
	sz[u] = 1;
	for (int v : e[u]) {
		Init(v), sz[u] += sz[v];
		if (sz[v] > sz[son[u]]) son[u] = v;
	}
	w[u] -= w[fa[u]];
}
void Init(int u, int tp) {
	dfn[u] = ++idx, a[idx] = w[u], top[u] = tp;
	if (!son[u]) return; Init(son[u], tp);
	for (int v : e[u]) if (v != son[u]) Init(v, v);
}
void Jump(int x) {
	while (x) {
		mdy(dfn[top[x]], dfn[x], { 1, 1, 1 }, 1);
		x = fa[top[x]];
	}
}

int main() {

	freopen("tree.in", "r", stdin);
	freopen("tree.out","w",stdout);

	scanf("%d%lld", & q, w + 1); n = 1;
	o.push_back(1);

	int op;
	while (q--) {
		scanf("%d", & op);
		if (op == 1) ++n, scanf("%lld%d", w + n, fa + n), e[fa[n]].push_back(n), o.push_back(n);
		else o.push_back(0);
	}
	Init(1), Init(1, 1); Build(1, n, 1);

	for (int k : o) {
		if (k) Jump(k);
		else printf("%lld\n", Qry());
	}
	return 0;
}

bulb

根号分治模板。
\(1\) 的联通段个数 = \(1\) 的数量 - 相邻 \(1\) 的个数。

前者可以直接算。
按照出现次数将颜色分为重颜色和轻颜色。
轻颜色直接暴力修改，重颜色可以维护和这种颜色相邻的不同颜色的个数。
将轻颜色对重颜色的贡献打包计算。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 2e5 + 7;
typedef long long ll;

int n, q, k, c[_], tot[_], id[_], ans, len; bool bg[_], lt[_];
int cnt[600], neb[600][600]; //this -> others
std::vector <int> B;
std::vector <int> pos[_];

void Add(int p) {
	if (p > 1) {
		if (lt[c[p - 1]]) --ans;
		if (bg[c[p - 1]]) ++cnt[id[c[p - 1]]];
	}
	if (p < n) {
		if (lt[c[p + 1]] and c[p + 1] != c[p]) --ans;
		if (bg[c[p + 1]]) ++cnt[id[c[p + 1]]];
	}
}
void Del(int p) {
	if (p > 1) {
		if (lt[c[p - 1]]) ++ans;
		if (bg[c[p - 1]]) --cnt[id[c[p - 1]]];
	}
	if (p < n) {
		if (lt[c[p + 1]] and c[p + 1] != c[p]) ++ans;
		if (bg[c[p + 1]]) --cnt[id[c[p + 1]]];
	}
}

int main() {
#ifndef DEBUG
	freopen("bulb.in", "r", stdin);
	freopen("bulb.out","w",stdout);
#endif
	scanf("%d%d%d", & n, & q, & k);
	lep(i, 1, n) scanf("%d", c + i), ++tot[c[i]];
	lep(i, 1, k) if (tot[i] > std::sqrt(n)) bg[i] = true;
	B.push_back(0);
	lep(i, 1, n) {
		if (bg[c[i]] and !id[c[i]]) id[c[i]] = ++len, B.push_back(c[i]);
		if (!bg[c[i]]) pos[c[i]].push_back(i);
	}
	lep(i, 2, n) if (bg[c[i]] and bg[c[i - 1]]) {
		++neb[id[c[i]]][id[c[i - 1]]];
		if (c[i] != c[i - 1]) ++neb[id[c[i - 1]]][id[c[i]]];
	}

	int x;
	while (q--) {
		scanf("%d", & x);
		if (lt[x]) ans -= tot[x];
		else ans += tot[x];
		if (bg[x]) {
			if (lt[x]) {
				ans += cnt[id[x]];
				lep(i, 1, len) if (lt[B[i]]) ans += neb[id[x]][i];
				lt[x] ^= 1;
			}
			else {
				ans -= cnt[id[x]]; lt[x] ^= 1;
				lep(i, 1, len) if (lt[B[i]]) ans -= neb[id[x]][i];
			}
		}
		else {
			if (lt[x]) { for (int k : pos[x]) Del(k); lt[x] ^= 1; }
			else { lt[x] ^= 1; for (int k : pos[x]) Add(k); }
		}
		printf("%d\n", ans);
	}
	return 0;
}

beehive

读题。
发现答案为 总点数 - 割边数。
构造方案为，将所有的点和边选上，每次去掉一条非割边，最后求交。
就得到了割边数的两元连通块和很多孤立点。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 4e5 + 7;
typedef long long ll;

struct edge { int v, n; }e[_]; int H[_], cnte = 1;
int n, m, dfn[_], low[_], idx, stk[_], top, scc; bool vis[_];

void Add(int u, int v) { e[++cnte] = { v, H[u] }, H[u] = cnte; }
void Tarjan(int u) {
	dfn[u] = low[u] = ++idx, stk[++top] = u;
	for (int i = H[u], v = e[i].v; i; i = e[i].n, v = e[i].v) {
		if (vis[i >> 1]) continue; vis[i >> 1] = true;
		if (!dfn[v]) Tarjan(v), low[u] = std::min(low[u], low[v]);
		else low[u] = std::min(low[u], dfn[v]);
	}
	if (low[u] == dfn[u]) { ++scc;
		while (stk[top--] != u);
	}
}

int main() {
#ifndef DEBUG
	freopen("beehive.in", "r", stdin);
	freopen("beehive.out","w",stdout);
#endif
	scanf("%d%d", & n, & m); int u, v;
	lep(i, 1, m) scanf("%d%d", & u, & v), Add(u, v), Add(v, u);
	Tarjan(1);
	printf("%d\n", n - scc + 1);
	return 0;
}