数据结构 - 吉司机线段树

概述

吉司机线段树 (Segment Tree Beats) 指的是利用势函数分析保证复杂度来维护一些普通线段树难以维护的操作。
一般为区间历史最值。

双半群模型

半群，指定义在集合 \(S\) 上的一个运算 \(\times\) 满足结合律。
双半群，简单来说就是我们需要维护两个类 \(Info\) 和 \(Tag\) ，满足：

\((info_1 + info_2) + info_3 = info_1 + (info_2 + info_3)\)
\((tag_1 + tag_2) + tag_3 = tag_1 + (tag_2 + tag_3)\)
\((info_1 + info_2)\times tag = info_1 \times tag + info_2 \times tag\)

然后我们就可以很方便地维护各种信息。
引用 \(ydy\) \(dalao\) 的话：让线段树的难点不是线段树，而是信息的合并与维护。

操作举例

区间取 MIN / MAX

以取 \(min\) 为例。
Info : 最大值 \(mx\) , 最大值个数 \(mxc\) ，严格次大值 \(se\) ，区间和 \(sum\) 。
Tag : 最大值懒标记 \(amx\) ,非最大值懒标记 \(add\) 。
对于当前处理区间以及操作参数 \(v\) ，如果

\(mx \le v\) 。无影响，直接结束。
\(se < v <mx\) 。只会影响最大值，可以直接给最大值打懒标记。
\(v\le se\) 。递归。

时间复杂度 \(O(n\log n)\) 。
证明：考虑每次 \(3\) 操作会导致多出 \(O(1)\) 次的 \(1\)、\(2\) 操作，所以我们只分析 \(3\) 操作的复杂度。
定义势函数 \(\Phi (p)\) 表示节点 \(p\) 维护区间内的颜色种类数。
对于线段树上的每个节点，每次 \(3\) 操作递归一定会导致 \(\Phi\) 减少至少 \(1\) ，
而所有节点的 \(\Phi\) 总和是 \(O(n\log n)\) 的，所以复杂度均摊是 \(O(n\log n)\) 的。

如果加上区间加操作呢？（详细证明还是参考吉老师的论文吧）复杂度均摊 \(O(m\log^2 n)\) ，不过，目前仍旧没有数据能将其卡到这个上界，实际运行效率更接近 \(O(m\log n)\) 。

区间历史最值

我们会给一个节点打上多个标记，而标记的走势类似于：

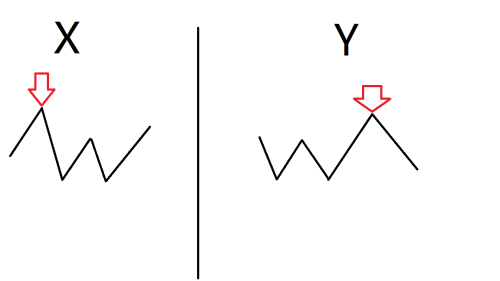
Ps: 图中 \(X\) , \(Y\) 表示两个 \(Tag\) ，而他们本身也是若干个 \(Tag\) 根据结合律合并的。

所以我们需要维护历史最大懒标记，合并时如下图：

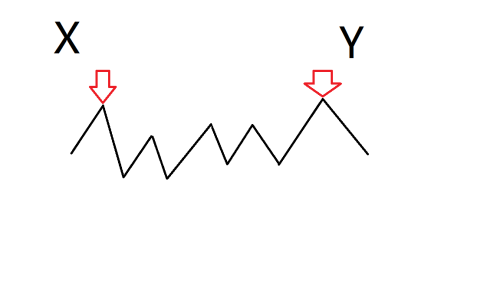
我们需要首尾相接地合并。

Info : 最大值 \(mx\) ，历史最大值 \(hmx\) 。
Tag : 懒标记 \(add\) ，历史最大懒标记 \(ha\) 。

同时我们发现， \(Info\) 与 \(Tag\) 合并依旧可以使用上面的图来理解。

历史版本和

简单的来说，维护一个 \(Tag\) 的标记表示将 \(ans\) 累加上若干倍的某个属性。

以维护 01 序列区间和的历史版本和与区间翻转为例。
Info : 历史版本和 \(ans\) ，当前区间和 \(sum\) ，区间长度 \(len\) 。
Tag : 累加 \(tc\) 倍的 \(sum\) 到 \(ans\) 里，累加 \(td\) 倍的 \(len - sum\) 到 \(ans\) 里，然后是否翻转 \(tag\)。

注意这里的 \(Tag\) 是有时间含义的。
合并 \(Tag\) \(X\) 和 \(Y\) 时，根据 \(X.tag\) 来分讨 \(Y\) 的贡献。


friend Tag operator + (const Tag& x, const Tag& y) { 
	return x.tag ? Tag(y.tag ^ 1, x.tc + y.td, x.td + y.tc) : Tag(y.tag, x.tc + y.tc, x.td + y.td); 
}

例题

P9990 [Ynoi Easy Round 2023] TEST_90

容易发现历史版本和的题目都和所有子区间这个关键词有关。
维护向右的扫描线，对于当前右端点，每个左端点有一个 \(0/1\) 状态，表示奇偶性。
加入一个新端点 \(R\)，就将其上次出现位置 \(+1\) 到当前位置的状态翻转，然后对 \([1, R]\) 累加一个版本的和。

点击查看


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 1e6 + 7;
typedef long long ll;

struct node { int l, r, id; }q[_];
struct Info {
	ll ans; int cnt, l, r;
	Info(ll _ans = 0, int _cnt = 0, int _l = 0, int _r = 0) { ans = _ans, cnt = _cnt, l = _l, r = _r; }
	friend Info operator + (const Info& x, const Info& y) { return Info(x.ans + y.ans, x.cnt + y.cnt, x.l, y.r) ; }
}tr[_ << 2];
struct Tag {
	int tag, tc, td;
	Tag(int _tag = 0, int _tc = 0, int _td = 0) { tag = _tag, tc = _tc, td = _td; }
	friend Tag operator + (const Tag& x, const Tag& y) { 
		return x.tag ? Tag(y.tag ^ 1, x.tc + y.td, x.td + y.tc) : Tag(y.tag, x.tc + y.tc, x.td + y.td); 
	}
	bool NE() { return tag or tc or td; }
}tag[_ << 2], nw;
Info operator * (const Info& x, const Tag& y) { 
	return Info( x.ans + 1ll * x.cnt * y.tc + 1ll * (x.r - x.l + 1 - x.cnt) * y.td, 
			y.tag ? (x.r - x.l + 1 - x.cnt) : x.cnt, x.l, x.r);
} 
int n, m, a[_], pre[_]; ll ans[_];

#define ls p << 1
#define rs p << 1 | 1
void PushUp(int p) { tr[p] = tr[ls] + tr[rs]; }
void UpdVal(int p, const Tag& k) { tr[p] = tr[p] * k, tag[p] = tag[p] + k; }
void PushDown(int p) { if (tag[p].NE()) UpdVal(ls, tag[p]), UpdVal(rs, tag[p]), tag[p] = Tag(); }
void Build(int l, int r, int p = 1) {
	tr[p].l = l, tr[p].r = r;
	if (l == r) return; int mid = (l + r) >> 1;
	Build(l, mid, ls), Build(mid + 1, r, rs);
}
void Modify(int l, int r, const Tag& k, int p = 1) {
	if (r < tr[p].l or tr[p].r < l) return;
	if (l <= tr[p].l and tr[p].r <= r) return UpdVal(p, k); PushDown(p);
	Modify(l, r, k, ls), Modify(l, r, k, rs); PushUp(p);
}
Info Query(int l, int r, int p = 1) {
	if (l <= tr[p].l and tr[p].r <= r) return tr[p]; PushDown(p);
	if (r <= tr[ls].r) return Query(l, r, ls); if (tr[rs].l <= l) return Query(l, r, rs);
	return Query(l, r, ls) + Query(l, r, rs);
}
#undef ls
#undef rs

int main() {
	scanf("%d", & n); Build(1, n);
	lep(i, 1, n) scanf("%d", a + i);
	scanf("%d", & m); int l, r;
	lep(i, 1, m) scanf("%d%d", & l, & r), q[i] = { l, r, i };
	std::sort(q + 1, q + 1 + m, [](const node& x, const node& y) { return x.r < y.r; });

	int R = 1;
	lep(i, 1, m) {
		while (R <= q[i].r) Modify(pre[a[R]] + 1, R, nw = Tag(1, 0, 0)), 
			Modify(1, R, nw = Tag(0, 1, 0)), pre[a[R]] = R, ++R;
		ans[q[i].id] = Query(q[i].l, q[i].r).ans;
	}
	lep(i, 1, m) printf("%lld\n", ans[i]);
	return 0;
}

P6242 【模板】线段树 3（区间最值操作、区间历史最值）

只列出关键信息。
Info : 最大值 \(mx\)，严格次大值 \(se\) ，最大值个数 \(mxc\) ，历史最大值 \(hmx\), 区间和 \(sum\)
Tag : 最大值懒标记 \(amx\) ,最大值懒标记历史最大值 \(hamx\) ，非最大值懒标记 \(add\) ，非最大值历史最大懒标记 \(ha\)。

特殊的地方是下次，要根据最大值的来源分讨。
比如说如果最大值来自左区间，左区间会下传完整标记，如果不是，则只会继承到非最大值的相关标记。

点击查看


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 1e6 + 7;
typedef long long ll;
const ll inf = 1e15;

struct Info {
	ll sum, mxc, mx, se, hmx; int l, r;
	Info(ll _sum = 0, ll _mx = 0, ll _se = -inf, ll _mxc = 0, ll _hmx = 0, int _l = 0, int _r = 0) { 
		sum = _sum, mx = _mx, se = _se, mxc = _mxc, hmx = _hmx, l = _l, r = _r;
	}
	friend Info operator + (const Info& x, const Info& y) {
		if (x.mx > y.mx) return Info(x.sum + y.sum, x.mx, std::max(x.se, y.mx), x.mxc, std::max(x.hmx, y.hmx), x.l, y.r);
		if (x.mx < y.mx) return Info(x.sum + y.sum, y.mx, std::max(y.se, x.mx), y.mxc, std::max(x.hmx, y.hmx), x.l, y.r);
		return Info(x.sum + y.sum, x.mx, std::max(x.se, y.se), x.mxc + y.mxc, std::max(x.hmx, y.hmx), x.l, y.r);
	}
}tr[_ << 2];
struct Tag {
	ll add, amx, ha, hamx;
	Tag(ll _add = 0, ll _amx = 0, ll _ha = 0, ll _hamx = 0) { add = _add, amx = _amx, ha = _ha, hamx = _hamx; }
	friend Tag operator + (const Tag& x, const Tag& y) { return Tag(x.add + y.add, x.amx + y.amx, std::max(x.ha, x.add + y.ha), std::max(x.hamx, x.amx + y.hamx)); }
	bool NE() { return add or amx or ha or hamx ; }
	Tag emx() { return Tag(add, add, ha, ha); }
}tag[_ << 2];
Info operator * (const Info& x, const Tag& y) { 
	return Info(x.sum + x.mxc * y.amx + (x.r - x.l + 1 - x.mxc) * y.add, 
			x.mx + y.amx, x.se == -inf ? -inf : x.se + y.add, x.mxc, std::max(x.hmx, x.mx + y.hamx), x.l, x.r);
} 
int n, m, a[_];

#define ls p << 1
#define rs p << 1 | 1
void PushUp(int p) { tr[p] = tr[ls] + tr[rs]; }
void UpdVal(int p, const Tag& k) { tr[p] = tr[p] * k, tag[p] = tag[p] + k; }
void PushDown(int p) { 
	if (tag[p].NE()) {
		ll l = tr[ls].mx, r = tr[rs].mx;
		if (l >= r) UpdVal(ls, tag[p]);
		else UpdVal(ls, tag[p].emx());
		if (r >= l) UpdVal(rs, tag[p]);
		else UpdVal(rs, tag[p].emx());
		tag[p] = Tag();
	}
}
void Build(int l, int r, int p = 1) {
	if (l == r) { tr[p] = { a[l], a[l], -inf, 1, a[l], l, l }; return ; } int mid = (l + r) >> 1;
	Build(l, mid, ls), Build(mid + 1, r, rs); PushUp(p);
}
void Modify(int l, int r, int k, int p = 1) {
	if (r < tr[p].l or tr[p].r < l) return;
	if (l <= tr[p].l and tr[p].r <= r) {
		if (tr[p].mx <= k) return;
		if (tr[p].se < k) return UpdVal(p, Tag(0, k - tr[p].mx, 0, k - tr[p].mx));
	} PushDown(p);
	Modify(l, r, k, ls), Modify(l, r, k, rs); PushUp(p);
}
void Modify(int l, int r, const Tag& k, int p = 1) {
	if (r < tr[p].l or tr[p].r < l) return;
	if (l <= tr[p].l and tr[p].r <= r) return UpdVal(p, k); PushDown(p);
	Modify(l, r, k, ls), Modify(l, r, k, rs); PushUp(p);
}
Info Query(int l, int r, int p = 1) {
	if (l <= tr[p].l and tr[p].r <= r) return tr[p]; PushDown(p);
	if (r <= tr[ls].r) return Query(l, r, ls); if (tr[rs].l <= l) return Query(l, r, rs);
	return Query(l, r, ls) + Query(l, r, rs);
}
#undef ls
#undef rs

int main() {
	scanf("%d%d", & n, & m);
	lep(i, 1, n) scanf("%d", a + i); Build(1, n);

	int op, l, r, k;
	while (m--) {
		scanf("%d%d%d", & op, & l, & r);
		if (op == 1) scanf("%d", & k), Modify(l, r, Tag(k, k, k, k));
		else if (op == 2) scanf("%d", & k), Modify(l, r, k);
		else if (op == 3) printf("%lld\n", Query(l, r).sum);
		else if (op == 4) printf("%lld\n", Query(l, r).mx);
		else printf("%lld\n", Query(l, r).hmx);
	}
	return 0;
}

P10639 BZOJ4695 最佳女选手

发现维护的时候要分讨区间种类数，所以我们稍稍修改 \(Tag\) 的含义。

Tag : 最大值懒标记 \(amx\) ，最小值懒标记 \(mn\) ，所有值懒标记 \(add\) 。

这样在区间加时就可以只修改 \(add\) 标记，维护细节会少很多。

点击查看


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 1e6 + 7;
typedef long long ll;
const ll inf = 1e15;

struct Info {
	ll sum, mxc, mnc, mx, se, mn, th; int l, r;
	Info(ll _sum = 0, ll _mx = 0, ll _se = -inf, ll _mxc = 0, ll _mn = 0, ll _th = inf, ll _mnc = 0, int _l = 0, int _r = 0) { 
		sum = _sum, mx = _mx, se = _se, mxc = _mxc, mn = _mn, th = _th, mnc = _mnc, l = _l, r = _r;
	}
	friend Info operator + (const Info& x, const Info& y) {
		ll mx = 0, se = -inf, mxc = 0, mn = 0, th = inf, mnc = 0;
		if (x.mx > y.mx) mx = x.mx, se = std::max(x.se, y.mx), mxc = x.mxc;
		else if (x.mx < y.mx) mx = y.mx, se = std::max(y.se, x.mx), mxc = y.mxc;
		else mx = x.mx, se = std::max(x.se, y.se), mxc = x.mxc + y.mxc;
		if (x.mn < y.mn) mn = x.mn, th = std::min(x.th, y.mn), mnc = x.mnc;
		else if (x.mn > y.mn) mn = y.mn, th = std::min(y.th, x.mn), mnc = y.mnc;
		else mn = x.mn, th = std::min(x.th, y.th), mnc = x.mnc + y.mnc;
		return Info(x.sum + y.sum, mx, se, mxc, mn, th, mnc, x.l, y.r);
	}
}tr[_ << 2];
struct Tag {
	ll add, amx, amn;
	Tag(ll _add = 0, ll _amx = 0, ll _amn = 0) { add = _add, amx = _amx, amn = _amn; }
	friend Tag operator + (const Tag& x, const Tag& y) { return Tag(x.add + y.add, x.amx + y.amx, x.amn + y.amn); }
	bool NE() { return add or amx or amn ; }
}tag[_ << 2];
Info operator * (const Info& x, const Tag& y) { 
	if (x.mx == x.mn) return Info(x.sum + (x.r - x.l + 1) * (y.add + y.amx + y.amn), x.mx + y.add + y.amx + y.amn, 
			x.se, x.mxc, x.mn + y.add + y.amx + y.amn, x.th, x.mnc, x.l, x.r);
	if (x.mn == x.se) return Info(x.sum + x.mxc * (y.amx + y.add) + x.mnc * (y.amn + y.add), 
			x.mx + y.add + y.amx, x.se + y.add + y.amn, x.mxc, x.mn + y.add + y.amn, x.th + y.add + y.amx, x.mnc, x.l, x.r);
	return Info(x.sum + x.mxc * y.amx + x.mnc * y.amn + (x.r - x.l + 1) * y.add, 
			x.mx + y.add + y.amx, x.se + y.add, x.mxc, x.mn + y.add + y.amn, x.th + y.add, x.mnc, x.l, x.r);
} 
int n, m, a[_];

#define ls p << 1
#define rs p << 1 | 1
void PushUp(int p) { tr[p] = tr[ls] + tr[rs]; }
void UpdVal(int p, const Tag& k) { tr[p] = tr[p] * k, tag[p] = tag[p] + k; }
void PushDown(int p) { 
	if (tag[p].NE()) {
		ll lx = tr[ls].mx, rx = tr[rs].mx;
		ll ln = tr[ls].mn, rn = tr[rs].mn;
		UpdVal(ls, Tag(tag[p].add, (lx >= rx) * tag[p].amx, (ln <= rn) * tag[p].amn)), 
		UpdVal(rs, Tag(tag[p].add, (rx >= lx) * tag[p].amx, (rn <= ln) * tag[p].amn));
		tag[p] = Tag();
	}
}
void Build(int l, int r, int p = 1) {
	if (l == r) { tr[p] = { a[l], a[l], -inf, 1, a[l], inf, 1, l, l }; return ; } int mid = (l + r) >> 1;
	Build(l, mid, ls), Build(mid + 1, r, rs); PushUp(p);
}
void MIN(int l, int r, int k, int p = 1) {
	if (r < tr[p].l or tr[p].r < l) return;
	if (l <= tr[p].l and tr[p].r <= r) {
		if (tr[p].mx <= k) return;
		if (tr[p].se < k) return UpdVal(p, Tag(0, k - tr[p].mx));
	} PushDown(p);
	MIN(l, r, k, ls), MIN(l, r, k, rs); PushUp(p);
}
void MAX(int l, int r, int k, int p = 1) {
	if (r < tr[p].l or tr[p].r < l) return;
	if (l <= tr[p].l and tr[p].r <= r) {
		if (tr[p].mn >= k) return;
		if (tr[p].th > k) return UpdVal(p, Tag(0, 0, k - tr[p].mn));
	} PushDown(p);
	MAX(l, r, k, ls), MAX(l, r, k, rs); PushUp(p);
}
void Modify(int l, int r, int k, int p = 1) {
	if (r < tr[p].l or tr[p].r < l) return;
	if (l <= tr[p].l and tr[p].r <= r) return UpdVal(p, Tag(k));
	PushDown(p);
	Modify(l, r, k, ls), Modify(l, r, k, rs); PushUp(p);
}
Info Query(int l, int r, int p = 1) {
	if (l <= tr[p].l and tr[p].r <= r) return tr[p]; PushDown(p);
	if (r <= tr[ls].r) return Query(l, r, ls); if (tr[rs].l <= l) return Query(l, r, rs);
	return Query(l, r, ls) + Query(l, r, rs);
}
#undef ls
#undef rs

int main() {
	scanf("%d", & n);
	lep(i, 1, n) scanf("%d", a + i); Build(1, n);

	scanf("%d", & m);
	int op, l, r, k;
	while (m--) {
		scanf("%d%d%d", & op, & l, & r);
		if (op == 1) scanf("%d", & k), Modify(l, r, k);
		else if (op == 2) scanf("%d", & k), MAX(l, r, k);
		else if (op == 3) scanf("%d", & k), MIN(l, r, k);
		else if (op == 4) printf("%lld\n", Query(l, r).sum);
		else if (op == 5) printf("%lld\n", Query(l, r).mx);
		else printf("%lld\n", Query(l, r).mn);
	}
	return 0;
}

P4314 CPU 监控

Tag : 覆盖 \(col\) ，历史最大值 \(hmx\) ，加法懒标记 \(add\) ，历史最大懒标记 \(ha\) 。
同样按照 \(col\) 分讨，注意 \(ha\) 只能维护在区间推平之前的标记，推平之后的最大值使用 \(hmx\) 记录。
\(Info \times Tag\) 时注意考虑 \(Tag\) 合并中出现过的最大值。

点击查看


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 1e6 + 7;
const int inf = 2e9;
typedef long long ll;

struct Info {
	int mx, hmx; int l, r;
	Info(int _mx = 0, int _hmx = 0, int _l = 0, int _r = 0) { mx = _mx, hmx = _hmx, l = _l, r = _r; }
	friend Info operator + (const Info& x, const Info& y) { return Info(std::max(x.mx, y.mx), std::max(x.hmx, y.hmx), x.l, y.r); }
}tr[_ << 2];
struct Tag {
	int col, hmx, add, ha;
	Tag(int _col = inf, int _hmx = -inf, int _add = 0, int _ha = 0) { col = _col, hmx = _hmx, add = _add, ha = _ha; }
	friend Tag operator + (const Tag& x, const Tag& y) { int hmx = std::max(x.hmx, y.hmx);
		if (x.col != inf) return Tag(y.col != inf ? y.col : x.col + y.add, std::max(hmx, x.col + y.ha), 0, x.ha);
		if (y.col != inf) return Tag(y.col, hmx, 0, std::max(x.ha, x.add + y.ha));
		return Tag(inf, hmx, x.add + y.add, std::max(x.ha, x.add + y.ha));
	}
	bool NE() { return col != inf or hmx != -inf or add or ha; }
}tag[_ << 2];
Info operator * (const Info& x, const Tag& y) { return Info(y.col != inf ? y.col : x.mx + y.add, std::max(std::max(x.hmx, y.hmx), x.mx + y.ha), x.l, x.r); } 
int n, m, a[_];

#define ls p << 1
#define rs p << 1 | 1
void PushUp(int p) { tr[p] = tr[ls] + tr[rs]; }
void UpdVal(int p, const Tag& k) { tr[p] = tr[p] * k, tag[p] = tag[p] + k; }
void PushDown(int p) { if (tag[p].NE()) UpdVal(ls, tag[p]), UpdVal(rs, tag[p]), tag[p] = Tag(); }
void Build(int l, int r, int p = 1) {
	if (l == r) { tr[p] = { a[l], a[l], l, l }; return ; } int mid = (l + r) >> 1;
	Build(l, mid, ls), Build(mid + 1, r, rs); PushUp(p);
}
void Modify(int l, int r, const Tag& k, int p = 1) {
	if (r < tr[p].l or tr[p].r < l) return;
	if (l <= tr[p].l and tr[p].r <= r) return UpdVal(p, k); PushDown(p);
	Modify(l, r, k, ls), Modify(l, r, k, rs); PushUp(p);
}
Info Query(int l, int r, int p = 1) {
	if (l <= tr[p].l and tr[p].r <= r) return tr[p]; PushDown(p);
	if (r <= tr[ls].r) return Query(l, r, ls); if (tr[rs].l <= l) return Query(l, r, rs);
	return Query(l, r, ls) + Query(l, r, rs);
}
#undef ls
#undef rs

int main() {
	scanf("%d", & n);
	lep(i, 1, n) scanf("%d", a + i); Build(1, n);

	scanf("%d", & m);
	int l, r, k; char op;
	while (m--) {
		scanf(" %c%d%d", & op, & l, & r);
		if (op == 'P') scanf("%d", & k), Modify(l, r, Tag(inf, -inf, k, k));
		else if (op == 'C') scanf("%d", & k), Modify(l, r, Tag(k, k));
		else if (op == 'Q') printf("%d\n", Query(l, r).mx);
		else printf("%d\n", Query(l, r).hmx);
	}
	return 0;
}

posted @ 2025-07-08 09:48 qkhm 阅读(59) 评论(0) 收藏举报

刷新页面返回顶部

Loading

幽光闪烁

数据结构 - 吉司机线段树

概述

双半群模型

操作举例

区间取 MIN / MAX

区间历史最值

历史版本和

例题

P9990 [Ynoi Easy Round 2023] TEST_90

P6242 【模板】线段树 3（区间最值操作、区间历史最值）

P10639 BZOJ4695 最佳女选手

P4314 CPU 监控

公告