2025.7.5 测试
AT_abc342_g [ABC342G] Retroactive Range Chmax
线段树套 set,使用标记永久化维护即可。
点击查看
#include <bits/stdc++.h>
#define DEBUG
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 2e5 + 7;
typedef long long ll;
int n, m, a[_], l[_], r[_], x[_];
std::multiset <int> tr[_ << 2];
#define ls p << 1
#define rs p << 1 | 1
void Build(int l, int r, int p) {
if (l == r) { tr[p].insert(a[l]); return; } int mid = (l + r) >> 1;
Build(l, mid, ls), Build(mid + 1, r, rs);
}
void Modify(int l, int r, int s, int t, int x, int p) {
if (r < s or t < l) return;
if (l <= s and t <= r) { tr[p].insert(x); return; } int mid = s + t >> 1;
Modify(l, r, s, mid, x, ls), Modify(l, r, mid + 1, t, x, rs);
}
void Erase(int l, int r, int s, int t, int x, int p) {
if (r < s or t < l) return;
if (l <= s and t <= r) { tr[p].erase(tr[p].find(x)); return; } int mid = s + t >> 1;
Erase(l, r, s, mid, x, ls), Erase(l, r, mid + 1, t, x, rs);
}
int Query(int d, int s, int t, int p) {
int res = 0;
if (!tr[p].empty()) res = *tr[p].rbegin();
if (s == t) return res; int mid = s + t >> 1;
return std::max(res, d <= mid ? Query(d, s, mid, ls) : Query(d, mid + 1, t, rs));
}
#undef ls
#undef rs
int main() {
#ifndef DEBUG
freopen("war.in", "r", stdin);
freopen("war.out","w",stdout);
#endif
scanf("%d", & n);
lep(i, 1, n) scanf("%d", a + i); int op;
Build(1, n, 1);
scanf("%d", & m);
lep(i, 1, m) {
scanf("%d", & op);
if (op == 1) scanf("%d%d%d", l + i, r + i, x + i), Modify(l[i], r[i], 1, n, x[i], 1);
else if (op == 2) scanf("%d", x + i), Erase(l[x[i]], r[x[i]], 1, n, x[x[i]], 1);
else scanf("%d", x + i), printf("%d\n", Query(x[i], 1, n, 1));
}
return 0;
}
CF293B Distinct Paths
注意到 \(n + m - 1 > k\) 时方案数为 \(0\) ,数据范围很小,直接搜索。
剪枝考虑两点:
- 如果剩下的颜色不够用了,直接结束。
- 从未出现过的颜色是本质相同的,可以直接复用返回值
点击查看
#include <bits/stdc++.h>
#define DEBUG
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 11;
const int mod = 1e9 + 7;
typedef long long ll;
int n, m, k, a[_][_], ans, col[_], sum[_];
int Dfs(int x, int y, int S) {
if (y == m + 1) return Dfs(x + 1, 1, 0);
if (x == n + 1) return 1;
if (k - __builtin_popcount(S | col[y]) < (n - x + 1) + (m - y)) return 0;
if (a[x][y]) {
if ((S >> a[x][y] - 1) & 1) return 0;
if ((col[y] >> a[x][y] - 1) & 1) return 0;
col[y] |= (1 << a[x][y] - 1), ++sum[a[x][y]];
int res = Dfs(x, y + 1, S | col[y]);
col[y] ^= (1 << a[x][y] - 1), --sum[a[x][y]];
return res;
}
int res = -1, tot = 0, nw;
lep(i, 1, k) {
if (!(((S | col[y]) >> i - 1) & 1)) {
if (~res and !sum[i]) { tot = (tot + 1ll * res) % mod; continue; }
++sum[i], col[y] |= (1 << i - 1), nw = Dfs(x, y + 1, S | col[y]), col[y] ^= (1 << i - 1), --sum[i];
tot = (tot + 1ll * nw) % mod;
if (!sum[i]) res = nw;
}
}
return tot;
}
int main() {
#ifndef DEBUG
freopen("paint.in", "r", stdin);
freopen("paint.out","w",stdout);
#endif
scanf("%d%d%d", & n, & m, & k);
if (n + m - 1 > k) { puts("0"); return 0; }
lep(i, 1, n) lep(j, 1, m) scanf("%d", a[i] + j), ++sum[a[i][j]];
ans = Dfs(0, m + 1, 0);
printf("%d\n", ans);
return 0;
}
AT_arc176_e [ARC176E] Max Vector
值域较小,对每一个值域建点,用于维护至少为某值的信息。
形式如下:
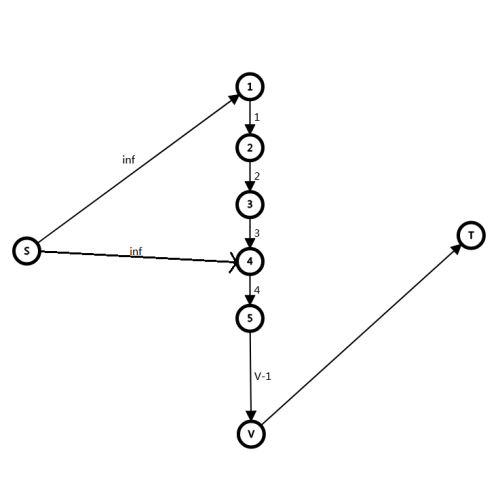
表示这个变量至少选 \(4\) 。
对于本题来说,将 \(x_i\) 和 \(y_i\) 反着建,然后每次操作就将对应的值域点与操作点相连。
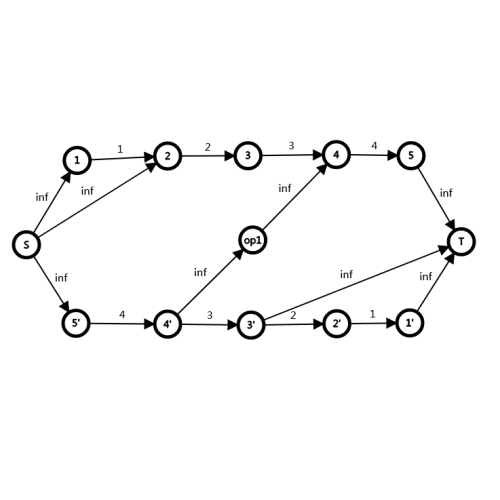
这张图就表示 \(x=2\) , \(y=3\) , \(a=4\) , \(V=4\) 。
\(op1\) 所连的边表示 \(x\) , \(y\) 其中一个需要接受 \(\ge 4\) 限制。
点击查看
#include <bits/stdc++.h>
#define DEBUG
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(G, i, u, t) for (int i = G[u], t = e[i].v; i; i = e[i].n, t = e[i].v)
const int _ = 100000 + 7;
const int V = 500;
const int inf = 1e9;
struct Edge { int v, n, c; }e[_ << 6]; int H[_], cur[_], cnte = 1;
int n, m, a[V + 1][12], x[12], y[12], S, T;
int dep[_];
void Add(int u, int v, int c) { e[++cnte] = { v, H[u], c }, H[u] = cnte, e[++cnte] = { u, H[v], 0 }, H[v] = cnte; }
int Id(int op, int x, int v) { return op * n * (V + 1) + (x - 1) * (V + 1) + v; }
void Init() { T = 2 * n * (V + 1) + m + 1;
lep(i, 1, n) {
Add(S, Id(0, i, 1), inf), Add(S, Id(1, i, V + 1), inf);
Add(Id(0, i, V + 1), T, inf), Add(Id(1, i, 1), T, inf);
Add(S, Id(0, i, x[i]), inf), Add(Id(1, i, y[i]), T, inf);
lep(j, 1, V) Add(Id(0, i, j), Id(0, i, j + 1), j), Add(Id(1, i, j + 1), Id(1, i, j), j);
}
lep(i, 1, m) {
int p = 2 * n * (V + 1) + i;
lep(j, 1, n) Add(Id(1, j, a[i][j]), p, inf), Add(p, Id(0, j, a[i][j]), inf);
}
}
bool Bfs() { std::queue <int> d;
lep(i, S, T) dep[i] = 0;
dep[S] = 1; d.push(S);
while (!d.empty()) {
int u = d.front(); d.pop();
if (u == T) return true;
ep(H, i, u, v) if (e[i].c > 0 and !dep[v]) {
dep[v] = dep[u] + 1;
d.push(v);
}
}
return false;
}
int Dfs(int u, int flow) {
if (u == T or !flow) return flow;
int tot = 0, nw;
ep(cur, i, u, v) { cur[u] = i;
if (!flow) break;
if (e[i].c == 0 or dep[v] != dep[u] + 1) continue;
nw = Dfs(v, std::min(e[i].c, flow));
if (!nw) { dep[v] = 0; continue; }
e[i].c -= nw, e[i ^ 1].c += nw, tot += nw, flow -= nw;
}
return tot;
}
int Dinic() { int flow = 0;
while (Bfs()) {
lep(i, S, T) cur[i] = H[i];
flow += Dfs(S, inf);
}
return flow;
}
int main() {
#ifndef DEBUG
freopen("game.in", "r", stdin);
freopen("game.out","w",stdout);
#endif
scanf("%d%d", & n, & m);
lep(i, 1, n) scanf("%d", x + i);
lep(i, 1, n) scanf("%d", y + i);
lep(i, 1, m) lep(j, 1, n) scanf("%d", a[i] + j);
Init();
printf("%d\n", Dinic());
return 0;
}
AT_arc180_d [ARC180D] Division into 3
考虑区间最大值的被划为在了左侧 \(or\) 中间 \(or\) 右侧 。
中间的话,贡献加上两个端点,调整法证明即可。
左侧 \(or\) 右侧是类似的,这里以左侧为例。
可以发现,中间的一段一定只有一个元素,因为如果不止一个元素,将除了最右侧的所有元素划分给最大值一定不劣。
所以一个位置 \(i\) 的贡献就变成了 \(a_i + sufmax_{i + 1}\) ,见到后缀最大值,考虑扫描线 + 单调栈。
具体的,将询问按照右端点升序处理,以此将合法的位置加入单调栈,同时用线段树维护最小值。
如果新加入的元素比栈顶大,则清除掉栈顶的贡献,最后加入本身的贡献。
栈内每个元素 \(stk_i\) 的贡献形如,将 \(stk_{i-1}\sim stk_i - 1\) 的位置权值加上 \(a_{stk_i}\) 。
点击查看
#include <bits/stdc++.h>
#define DEBUG
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 3e5 + 7;
typedef long long ll;
const ll inf = 1e15;
struct node { int l, r, id; }q[_], p[_];
int n, m, st[_][21], lg[_]; ll ans[_], a[_];
int stk[_], top;
int tag[_ << 2], ls[_ << 2], rs[_ << 2], rt, tot; ll mn[_ << 2];
int Upd(int x, int y) { return a[x] > a[y] ? x : y; }
void Init() {
lep(i, 2, n) lg[i] = lg[i >> 1] + 1;
lep(j, 1, 20) lep(i, 1, n - (1 << j) + 1)
st[i][j] = Upd(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
}
int MAX(int l, int r) { int k = lg[r - l + 1]; return Upd(st[l][k], st[r - (1 << k) + 1][k]); }
int New() { int p = ++tot; ls[p] = rs[p] = tag[p] = 0, mn[p] = inf; return p; }
void PushUp(int p) { mn[p] = std::min(mn[ls[p]], mn[rs[p]]); }
void UpdVal(int p, ll k) { mn[p] += k, tag[p] += k; }
void PushDown(int p) { if (tag[p]) UpdVal(ls[p], tag[p]), UpdVal(rs[p], tag[p]), tag[p] = 0; }
void Build(int l, int r, int& p) {
p = New();
if (l == r) { mn[p] = a[l]; return; } int mid = (l + r) >> 1;
Build(l, mid, ls[p]), Build(mid + 1, r, rs[p]); PushUp(p);
}
void Modify(int l, int r, int s, int t, int d, int p) {
if (r < s or t < l) return;
if (l <= s and t <= r) return UpdVal(p, d); int mid = (s + t) >> 1; PushDown(p);
Modify(l, r, s, mid, d, ls[p]), Modify(l, r, mid + 1, t, d, rs[p]); PushUp(p);
}
ll Query(int l, int r, int s, int t, int p) {
if (!p or r < s or t < l or l > r) return inf;
if (l <= s and t <= r) return mn[p]; int mid = (s + t) >> 1; PushDown(p);
return std::min(Query(l, r, s, mid, ls[p]), Query(l, r, mid + 1, t, rs[p]));
}
void AddR(int p) {
while (top and a[stk[top]] < a[p]) Modify(stk[top - 1], stk[top] - 1, 1, n, -a[stk[top]], rt), --top;
Modify(stk[top], p - 1, 1, n, a[p], rt), stk[++top] = p;
}
void AddL(int p) {
while (top and a[stk[top]] < a[p]) Modify(stk[top] + 1, stk[top - 1], 1, n, -a[stk[top]], rt), --top;
Modify(p + 1, stk[top], 1, n, a[p], rt), stk[++top] = p;
}
int main() {
#ifndef DEBUG
freopen("division.in", "r", stdin);
freopen("division.out","w",stdout);
#endif
scanf("%d%d", & n, & m);
lep(i, 1, n) scanf("%lld", a + i), st[i][0] = i; int l, r;
Init();
lep(i, 1, m) { scanf("%d%d", & l, & r); ans[i] = inf;
int pos = MAX(l, r);
if (l < pos and pos < r) ans[i] = std::min(ans[i], a[l] + a[pos] + a[r]);
q[i] = { l, pos, i }, p[i] = { pos, r, i };
}
std::sort(p + 1, p + 1 + m, [](const node& x, const node& y) { return x.r < y.r; });
int R = 0; stk[0] = 1; Build(1, n, rt);
lep(i, 1, m) {
while (R < p[i].r) AddR(++R);
if (p[i].l + 1 < p[i].r) ans[p[i].id] = std::min(ans[p[i].id], a[p[i].l] + Query(p[i].l + 1, p[i].r - 1, 1, n, rt));
} rt = tot = top = 0; stk[0] = n; Build(1, n, rt);
int L = n + 1;
std::sort(q + 1, q + 1 + m, [](const node& x, const node& y) { return x.l > y.l; });
lep(i, 1, m) {
while (L > q[i].l) AddL(--L);
if (q[i].l + 1 < q[i].r) ans[q[i].id] = std::min(ans[q[i].id], a[q[i].r] + Query(q[i].l + 1, q[i].r - 1, 1, n, rt));
}
lep(i, 1, m) printf("%lld\n", ans[i]);
return 0;
}
时间仓促,如有错误欢迎指出,欢迎在评论区讨论,如对您有帮助还请点个推荐、关注支持一下

 树套树+剪纸+最小割+扫描线/单调栈
树套树+剪纸+最小割+扫描线/单调栈

 浙公网安备 33010602011771号
浙公网安备 33010602011771号