那快把题端上来吧 （二）

CF848C Goodbye Souvenir

\(\boldsymbol{CDQ}\) 。

\(CDQ\) 只能维护每个区间贡献独立的操作，考虑将所有修改造成的贡献离线下来。
具体的，用 set 维护每种颜色出现的位置，每次插入删除都会生成若干个形如 \((l, r, t)\) 的三元组。
维护三元组的偏序关系即可。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 2e6 + 7;
typedef long long ll;

struct node { int t, pos, pre, op; }q[_]; int tot;
int n, m, a[_], Q; ll ans[_], c[_];
std::set <int> S[_];

void Add(int x, int k) { while (x <= n) c[x] += k, x += x & -x; }
ll Query(int x) { ll res = 0; while (x) res += c[x], x -= x & -x; return res; }
void Ins(int t, int c, int x) {
	S[c].insert(x);
	auto pos = S[c].find(x), fir = pos, sec = pos;
	if (pos != S[c].begin()) --fir, q[++tot] = { t, x, *fir, 0 };
	++sec; if (sec != S[c].end()) q[++tot] = { t, *sec, x, 0 };
	if (pos != S[c].begin() and sec != S[c].end()) q[++tot] = { t, *sec, *fir, -1 };
}
void Del(int t, int c, int x) {
	auto pos = S[c].find(x), fir = pos, sec = pos;
	if (pos != S[c].begin()) { --fir;
		q[++tot] = { t, x, *fir, -1 }; ++sec; 
		if (sec != S[c].end()) q[++tot] = { t, *sec, x, -1 }, q[++tot] = { t, *sec, *fir, 0 };
	}
	else { ++sec; if (sec != S[c].end()) q[++tot] = { t, *sec, x, -1 }; }
	S[c].erase(pos);
}
void CDQ(int l, int r) {
	if (l == r) return; int mid = (l + r) >> 1;
	CDQ(l, mid), CDQ(mid + 1, r); auto cmp = [](const node& x, const node& y) { return x.pos < y.pos; };
	std::sort(q + l, q + mid + 1, cmp), std::sort(q + mid + 1, q + r + 1, cmp);
	int R = l;
	lep(i, mid + 1, r) {
		while (R <= mid and q[R].pos <= q[i].pos) {
			if (q[R].op == 0) Add(n - q[R].pre + 1, q[R].pos - q[R].pre);
			else if (q[R].op == -1) Add(n - q[R].pre + 1, q[R].pre - q[R].pos);
			++R;
		}
		if (q[i].op > 0) ans[q[i].op] += Query(n - q[i].pre + 1);
	}
	lep(i, l, R - 1) {
		if (q[i].op == 0) Add(n - q[i].pre + 1, q[i].pre - q[i].pos);
		else if (q[i].op == -1) Add(n - q[i].pre + 1, q[i].pos - q[i].pre);
	}
}

int main() {
	scanf("%d%d", & n, & m);
	lep(i, 1, n) scanf("%d", a + i), Ins(0, a[i], i); int op, x, y;
	lep(i, 1, m) {
		scanf("%d%d%d", & op, & x, & y); 
		if (op == 1) Del(i, a[x], x), Ins(i, a[x] = y, x);
		else q[++tot] = { i, y, x, ++Q };
	}
	std::sort(q + 1, q + 1 + tot, [](const node& x, const node& y) { return x.t != y.t ? x.t < y.t : x.op < y.op; });
	CDQ(1, tot);
	lep(i, 1, Q) printf("%lld\n", ans[i]);
	return 0;
}

P4027 [NOI2007] 货币兑换

\(\boldsymbol{CDQ 实现斜率优化}\) 。

先复习一下斜率优化，当我们拥有一个 \(O(n^2)\) 的转移形如：
\(b(i) = \min\{-k(i)*x(j) + y(j)\}\) 时，发现其满足一次函数 \(y = kx + b\) 的形式。
将每一个 \(j\) 看做一个点 \((x(j), y(j))\) ，转移时看做一条斜率为 \(k(i)\) 的直线与某个点相交后的截距最小。
找最小截距的过程可以看做这条直线一直向上移动，直到与某个点相交，如图：

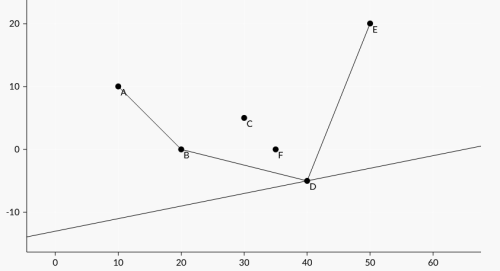
容易发现它一定会切在所有点的下凸壳上，维护下凸壳后可二分快速转移。
当所有 \(x(j)\) 单调时，我们可以快速维护下凸壳，但当 \(x(j)\) 不单调时，我们就需要使用 \(CDQ\) 或者 李超树解决。
下面介绍 \(CDQ\) 写法。
发现维护下凸壳满足我们所说的贡献独立的原则，使用 \(CDQ\) 优化。
具体的，对于当前维护的区间，先递归处理左侧的 \(dp\) 值，再把左侧区间的下凸壳维护处理，更新右侧区间的 \(dp\) 值。
这样，每个位置都被左侧更新完后才会更新右侧。

附一张 \(CDQ\) 转移图：

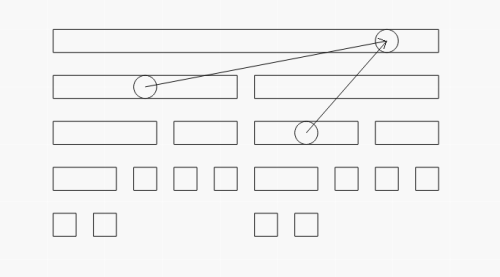
对于这题，可以推出 \(DP\) 转移：

\[f_i = \frac{f_jr_j}{r_ja_j+b_j} a_i + \frac{f_j}{r_ja_j+b_j}b_i \]

，发现并不满足 \(b(i)=-k(i)x(j)+y(j)\) 的一般形式。
但是可以同除 \(b_i\) ，得到：

\[\frac{f_i}{b_i} = \frac{f_jr_j}{r_ja_j+b_j} \frac{a_i}{b_i} + \frac{f_j}{r_ja_j+b_j} \]

，就满足了， \(CDQ\) 维护即可。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 1e5 + 7;
typedef double D;
typedef std::pair<D, D> PDD;

int n, id[_]; D dp[_], a[_], b[_], r[_], ans;
int stk[_], top;

D X(int x) { return (-dp[x] * r[x]) / (a[x] * r[x] + b[x]); }
D Y(int x) { return dp[x] / (a[x] * r[x] + b[x]); }
PDD Vec(int x, int y) { return { X(y) - X(x), Y(y) - Y(x) }; }
D Xor(PDD x, PDD y) { return x.first * y.second - y.first * x.second; }
bool Check(int x, int y, D k) { return Y(y) - Y(x) <= k * (X(y) - X(x)); }
void CDQ(int l, int r) {
	if (l == r) return; int mid = (l + r) >> 1;
	CDQ(l, mid); top = 0;
	std::sort(id + l, id + mid + 1, [](const int& x, const int& y) { return X(x) != X(y) ? X(x) < X(y) : Y(x) > Y(y); });
	lep(j, l, mid) { int i = id[j];
		while (top > 1 and Xor(Vec(stk[top - 1], stk[top]), Vec(stk[top], i)) >= 0) --top;
		stk[++top] = i;
	}
	lep(j, mid + 1, r) { int i = id[j];
		int L = 1, R = top;
		while (L < R) { int mid = (L + R) >> 1;
			if (Check(stk[mid], stk[mid + 1], a[i] / b[i])) R = mid;
			else L = mid + 1;
		}
		dp[i] = std::max(dp[i], dp[i - 1]);
		dp[i] = std::max(dp[i], -X(stk[L]) * a[i] + Y(stk[L]) * b[i]);
	}
	std::sort(id + mid + 1, id + r + 1); CDQ(mid + 1, r);
}

int main() {
	scanf("%d%lf", & n, dp + 1);
	lep(i, 1, n) scanf("%lf%lf%lf", a + i, b + i, r + i), id[i] = i;
	CDQ(1, n);
	lep(i, 1, n) ans = std::max(ans, dp[i]);
	printf("%.6lf\n", ans);
	return 0;
}

P3674 小清新人渣的本愿

\(\boldsymbol{bitset ， 莫队}\) 。

看到是否存在差为 \(x\) 的两个数，且值域很小，考虑 \(bitset\) 。
差可以直接判断，积可以 \(O(\sqrt n)\) 找因数。
下面讲讲如何处理和。
如果有两个数 \(a\), \(b\) 满足：
\(a + b = x\) ，那么，\(a = (V - b) - (V - x)\) 。
所以维护一个 \(bitset\) 表示 \(V-x\) 是否存在即可。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 1e5 + 7;
const int V = 1e5;

struct node { int op, l, r, x, id; }q[_];
int n, m, a[_], cnt[_], bel[_], B;
std::bitset<V + 1> S, T; bool ans[_];

void Add(int x) { if (!cnt[x]) S[x] = true, T[V - x] = true; ++cnt[x]; }
void Del(int x) { --cnt[x]; if (!cnt[x]) S[x] = false, T[V - x] = false; }

int main() {
	scanf("%d%d", & n, & m); B = n / std::sqrt(m);
	lep(i, 1, n) scanf("%d", a + i), bel[i] = (i - 1) / B + 1;
	int l, r, op, x;
	lep(i, 1, m) scanf("%d%d%d%d", & op, & l, & r, & x), q[i] = { op, l, r, x, i };
	std::sort(q + 1, q + 1 + m, [](const node&x, const node&y) {
			return bel[x.l] ^ bel[y.l] ? x.l < y.l : ((bel[x.l] & 1) ? x.r < y.r : x.r > y.r); });

	int L = 1, R = 0;
	lep(i, 1, m) { l = q[i].l, r = q[i].r, op = q[i].op, x = q[i].x;
		while (R < r) Add(a[++R]);
		while (l < L) Add(a[--L]);
		while (r < R) Del(a[R--]);
		while (L < l) Del(a[L++]);
		bool flag = false;
		if (op == 1) { if ((S & (S << x)).any()) flag = true; }
		else if (op == 2) { if ((S & (T >> (V - x))).any()) flag = true; }
		else {
			for (int i = 1; 1ll * i * i <= x; ++i)
				if (x % i == 0 and S[i] and S[x / i]) { flag = true; break; }
		}
		ans[q[i].id] = flag;
	}

	lep(i, 1, m) puts(ans[i] ? "hana" : "bi");
	return 0;
}

SP11470 TTM - To the moon

\(\boldsymbol{标记永久化}\) 。

明确每个点的维护信息就好了。
\(sum_p\) 表示当前区间的和， \(tag_p\) 表示当前区间的数都加上了这个值。
所以 \(PushUp(p)\) 时要考虑 \(tag\) 的贡献，就像平衡树。
sum[p] = sum[ls] + sum[rs] + (r - l + 1) * tag[p]

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 1e5 + 7;
typedef long long ll;

int n, m, a[_], rt[_], ls[_ << 5], rs[_ << 5], tot, t;
ll sum[_ << 5], tag[_ << 5];

void PushUp(int p, int s, int t) { sum[p] = sum[ls[p]] + sum[rs[p]] + tag[p] * (t - s + 1); }
void Build(int l, int r, int& p) {
	p = ++tot;
	if (l == r) { sum[p] = a[l]; return; } int mid = (l + r) >> 1;
	Build(l, mid, ls[p]), Build(mid + 1, r, rs[p]); PushUp(p, l, r);
}
void Modify(int l, int r, int s, int t, int d, int f, int& p) {
	if (r < s or t < l) return;
	p = ++tot, ls[p] = ls[f], rs[p] = rs[f], tag[p] = tag[f], sum[p] = sum[f];
	if (l <= s and t <= r) { tag[p] += d, sum[p] += (t - s + 1) * d; return; } int mid = (s + t) >> 1;
	Modify(l, r, s, mid, d, ls[f], ls[p]), Modify(l, r, mid + 1, t, d, rs[f], rs[p]); PushUp(p, s, t);
}
ll Query(int l, int r, int s, int t, ll tg, int p) {
	if (!p or r < s or t < l) return 0;
	if (l <= s and t <= r) return tg * (t - s + 1) + sum[p]; tg += tag[p]; int mid = (s + t) >> 1;
	return Query(l, r, s, mid, tg, ls[p]) + Query(l, r, mid + 1, t, tg, rs[p]);
}

int main() {
	std::ios::sync_with_stdio(false), std::cin.tie(nullptr), std::cout.tie(nullptr);
	std::cin >> n >> m;
	lep(i, 1, n) std::cin >> a[i]; Build(1, n, rt[0]);
	int l, r, d; char op;
	while (m--) {
		std::cin >> op;
		if (op == 'C') std::cin >> l >> r >> d, ++t, Modify(l, r, 1, n, d, rt[t - 1], rt[t]);
		else if (op == 'Q') std::cin >> l >> r, printf("%lld\n", Query(l, r, 1, n, 0, rt[t]));
		else if (op == 'H') std::cin >> l >> r >> d, printf("%lld\n", Query(l, r, 1, n, 0, rt[d]));
		else std::cin >> d, t = d;
	}

	return 0;
}

P8528 [Ynoi2003] 铃原露露

\(\boldsymbol{dsu\_on\_tree ， 吉司机线段树， 容斥}\) 。

正难则反。
考虑什么样的区间无法造成贡献。

对于两个点 \(x\) , \(y\) 的 \(LCA\) \(z\) ，

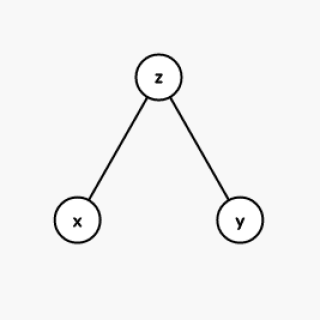
如果 \(x < y < z\) , 那么满足 \(l\le x\) \(\wedge\) \(y\le r < z\) 的区间不合法。
如果 \(z < y < x\) , 那么满足 \(z < l \le y\) \(\wedge\) \(r\ge x\) 的区间不合法。

同时，所有 \(l > r\) 的区间不合法。
将所有不合法的区间看做矩形覆盖。
每次询问相当于二维数 \(0\) 的个数。

看到子区间问题考虑历史版本和，同时，我们可以用最小值来刻画 \(0\) 。
吉司机线段树即可。

现在来考虑如何获得所有的矩形。
先固定 \(z\) ，然后对于每个子树，考虑和之前子树内的前驱和后继，然后发现可以保留下一个子树。
dsu on tree 统计即可。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 2e5 + 7;
typedef long long ll;

struct Info {
	ll ans; int mn, mnc, l, r;
	Info(ll _ans = 0, int _mn = 0, int _mnc = 0, int _l = 0, int _r = 0) { ans = _ans, mn = _mn, mnc = _mnc, l = _l, r = _r; }
	friend Info operator + (const Info& x, const Info& y) {
		if (x.mn < y.mn) return Info(x.ans + y.ans, x.mn, x.mnc, x.l, y.r);
		if (y.mn < x.mn) return Info(x.ans + y.ans, y.mn, y.mnc, x.l, y.r);
		return Info(x.ans + y.ans, x.mn, x.mnc + y.mnc, x.l, y.r);
	}
}tr[_ << 2];
struct Tag {
	int tc, add;
	Tag(int _tc = 0, int _add = 0) { tc = _tc, add = _add; }
	friend Tag operator + (const Tag& x, const Tag& y) { return Tag(x.tc + y.tc, x.add + y.add); }
	bool NE() { return tc or add; }
	Tag ex() { return Tag(0, add); }
}tag[_ << 2];
Info operator * (const Info& x, const Tag& y) { return Info(x.ans + x.mnc * y.tc, x.mn + y.add, x.mnc, x.l, x.r); }

struct node { int l, r, op; }q[_];
int n, m, a[_], fa[_], rt, sz[_], son[_];
std::vector <int> e[_];
std::set <int> S, T; ll ans[_];
std::vector <node> Q[_];

#define ls p << 1
#define rs p << 1 | 1
void PushUp(int p) { tr[p] = tr[ls] + tr[rs]; }
void UpdVal(int p, const Tag& k) { tr[p] = tr[p] * k, tag[p] = tag[p] + k; }
void PushDown(int p) { 
	if (tag[p].NE()) { int l = tr[ls].mn, r = tr[rs].mn;
		if (l <= r) UpdVal(ls, tag[p]);
		else UpdVal(ls, tag[p].ex());
		if (r <= l) UpdVal(rs, tag[p]);
		else UpdVal(rs, tag[p].ex());
		tag[p] = Tag(); 
	}
}
void Build(int l, int r, int p) {
	if (l == r) return tr[p] = { 0, 0, 1, l, l }, void(); int mid = (l + r) >> 1;
	Build(l, mid, ls), Build(mid + 1, r, rs); PushUp(p);
}
void Modify(int l, int r, const Tag& k, int p) {
	if (r < tr[p].l or tr[p].r < l) return;
	if (l <= tr[p].l and tr[p].r <= r) {
		if (k.tc and tr[p].mn != 0) return;
		return UpdVal(p, k); 
	} PushDown(p);
	Modify(l, r, k, ls), Modify(l, r, k, rs); PushUp(p);
}
Info Query(int l, int r, int p) {
	if (l <= tr[p].l and tr[p].r <= r) return tr[p]; PushDown(p);
	if (r <= tr[ls].r) return Query(l, r, ls); if (tr[rs].l <= l) return Query(l, r, rs);
	return Query(l, r, ls) + Query(l, r, rs);
}
#undef ls
#undef rs

void Init(int u) {
	sz[u] = 1;
	for (int v : e[u]) {
		Init(v), sz[u] += sz[v];
		if (sz[v] > sz[son[u]]) son[u] = v;
	}
}
void Merge() {
	if (S.size() < T.size()) std::swap(S, T);
	for (int v : T) S.insert(v); T.clear();
}
void Dfs(int u, int z) {
	T.insert(u);
	auto p = S.lower_bound(u), q = p;
	if (p != S.begin()) { --p;
		if (u < z) Q[u].push_back((node){ 1, *p, 1 }), Q[z].push_back((node){ 1, *p, -1 });
		if (z < *p) Q[u].push_back((node){ z + 1, *p, 1 });
	}
	if (q != S.end()) {
		if (*q < z) Q[*q].push_back((node){ 1, u, 1 }), Q[z].push_back((node){ 1, u, -1 });
		if (z < u) Q[*q].push_back((node){ z + 1, u, 1 });
	}
	for (int v : e[u]) Dfs(v, z);
}
void Solve(int u, bool del) {
	for (int v : e[u]) if (v != son[u]) Solve(v, true);
	if (son[u]) Solve(son[u], false);
	S.insert(u);
	for (int v : e[u]) if (v != son[u]) Dfs(v, u), Merge();
	if (del) S.clear();
}
void Add(int x) {
	for (auto k : Q[x]) Modify(k.l, k.r, Tag(0, k.op), 1);
	Modify(1, x, Tag(1), 1);
}

int main() {
	scanf("%d%d", & n, & m); Build(1, n, 1);
	lep(i, 1, n) scanf("%d", a + i);
	lep(i, 2, n) scanf("%d", fa + i), e[a[fa[i]]].push_back(a[i]);
	rt = a[fa[2]];
	Init(rt), Solve(rt, false); int l, r;
	lep(i, 1, m) scanf("%d%d", & l, & r), q[i] = { l, r, i };

	std::sort(q + 1, q + 1 + m, [](const node& x, const node& y) { return x.r < y.r; });
	int R = 0;
	lep(i, 1, m) {
		while (R < q[i].r) Add(++R);
		ans[q[i].op] += Query(q[i].l, q[i].r, 1).ans;
	}
	lep(i, 1, m) printf("%lld\n", ans[i]);
	return 0;
}

P6220 [COCI 2019/2020 #6] Skandi

\(\boldsymbol{二分图最大匹配，König 定理}\) 。

每个 \(0\) 节点合法有两种可能，一是左侧的 \(1\) 向右，二是上面的 \(1\) 向下。
将每个 \(1\) 向右和向下两种操作拆成两部点，每个 \(0\) 相当于一条边链接了两部点。
选出一个点集覆盖所有边，最小化点集大小。

最小点覆盖输出方案，我们有 \(König\) 定理。
具体的，先求出最大匹配，然后对于每个未被匹配的右部点，遍历所有的交错路，标记沿途的所有点。
最后，被标记的左部点和未被标记的右部点即最小点覆盖集。
交错路指的是，从左往右走匹配边，从右往左走非匹配边。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 1e3 + 7;

int n, m, a[_][_], col[_], row[_], mtc[_ * _], uid[_ * _], ans;
std::vector <int> e[_ * _];
std::bitset <_ * _> vis, un;

int id(int op, int x, int y) { return op * n * m + (x - 1) * m + y; }
void Add(int x, int y) { e[x].push_back(y), e[y].push_back(x); }
bool Dfs(int u) {
	for (int v : e[u]) {
		if (vis[v]) continue; vis[v] = true;
		if (!mtc[v] or Dfs(mtc[v])) {
			mtc[v] = u, uid[u] = v;
			return true;
		}
	}
	return false;
}
void Sgn(int u) {
	un[u] = true;
	if (u <= n * m) {
		if (uid[u]) Sgn(uid[u]); 
		return;
	}
	for (int v : e[u]) 
		if (v != mtc[u] and !un[v])
			Sgn(v);
}

int main() {
	scanf("%d%d", & n, & m);
	lep(i, 1, n) lep(j, 1, m) scanf("%1d", a[i] + j);
	lep(i, 1, n) {
		lep(j, 1, m) {
			if (a[i][j]) row[i] = col[j] = id(0, i, j);
			else Add(row[i], col[j] + n * m);
		}
	}
	lep(i, 1, n) lep(j, 1, m) if (a[i][j] and Dfs(id(0, i, j))) vis.reset(), ++ans;
	lep(i, 1, n) lep(j, 1, m) 
		if (a[i][j] and !mtc[id(1, i, j)]) Sgn(id(1, i, j));
	printf("%d\n", ans);
	lep(i, 1, n) lep(j, 1, m) if (a[i][j]) {
		if (un[id(0, i, j)]) printf("%d %d DESNO\n", i, j);
		if (!un[id(1, i, j)]) printf("%d %d DOLJE\n", i, j);
	}
	return 0;
}

AT_arc076_d [ARC076F] Exhausted?

\(\boldsymbol{Hall 定理}\) 。

对于一张二分图，定义 \(S\) 为左部点中的任意点集， \(N(S)\) 为与这个点集中的至少一个点相连的点。
设左部点有 \(n\) 个，右部点有 \(m\) 个。
则最大匹配数 = \(n - \max\{0, n - m, \max\{|S|-|N(S)|\}\}\) 。

这个题目要求我们求后面的部分。
即我们现在有若干组上界和下界，选出其中的一部分，最大化 选出的组数 - 所有组的并。
根据德摩根定律，我们现在的问题变成了：
有 \(m\) 条线段，选出 \(k\) 条线段，最大化 \(k - m + \bigcap_{i=1}^k [l_i, r_r]\) 。

我们并不好刻画若干条线段的交，所以我们直接枚举交。
固定当前交区间的左端点 \(L\)，对于一个右端点 \(R\) ，其贡献为 \(R - L + 1 - m + \sum_i[l_i\le L \wedge R \le r_i]\) 。
扫描线，将满足 \(l \le L\) 的线段插入一个数据结构，现在我们要最大化 \(R + \sum_i{r_i\ge R}\) 。
初始每个位置 \(i\) 的值都是 \(i\) ，每插入一条线段，就讲 \(r\) 这个前缀的值都 \(+1\) 。
线段树即可。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 2e5 + 7;
typedef long long ll;

int n, m, ans, c[_];
int mx[_ << 2], tag[_ << 2];
std::vector <int> q[_];

#define ls p << 1
#define rs p << 1 | 1
void PushUp(int p) { mx[p] = std::max(mx[ls], mx[rs]); }
void Build(int l, int r, int p) {
	if (l == r) { mx[p] = l; return; } int mid = (l + r) >> 1;
	Build(l, mid, ls), Build(mid + 1, r, rs); PushUp(p);
}
void Upd(int p, int k) { mx[p] += k, tag[p] += k; }
void PushDown(int p) { if (tag[p]) Upd(ls, tag[p]), Upd(rs, tag[p]), tag[p] = 0; }
void Modify(int l, int r, int s, int t, int k, int p) {
	if (r < s or t < l) return;
	if (l <= s and t <= r) return Upd(p, k); PushDown(p); int mid = (s + t) >> 1;
	Modify(l, r, s, mid, k, ls), Modify(l, r, mid + 1, t, k, rs); PushUp(p);
}
int Query(int l, int r, int s, int t, int p) {
	if (r < s or t < l) return 0;
	if (l <= s and t <= r) return mx[p]; PushDown(p); int mid = (s + t) >> 1;
	return std::max(Query(l, r, s, mid, ls), Query(l, r, mid + 1, t, rs));
}
#undef ls
#undef rs

int main() {
	scanf("%d%d", & n, & m); int l, r; Build(1, m, 1);
	lep(i, 1, n) {
		scanf("%d%d", & l, & r); 
		if (l + 1 < r) q[l + 1].push_back(r - 1);
	}
	lep(l, 1, m) {
		for (int r : q[l]) Modify(l, r, 1, m, 1, 1);
		ans = std::max(ans, Query(l, r, 1, m, 1) + 1 - l - m);
	}
	ans = std::max(n - m, ans);
	printf("%d\n", ans);
	return 0;
}

P5443 [APIO2019] 桥梁

\(\boldsymbol{根号重构}\) 。

每 \(B\) 个修改操作一组，统一处理之间的询问。
对于这个题来说，先将修改未涉及的符合条件的边加入图，然后枚举被修改的边，如果符合条件就加入。
注意同一条边可能被修改多次，所以应该判断时间上符合条件的（同一条）边中最后加入的是否合法。
如果在询问前为修改这条边，则按照其初始值是否合法加入。
每统一处理完一次，进行所有修改操作。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 4e6 + 7;
typedef long long ll;
typedef std::bitset <_> Bit;

struct edge { int u, v, d; }e[_];
struct node { int op, b, r, t; }o[_], q[_]; int Q;
int n, m, fa[_], sz[_], qry, id[_]; Bit ch;
int stk[_], top, bot, ans[_], lst[_];

int Find(int x) { return fa[x] == x ? x : Find(fa[x]); }
void Merge(int x, int y) {
	if ((x = Find(x)) != (y = Find(y))) {
		if (sz[x] > sz[y]) std::swap(x, y);
		stk[++top] = x, fa[x] = y, sz[y] += sz[x];
	}
}
void Back() { int x;
	while (top != bot)
		x = stk[top--], sz[fa[x]] -= sz[x], fa[x] = x;
}

int main() {
	scanf("%d%d", & n, & m);
	lep(i, 1, m) scanf("%d%d%d", & e[i].u, & e[i].v, & e[i].d), id[i] = i;

	scanf("%d", & qry); int B = 1500, op, tim0 = 0, tim1 = 0;
	lep(Q, 1, qry) { 
		scanf("%d", & op);
		if (op == 1) ++tim0, scanf("%d%d", & o[tim0].b, & o[tim0].r), o[tim0].t = Q, ch[o[tim0].b] = true;
		else ++tim1, scanf("%d%d", & q[tim1].b, & q[tim1].r), q[tim1].t = Q;
		if (Q == qry or tim0 + tim1 == B) {
			lep(i, 1, n) fa[i] = i, sz[i] = 1;
			std::sort(id + 1, id + 1 + m, [](const int& x, const int& y) {
					return e[x].d > e[y].d;
			});
			auto cmp = [](const node&x, const node& y) { return x.r > y.r; };
			std::sort(o + 1, o + tim0 + 1, cmp), std::sort(q + 1, q + tim1 + 1, cmp);

			int R = 1;
			lep(i, 1, tim1) {
				while (R <= m and (e[id[R]].d >= q[i].r or ch[id[R]])) {
					if (!ch[id[R]]) Merge(e[id[R]].u, e[id[R]].v);
					++R;
				} bot = top;
				lep(j, 1, tim0) if (o[j].t < q[i].t) lst[o[j].b] = std::max(lst[o[j].b], o[j].t);
				lep(j, 1, tim0) {
					if (o[j].r >= q[i].r and o[j].t == lst[o[j].b]) Merge(e[o[j].b].u, e[o[j].b].v);
					else if (!lst[o[j].b] and e[o[j].b].d >= q[i].r) Merge(e[o[j].b].u, e[o[j].b].v);
				}
				lep(j, 1, tim0) lst[o[j].b] = 0;
				ans[q[i].t] = sz[Find(q[i].b)]; Back();
			}

			std::sort(o + 1, o + tim0 + 1, [](const node&x, const node&y) { return x.t < y.t; });
			lep(i, 1, tim0) e[o[i].b].d = o[i].r;
			ch.reset(), tim0 = tim1 = top = 0;
		}
	}

	lep(i, 1, qry) if (ans[i]) printf("%d\n", ans[i]);
	return 0;
}

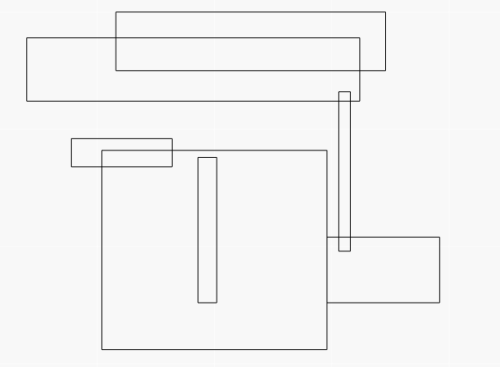
P2137 Gty的妹子树

\(\boldsymbol{树分块}\) 。

我们规定，每个块的大小最大为 \(B\) ，块内一定联通。
一条边，如果端点在同一个块内，则称其为实边，否则为虚边。
每个连出虚边的点我们称其为这个块的叶子，被虚边连接的点我们称其为这个块的根。

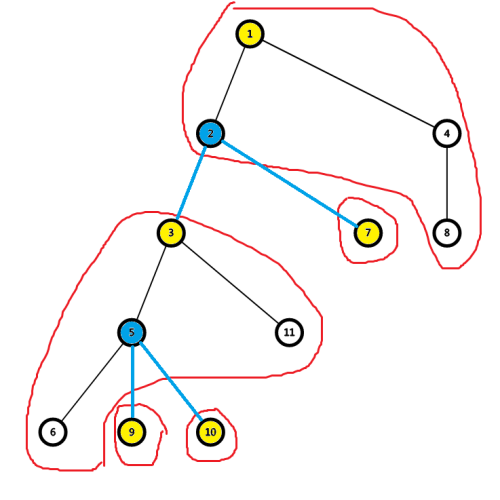
图中是 \(B = 4\) 的一种情况，红色边框起来的就是一个块，黄色点是根，蓝色点是叶子，蓝色边是虚边。

对于每个点维护一个信息集合。
如果其不为叶子，则维护其本身信息。
否则，再加上虚边连出的子树内所有节点的信息。

每次修改一个点，就存储其信息的叶子全部修改。
到根链上最多有 \(\frac{N}{B}\) 条虚边，最多修改 \(\frac{N}{B}\) 次。
查询信息直接遍历所在块内子树的信息集合即可。

连边时，如果父亲所在块大小未达到 \(B\) ，则与父亲归为一个块。
否则，自成一个块，根就是自己。

取 \(B = \sqrt n\) ，则复杂度为 \(O(n\sqrt n \times f(n))\) ， \(f(n)\) 是数据结构的均摊复杂度 。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 2e6 + 7;
typedef long long ll;

int n, m, rt[_], bel[_], cnt[_], scc, a[_], top[_], fa[_], B, ans;
int val[_], rnd[_], ls[_], rs[_], sz[_], tot, x, y, z;
std::vector <int> e[_], g[_];

int New(int x) { ++tot; val[tot] = x, rnd[tot] = rand(), ls[tot] = rs[tot] = 0, sz[tot] = 1; return tot; }
void PushUp(int x) { sz[x] = sz[ls[x]] + sz[rs[x]] + 1; }
void Split(int p, int v, int& x, int& y) {
	if (!p) { x = y = 0; return; }
	if (val[p] <= v) x = p, Split(rs[p], v, rs[x], y);
	else y = p, Split(ls[p], v, x, ls[y]); PushUp(p);
}
void Split_k(int p, int k, int&x, int& y) {
	if (!p) { x = y = 0; return; }
	if (sz[ls[p]] + 1 <= k) x = p, Split_k(rs[p], k - sz[ls[p]] - 1, rs[x], y);
	else y = p, Split_k(ls[p], k, x, ls[y]); PushUp(p);
}
int Merge(int x, int y) {
	if (!x or !y) return x | y;
	if (rnd[x] > rnd[y]) { rs[x] = Merge(rs[x], y), PushUp(x); return x; }
	else { ls[y] = Merge(x, ls[y]), PushUp(y); return y; }
}
void Mdy(int v, int& rt) { Split(rt, v, x, y), rt = Merge(x, Merge(New(v), y)); }
void Del(int v, int& rt) { Split(rt, v - 1, x, z), Split_k(z, 1, y, z), rt = Merge(x, z); }
int Qry(int v, int& rt) { Split(rt, v, x, y); int res = sz[y]; rt = Merge(x, y); return res; }
void Mdy(int u) { int p = u;
	while (fa[top[bel[u]]]) {
		Mdy(a[p], rt[fa[top[bel[u]]]]);
		u = fa[top[bel[u]]];
	}
}
void Del(int u) { int p = u;
	while (fa[top[bel[u]]]) {
		Del(a[p], rt[fa[top[bel[u]]]]);
		u = fa[top[bel[u]]];
	}
}
void Ins(int u, int f) {
	rt[u] = New(a[u]), fa[u] = f; g[f].push_back(u);
	if (f and cnt[bel[f]] < B) bel[u] = bel[f], ++cnt[bel[f]];
	else bel[u] = ++scc, top[scc] = u, cnt[scc] = 1;
	Mdy(u);
}
void Init(int u, int f) {
	Ins(u, f);
	for (int v : e[u]) if (v != f) Init(v, u);
}
int qry(int u, int k) { int res = Qry(k, rt[u]);
	for (int v : g[u]) 
		if (bel[v] == bel[u]) res += qry(v, k);
	return res;
}

int main() {
	scanf("%d", & n); int u, v; B = std::sqrt(n);
	lep(i, 2, n) scanf("%d%d", & u, & v),
		e[u].push_back(v), e[v].push_back(u);
	lep(i, 1, n) scanf("%d", a + i);
	Init(1, 0);
	
	scanf("%d", & m);
	int op, x, y;
	while (m--) {
		scanf("%d%d%d", & op, & x, & y); x ^= ans, y ^= ans;
		if (op == 0) printf("%d\n", ans = qry(x, y));
		else if (op == 1) {
			Del(a[x], rt[x]), Del(x); a[x] = y;
			Mdy(a[x], rt[x]), Mdy(x);
		}
		else a[++n] = y, Ins(n, x);
	}
	return 0;
}

AT_joisc2016_h 回転寿司

\(\boldsymbol{分块，延迟重整}\) 。

ps: 延迟重整是我自己起的名字。

先考虑每次操作，遍历序列，将大于当前值的与当前值交换，一定会得到这个序列的最大值，而其他值会变动位置。
考虑分块，散块暴力统计，整块可以用数据结构查询最大值，然后删去，插入当前值。
但是这样统计散块时顺序就是错误的，我们需要对散块进行重整来保证正确。
现在我们得知了这个块内都有过什么新的元素加入。
这些元素中，最小的元素是不会被其他元素影响的，所以我们优先考虑他。
找到第一个大于他的位置交换。
容易发现，这个位置的值已经固定了，且在他之前的位置一定不会改变（因为这是最小的值）。
并且，尽管这个最小值加入的时间不一定是最早的，但它最终一定会停在这个位置上。
所以我们维护一个小根堆，每次遇到可以交换的就与堆顶交换。
最后将小根堆清空即可。

点击查看

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 4e5 + 7;
typedef long long ll;

int n, q, a[_], block, bel[_], st[_], ed[_];
std::priority_queue <int> B[_];
std::priority_queue <int, std::vector <int>, std::greater<int> > S[_];

void Chg(int x) {
	if (S[x].empty()) return;
	lep(i, st[x], ed[x]) if (a[i] > S[x].top()) 
			S[x].push(a[i]), a[i] = S[x].top(), S[x].pop();
	while (!S[x].empty()) S[x].pop();
}
void SWP(int l, int r, int& y) { 
	lep(i, l, r) if (a[i] > y) std::swap(a[i], y);
	while (!B[bel[l]].empty()) B[bel[l]].pop();
	lep(i, st[bel[l]], ed[bel[l]]) B[bel[l]].push(a[i]);
}
void Upd(int x, int& y) { if (B[x].top() > y) B[x].push(y), S[x].push(y), y = B[x].top(), B[x].pop(); }

int main() {
	scanf("%d%d", & n, & q); block = std::sqrt(n);
	lep(i, 1, n) {
		scanf("%d", a + i), bel[i] = (i - 1) / block + 1;
		B[bel[i]].push(a[i]);
		if (!st[bel[i]]) st[bel[i]] = i; ed[bel[i]] = i;
	} int l, r, x;
	while (q--) {
		scanf("%d%d%d", & l, & r, & x); Chg(bel[l]), Chg(bel[r]);
		if (l <= r) {
			if (bel[l] == bel[r]) SWP(l, r, x);
			else {
				SWP(l, ed[bel[l]], x);
				lep(i, bel[l] + 1, bel[r] - 1) Upd(i, x);
				SWP(st[bel[r]], r, x);
			}
		}
		else {
			SWP(l, ed[bel[l]], x);
			lep(i, bel[l] + 1, bel[n]) Upd(i, x);
			lep(i, 1, bel[r] - 1) Upd(i, x);
			SWP(st[bel[r]], r, x);
		}
		printf("%d\n", x);
	}
	return 0;
}