那快把题端上来吧 （一）
六月训练好题记录
CF1761G - Centroid Guess
\(\boldsymbol{交互、随机化、重心}\)。
如果我们拥有一条经过重心的链，端点是 \(s\) ， \(t\)，可以通过询问 \(2n\) 次每个点分别到 \(s\) , \(t\) 的距离。
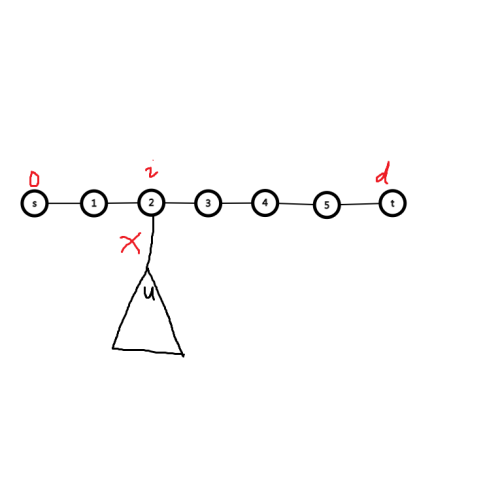
记 \(a=dis(s,u)=i+x, b=dis(u,t)=d-i+x\) ，
则 \(i = \frac{a - b + d}{2}\) ， 对所有的链上的点计数， \(>\frac{n}{2}\) 即为重心。
但如果我们并没有一条经过重心的链呢？
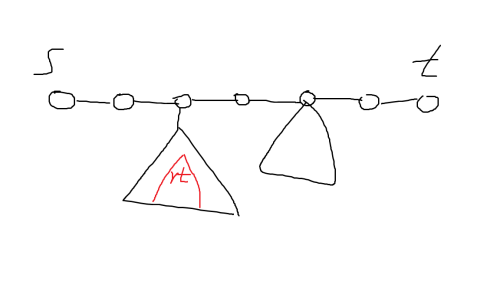
对于我们剩下的 \(50000\) 次询问，随机 \(300\) 个点，如果有超过 \(150\) 个点属于 \(i\) ，那么重心大概率在其中。
在 \(i\) 下方挂着的点中随机一个作为链的端点，总共有 \(\frac{1}{4}\) 的概率经过重心，同时，我们要在 \(s\) 和 \(t\) 中选择离 \(i\) 更近的舍弃，这样才几乎不可能会舍弃掉已有的重心。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 1e5 + 7;
typedef long long ll;
std::mt19937 rd(time(0));
int n, s, t, tot, cnt, sz[_], cur[_], d, a, b;
int tim[_]; std::vector <int> lis[_];
std::map<std::pair<int, int>, int> S;
int Query(int s, int t) {
if (s == t) return 0;
auto nw = std::minmax(s, t);
if (S.count(nw)) return S[nw];
int x; std::cout << "? " << s << ' ' << t << std::endl;
std::cin >> x; return S[nw] = x;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n; s = 1, t = n, tot = 70;
while (tot--) {
cnt = 316; d = Query(s, t);
while (cnt--) {
int x = rd() % n + 1;
a = Query(s, x), b = Query(x, t);
int pos = (a - b + d) / 2;
lis[pos].push_back(x);
}
lep(i, 0, d) if (lis[i].size() > 170) {
int u = rd() % lis[i].size();
i >= d / 2 ? t = lis[i][u] : s = lis[i][u];
break;
}
lep(i, 0, d) tim[i] = 0, lis[i].clear();
}
d = Query(s, t);
lep(x, 1, n) {
a = Query(s, x), b = Query(x, t);
int dep = (a + b - d) / 2, pos = (a - b + d) / 2; ++sz[pos];
if (!dep) cur[pos] = x;
}
int sum = 0;
lep(i, 0, d) { sum += sz[i];
if (sum > n / 2) {
std::cout << "! " << cur[i] << std::endl;
return 0;
}
}
puts("! 1");
return 0;
}
CF1844G - Tree Weights
\(\boldsymbol{数值倍增法}\) 。
注意到，
\[d_i=len_i+len_{i-1}-2\times len_{LCA(i, i+1)}
\]
其中， \(len_i\) 表示 \(i\) 的到根路径权值和。同时，我们发现：
\[d_i\equiv len_i+len_{i-1}\pmod 2
\]
如果以 \(1\) 为根，我们便可以递推出所有的 \(len_i \bmod 2\) 。
由此，我们有 ：
\[d_i\bmod 2^k = len_i \bmod 2^k + len_{i+1}\bmod 2^k - 2\times (len_{LCA}\bmod 2^{k-1})\\
\therefore
len_{i+1}\bmod 2^k = d_i\bmod 2^k - len_i \bmod 2^k + 2\times (len_{LCA}\bmod 2^{k-1})
\]
递推即可。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 2e5 + 7;
typedef long long ll;
int n, lca[_], fa[_][21], dep[_]; ll d[_], len[_], Mod[100], ans[_];
std::vector <int> e[_];
std::map<std::pair<int, int>, int> id;
void Init(int u, int f) {
dep[u] = dep[fa[u][0] = f] + 1;
lep(i, 1, 20) fa[u][i] = fa[fa[u][i - 1]][i - 1];
for (int v : e[u]) if (v != f) Init(v, u);
}
int LCA(int x, int y) {
if (dep[x] < dep[y]) std::swap(x, y);
rep(i, 20, 0) if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
if (x == y) return x;
rep(i, 20, 0) if (fa[x][i] != fa[y][i])
x = fa[x][i], y = fa[y][i];
return fa[x][0];
}
void Solve(int u, int f) {
for (int v : e[u]) if (v != f) {
if (len[v] <= len[u] or len[v] - len[u] > 1e12) { puts("-1"); exit(0); }
ans[id[std::minmax(u, v)]] = len[v] - len[u];
Solve(v, u);
}
}
int main() {
scanf("%d", & n); int u, v;
lep(i, 1, n - 1) scanf("%d%d", & u, & v),
e[u].push_back(v), e[v].push_back(u), id[std::minmax(u, v)] = i;
Init(1, 0);
lep(i, 1, n - 1) scanf("%lld", d + i), lca[i] = LCA(i, i + 1);
lep(i, 1, 60) Mod[i] = (Mod[i - 1] << 1) | 1;
lep(k, 1, 60) {
lep(i, 1, n - 1) len[i + 1] =
((d[i] & Mod[k]) - (len[i] & Mod[k]) +
((len[lca[i]] & Mod[k - 1]) << 1)) & Mod[k];
}
Solve(1, 0);
lep(i, 1, n - 1) printf("%lld\n", ans[i]);
return 0;
}
Luogu P9523 [JOISC 2022] 复制粘贴 3
\(\boldsymbol{DP}\) 。
首先发现，剪切粘贴的一定是原串的子串。
设计 \(dp[l,r,i, j]\) 为输入 \(s[l,r]\) ，当前剪贴板为 \(s[i,j]\) 。
转移发现存储剪贴板内容是没必要的，因为我们发现拼终串时只会用到一次剪切与若干次粘贴，需要 \(dp\) 的部分是用来剪切的串可能同样是这样拼出来的。
所以设计状态 \(dp[l,r]\) 表示拼出 \(s[l,r]\) 的最小代价，然后由小到大地进行转移。
根据转移，我们需要得知子串 \([l,r]\) 下一个相同子串的位置，提前预处理后缀的 \(LCP\)，注意不能重合。
然后取前缀 \(Max\) ，就具有了单调性，可以二分这个位置。
转移时由调和级数可得，总复杂度为 \(O(n^2\log n)\) 。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 2500 + 7;
typedef long long ll;
int n, lk[_][_], nxt[_][_]; char s[_];
ll dp[_][_], A, B, C;
int main() {
scanf("%d%s%lld%lld%lld", & n, s + 1, & A, & B, & C);
rep(j, n, 1) rep(i, j, 1) {
if (s[i] == s[j]) nxt[i][j] = nxt[i + 1][j + 1] + 1;
nxt[i][j] = std::min(nxt[i][j], j - i);
}
lep(i, 1, n) lep(j, i, n) nxt[i][j] = std::max(nxt[i][j], nxt[i][j - 1]);
lep(i, 1, n) lep(j, i, n) { int l = j + 1, r = n + 1;
while (l < r) { int mid = (l + r) >> 1;
if (nxt[i][mid] >= j - i + 1) r = mid;
else l = mid + 1;
}
lk[i][j] = l, dp[i][j] = 1e18;
}
lep(i, 1, n) dp[i][i] = A;
lep(len, 1, n) lep(l, 1, n - len + 1) { int r = l + len - 1;
if (l < r) dp[l][r] = std::min(std::min(dp[l + 1][r], dp[l][r - 1]) + A, dp[l][r]);
int p = l, t = 1;
while (p <= n) {
dp[l][p + (r - l)] = std::min(dp[l][p + (r - l)],
dp[l][r] + B + t * C + A * (p + (r - l) - l + 1 - t * (r - l + 1)));
p = lk[p][p + (r - l)], ++t;
}
}
printf("%lld\n", dp[1][n]);
return 0;
}
Luogu P3191 紧急疏散
\(\boldsymbol{二分答案、网络流建模}\)。
对于每扇门每秒钟只能通行一个人的限制，我们对时间拆点。
如图：
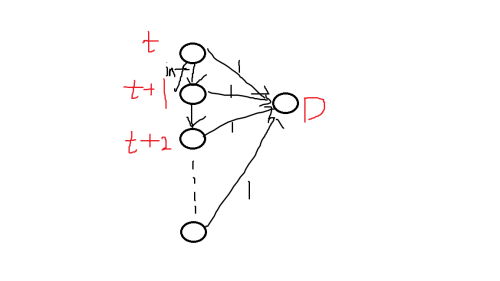
每一秒向下一秒连 \(inf\) 边，向终点连 \(1\) 边，终点向汇点连 \(inf\) 边。
源点向每个空地、每个空地向对应的时间连 \(1\) 边。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)
typedef long long ll;
typedef std::pair<int, int> PII;
const int _ = 1e5 + 7;
const int inf = 2e9;
struct edge { int v, c, n; }e[_]; int H[_], cur[_], cnte = 1;
int n, m, S, T, idx, tim[401][401], to[401][401], rtim[_]; int dep[_]; char s[25][25];
int di[4] = { 0, 0, 1, -1 };
int dj[4] = { 1, -1, 0, 0 };
std::map<PII, int> ID; std::vector <int> Bg, Ed;
void Add(int u, int v, int c) { e[++cnte] = { v, c, H[u] }, H[u] = cnte; e[++cnte] = { u, 0, H[v] }, H[v] = cnte; }
bool Bfs() { std::queue <int> d;
lep(i, S, T) dep[i] = 0; dep[S] = 1;
d.push(S);
while (!d.empty()) {
int u = d.front(); d.pop();
if (u == T) return true;
ep(i, u, v) if (e[i].c > 0 and !dep[v])
dep[v] = dep[u] + 1, d.push(v);
}
return false;
}
int Dfs(int u, int flow) {
if (u == T or !flow) return flow;
int res = 0, f;
ep(i, u, v) { H[u] = i;
if (dep[v] != dep[u] + 1 or !e[i].c) continue;
if (!flow) break;
f = Dfs(v, std::min(flow, e[i].c));
if (!f) { dep[v] = 0; continue; }
e[i].c -= f, e[i ^ 1].c += f, res += f, flow -= f;
} return res;
}
int Dinic() { int ans = 0;
lep(i, S, T) cur[i] = H[i];
while (Bfs()) {
ans += Dfs(S, inf);
lep(i, S, T) H[i] = cur[i];
} return ans;
}
inline int Hash(int x, int y) { return ID[{x, y}] ? ID[{x, y}] : ID[{x, y}] = ++idx; }
void Solve(int x, int y) { std::queue <PII> d; d.push({x, y}), Ed.push_back(Hash(x, y));
lep(i, 2, n - 1) lep(j, 2, m - 1) tim[i][j] = 0;
while (!d.empty()) {
int x = d.front().first, y = d.front().second; d.pop();
lep(k, 0, 3) {
int dx = x + di[k], dy = y + dj[k];
if (dx < 1 or dx > n or dy < 1 or dy > m or tim[dx][dy] or s[dx][dy] != '.') continue;
tim[dx][dy] = tim[x][y] + 1, d.push({dx, dy});
}
}
lep(i, 1, n) lep(j, 1, m) if (s[i][j] == '.') {
to[Hash(i, j)][Hash(x, y)] = tim[i][j];
}
}
bool Check(int lim) {
lep(i, S, T) H[i] = 0; cnte = 1;
for (int st : Bg) {
Add(S, st, 1);
for (int ed : Ed) if (to[st][ed])
Add(st, Hash(n + ed, to[st][ed]), 1);
}
for (int ed : Ed) {
lep(i, 1, lim) {
Add(Hash(n + ed, i), ed, 1);
if (i != lim) Add(Hash(n + ed, i), Hash(n + ed, i + 1), inf);
}
} T = idx + 1;
for (int ed : Ed) Add(ed, T, inf);
return Dinic() == Bg.size();
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, n) scanf("%s", s[i] + 1);
lep(i, 1, n) lep(j, 1, m) {
if (s[i][j] == '.') Bg.push_back(Hash(i, j));
else if (s[i][j] == 'D') Solve(i, j);
}
int l = 1, r = n * m + 1;
while (l < r) { int mid = (l + r) >> 1;
if (Check(mid)) r = mid;
else l = mid + 1;
}
if (l == n * m + 1) puts("impossible");
else printf("%d\n", l);
return 0;
}
Luogu P12506 「ROI 2025 Day2」沼泽里的青蛙
\(\boldsymbol{分块}\) 。
题意即判断每个点是否与某个奇环连通。
按照 \(\frac{r}{\sqrt 2}\) 将两维值域分块，在同一块内的点相互之间一定可达。
我们将点数 \(\ge 3\) 的块称为重块， \(< 3\) 的称为轻块。
重块内的点全部合法，对于每个轻块，将其与以此块为中心的 \(5\times 5\) 的块处理连边。
然后判断奇环连通性即可。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
typedef long long ll;
typedef double D;
typedef std::pair<int, int> PII;
const int _ = 1e5 + 7;
const D s2 = std::sqrt(2);
int n; D r, x[_], y[_], fa[_], col[_]; bool ans[_], vis[_];
std::map<PII, int> ID;
std::map<PII, bool>Lk;
std::vector <int> lt[_], e[_]; int idx;
int Hash(int x, int y) { return ID[{x, y}] ? ID[{x, y}] : ID[{x, y}] = ++idx; }
void Add(int id) {
int X = std::ceil(x[id] / (r / s2)), Y = std::ceil(y[id] / (r / s2));
lt[Hash(X, Y)].push_back(id);
}
D Dis(int a, int b) { return (x[a] - x[b]) * (x[a] - x[b]) + (y[a] - y[b]) * (y[a] - y[b]); }
void Link(int x, int y) {
if (Lk[std::minmax(x, y)]) return;
Lk[std::minmax(x, y)] = true;
if (ans[x]) ans[y] = true;
else if (ans[y]) ans[x] = true;
else e[x].push_back(y), e[y].push_back(x);
}
bool Dfs(int u, int f, int c) {
if (ans[u]) return true;
if (col[u]) return (col[u] != c);
col[u] = c;
for (int v : e[u]) if (v != f)
if (Dfs(v, u, -c)) return true;
return false;
}
void Paint(int u) {
vis[u] = ans[u] = true;
for (int v : e[u]) if (!vis[v]) Paint(v);
}
int main() {
scanf("%d%lf", & n, & r);
lep(i, 1, n) scanf("%lf%lf", x + i, y + i), Add(i);
for (auto I : ID) {
int X = I.first.first, Y = I.first.second, i = I.second;
if (lt[i].size() >= 3) for (int k : lt[i]) ans[k] = true;
else for (int k : lt[i]) for (int l : lt[i]) if (k < l) Link(k, l);
lep(dx, X - 2, X + 2) lep(dy, Y - 2, Y + 2) if (ID.count({dx, dy})) {
if (lt[ID[{dx, dy}]].size() >= 3 and lt[i].size() >= 3) continue;
if (ID[{dx, dy}] == i) continue;
for (int k : lt[ID[{dx, dy}]]) for (int l : lt[i])
if (Dis(k, l) <= r * r) Link(k, l);
}
}
lep(i, 1, n) if (!col[i])
if (Dfs(i, 0, 1)) Paint(i);
lep(i, 1, n) putchar(ans[i] ? '1' : '0');
return 0;
}
时间仓促，如有错误欢迎指出，欢迎在评论区讨论，如对您有帮助还请点个推荐、关注支持一下
浙公网安备 33010602011771号