算法笔记 - 虚树

引入

[SDOI2011] 消耗战

给出一棵树和若干次询问。
每次给定一些关键点（保证不包含根），要求切断一些边使根节点与任意一个关键点不连通，最小化代价。
询问总点数 \(2.5\times 10^5\) 数量级。

对于每次询问容易想出一个 \(O(n)\) 的 \(DP\) ，发现这个 \(DP\) 我们只关心关键点和他们的 \(LCA\)，以及所有关键点 \(LCA\) 的到根路径，由此引入我们的崭新工具。

虚树概述

当我们发现同时处理整棵树复杂度难以接受，我们就想要
将一棵树中的关键节点从原树中分离出来单独处理，控制复杂度与 \(\boldsymbol{总询问节点个数}\) 相关。

构建

我们通过模拟 \(Dfs\) 的过程来构建虚树。
用栈维护一条虚树上深度递增的链。
将所有关键点按 \(Dfs\) 序排序，依次处理。

先将根节点入栈。
对于依次处理的每一个 \(x\)，记它与栈顶元素 \(top\) 的 \(LCA\) 为 \(lca\) 。
若 \(lca = top\) ，则说明 \(x\) 应该接在栈链的后面，不做额外处理。

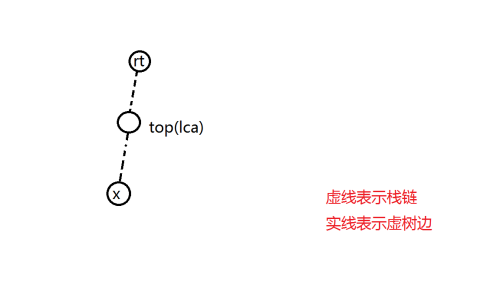
如果 \(lca \ne top\) ，则说明 \(x\) 在栈链的支链上。

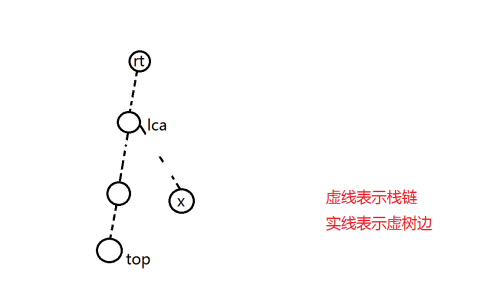
尝试找到 \(lca\) 所在的分界点，记栈顶的下一位元素为 \(next\) 。
若 \(next\) 的深度大于 \(lca\) ，则连接 \(next\) 与 \(top\) ，同时弹掉栈顶。

重复此过程会得到两种可能结果

分界点在栈内

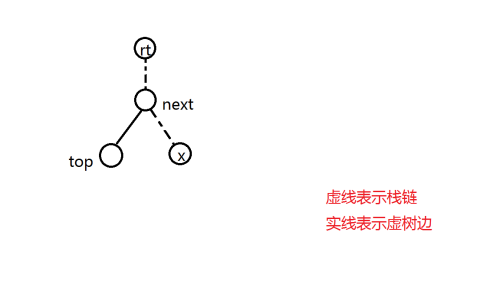
连接 \(next\) 与 \(top\) ，弹掉栈顶。

分界点不在栈内

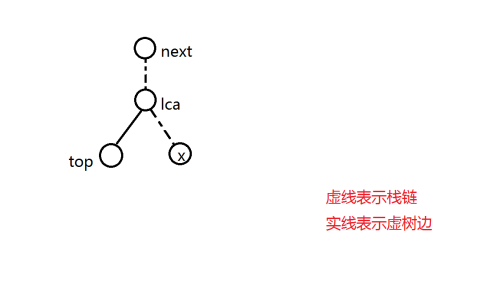
连接 \(lca\) 与 \(top\)，弹掉栈顶，将 \(lca\) 入栈。

最后将 \(x\) 入栈。

将所有关键点入栈后，把剩下的一条栈链加入虚树。

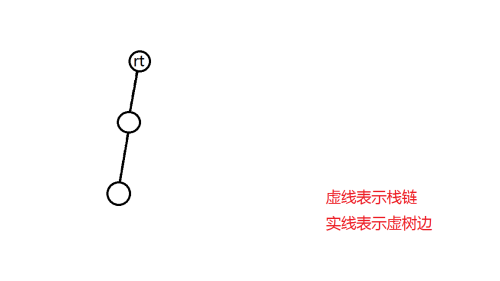
实现中注意，每次有一个节点入栈的时候，要清空其所存储的上一棵虚树的信息。

点击查看


void Build() {
    std::sort(h + 1, h + 1 + k, [](int x, int y) { return dfn[x] < dfn[y]; });
    stk[top = 1] = 1, g[1].clear();
    lep(i, 1, k) if (h[i] != 1) { un[h[i]] = true;
        int l = LCA(stk[top], h[i]);
        if (l != stk[top]) {
            while (dep[l] < dep[stk[top - 1]])
                Add(stk[top - 1], stk[top]), --top;
            if (l != stk[top - 1])
                g[l].clear(), Add(l, stk[top]), stk[top] = l;
            else Add(l, stk[top--]);
        }
        stk[++top] = h[i], g[h[i]].clear();
    } else un[1] = true;
    lep(i, 1, top - 1) Add(stk[i], stk[i + 1]);
}

例题

[SDOI2011] 消耗战

给出一棵树和若干次询问，每次给定一些关键点（保证不包含根），要求切断一些边使根节点与任意一个关键点不连通，最小化代价。
询问总点数 \(2.5\times 10^5\) 数量级。

点击查看

思路见上，倍增处理 \(LCA\) 及两点间最小边权。


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)

typedef long long ll;
typedef std::pair<int, int> PII;
const int _ = 5e5 + 7;
const int inf = 2e9;

struct Edge { int v, n, w; } e[_]; int H[_], cnte = 1;
int n, m, k, h[_], dfn[_], idx; ll f[_];
int dep[_], fa[_][20], len[_][20], stk[_], top;
std::vector <int> g[_]; bool vis[_];

void Add(int u, int v, int w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void Init(int u, int f) {
    dfn[u] = ++idx, dep[u] = dep[f] + 1;
    lep(i, 1, 19)
        fa[u][i] = fa[fa[u][i - 1]][i - 1],
        len[u][i] = std::min(len[u][i - 1], len[fa[u][i - 1]][i - 1]);
    ep(i, u, v) if (v != f) {
        fa[v][0] = u, len[v][0] = e[i].w;
        Init(v, u);
    }
}
PII Query(int x, int y) {
    int res = inf;
    if (dep[x] < dep[y]) std::swap(x, y);
    rep(i, 19, 0) if (dep[fa[x][i]] >= dep[y])
        res = std::min(res, len[x][i]), x = fa[x][i];
    if (x == y) return { x, res };
    
    rep(i, 19, 0) if (fa[x][i] != fa[y][i])
        res = std::min(res, len[x][i]),
        res = std::min(res, len[y][i]),
        x = fa[x][i], y = fa[y][i];
    return { fa[x][0], res };
}
void Build() {
    stk[top = 1] = 1; g[1].clear();
    std::sort(h + 1, h + 1 + k, [](int x, int y) { return dfn[x] < dfn[y]; });
    lep(i, 1, k) { vis[h[i]] = true;
        int lca = Query(h[i], stk[top]).first;
        if (lca != stk[top]) {
            while (dfn[stk[top - 1]] > dfn[lca])
                g[stk[top - 1]].push_back(stk[top]), --top;
            if (stk[top - 1] != lca)
                g[lca].clear(), g[lca].push_back(stk[top]), stk[top] = lca;
            else g[lca].push_back(stk[top--]);
        }
        g[h[i]].clear(), stk[++top] = h[i];
    }
    lep(i, 1, top - 1)
        g[stk[i]].push_back(stk[i + 1]);
}
void Solve(int u) {
    f[u] = 0;
    for (int v : g[u]) {
        Solve(v); ll w = Query(u, v).second;
        if (vis[v]) f[u] += w;
        else f[u] += std::min(w, f[v]);
    }
}
void Clear() { lep(i, 1, k) vis[h[i]] = false; }

int main() {
    scanf("%d", & n); int u, v, w;
    lep(i, 1, n - 1) scanf("%d%d%d", & u, & v, & w),
        Add(u, v, w), Add(v, u, w);
    
    Init(1, 0);
    scanf("%d", & m);
    while (m--) {
        scanf("%d", & k);
        lep(i, 1, k) scanf("%d", h + i);
        Build(), Solve(1);
        printf("%lld\n", f[1]);
        Clear();
    }
    return 0;
}

[GZOI2017] 共享单车

Link 。没有简化题意，自己读。

点击查看

Dijstra 记录方案成一棵树，剩下的部分虚树后树上 \(DP\) 。和上一题类似。
注意题目中只能选择标记点间的全部路径截断。
注意题目中只需考虑被标记的投放区域。
注意题目中要求路径长度相同的取上一个节点编号最小的方案。


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)

typedef long long ll;
const int _ = 5e4 + 7;
const int inf = 2e9;

struct Edge { int v, n, w; }e[_ << 2]; int cnte = 1, H[_]; bool vis[_ << 2];
int n, m, rt, q, cnt[_]; ll dp[_];
int h[_], k, stk[_], Top;
int fa[_], top[_], sz[_], dep[_], son[_], dfn[_], idx, c[_]; bool col[_];
std::vector <int> g[_];
struct Node {
    ll d; int f, v;
    Node(ll _d, int _f, int _v) { d = _d, f = _f, v = _v; }
    friend bool operator > (Node x, Node y) {
        return x.d == y.d ? e[x.f ^ 1].v > e[y.f ^ 1].v : x.d > y.d;
    }
};
ll dis[_]; bool cur[_];

void Add(int u, int v, int w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void Dfs1(int u, int f) {
    sz[u] = 1, dep[u] = dep[fa[u] = f] + 1;
    ep(i, u, v) if (vis[i]) {
        Dfs1(v, u), sz[u] += sz[v];
        if (sz[v] > sz[son[u]]) son[u] = v;
    }
}
void Dfs2(int u, int tp) {
    top[u] = tp, dfn[u] = ++idx;
    if (!son[u]) return;
    Dfs2(son[u], tp);
    ep(i, u, v) if (vis[i] and v != son[u]) Dfs2(v, v);
}
int LCA(int x, int y) {
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
        x = fa[top[x]];
    }
    return dep[x] < dep[y] ? x : y;
}
void Build() {
    std::sort(h + 1, h + 1 + k, [](int x, int y) { return dfn[x] < dfn[y]; });
    stk[Top = 1] = rt, g[rt].clear();
    lep(i, 1, k) if (h[i] != rt) {
        int l = LCA(h[i], stk[Top]);
        if (l != stk[Top]) {
            while (dep[stk[Top - 1]] > dep[l]) g[stk[Top - 1]].push_back(stk[Top]), --Top;
            if (stk[Top - 1] == l) g[l].push_back(stk[Top--]);
            else g[l].clear(), g[l].push_back(stk[Top]), stk[Top] = l;
        }
        stk[++Top] = h[i], g[h[i]].clear();
    }
    lep(i, 1, Top - 1) g[stk[i]].push_back(stk[i + 1]);
}
void Dijstra(int s) { std::priority_queue <Node, std::vector<Node>, std::greater<Node> > d;
    lep(i, 1, n) dis[i] = inf;
    dis[s] = 0; d.push(Node(0, 0, s));
    while (!d.empty()) {
        int u = d.top().v, f = d.top().f; d.pop();
        if (cur[u]) continue; cur[u] = true, vis[f] = true;
        ep(i, u, v) if (dis[v] >= dis[u] + e[i].w)
            dis[v] = dis[u] + e[i].w, d.push(Node(dis[v], i, v));
    }
}
inline ll Len(int u, int v) { return dis[v] - dis[u]; }
void Solve(int u) {
    dp[u] = 0;
    for (int v : g[u]) {
        Solve(v);
        if (col[v]) dp[u] += Len(u, v);
        else dp[u] += std::min(Len(u, v), dp[v]);
    }
}

int main() {
    scanf("%d%d%d%d", & n, & m, & rt, & q); int u, v, w;
    lep(i, 1, m) scanf("%d%d%d", & u, & v, & w),
        Add(u, v, w), Add(v, u, w);
    Dijstra(rt), Dfs1(rt, 0), Dfs2(rt, rt);
    
    int op;
    while (q--) {
        scanf("%d%d", & op, & k);
        lep(i, 1, k) scanf("%d", h + i);
        if (!op)
            lep(i, 1, k) col[h[i]] = !col[h[i]];
        else {
            Build(), Solve(rt);
            printf("%lld\n", !dp[rt] ? -1 : dp[rt]);
        }
    }
    return 0;
}

[HEOI2014] 大工程

给一棵树。
在 \(2\) 个节点 \(a,b\) 之间连边需要的代价为树上 \(a,b\) 的最短路径的长度。
对于每次询问，选中 \(k\) 个点，然后在它们两两之间新建 \(\dbinom{k}{2}\) 条边。
求：

这些新通道的代价和。

这些新通道中代价最小的是多少。

这些新通道中代价最大的是多少。

点击查看

建完虚树后 \(DP\) 。
第一类询问，考虑每条边被算了多少次。
第二三类询问，维护以当前节点为深度最小节点的最长/次长/最短/次短链，更新答案。


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

typedef long long ll;
const int _ = 2e6 + 7;
const int inf = 1e9;

int n, q, k, h[_], dfn[_], idx;
int dep[_], stk[_], top, fa[_][21], siz[_];
int mn[_][2], mx[_][2], ans2(inf), ans3; ll ans1;
std::vector <int> e[_], g[_]; bool vis[_];

void Init(int u, int f) {
    dfn[u] = ++idx, dep[u] = dep[fa[u][0] = f] + 1;
    lep(i, 1, 20) fa[u][i] = fa[fa[u][i - 1]][i - 1];
    for (int v : e[u]) if (v != f) Init(v, u);
}
int LCA(int x, int y) {
    if (dep[x] < dep[y]) std::swap(x, y);
    rep(i, 20, 0) if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
    if (x == y) return x;
    rep(i, 20, 0) if (fa[x][i] != fa[y][i])
        x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}
void Build() {
    stk[top = 1] = 1, g[1].clear();
    std::sort(h + 1, h + 1 + k, [](int x, int y) { return dfn[x] < dfn[y]; });
    lep(i, 1, k) { vis[h[i]] = true;
        if (h[i] == 1) continue;
        int lca = LCA(h[i], stk[top]);
        if (lca != stk[top]) {
            while (dfn[stk[top - 1]] > dfn[lca])
                g[stk[top - 1]].push_back(stk[top]), --top;
            if (stk[top - 1] != lca)
                g[lca].clear(), g[lca].push_back(stk[top]), stk[top] = lca;
            else g[lca].push_back(stk[top--]);
        }
        g[h[i]].clear(), stk[++top] = h[i];
    }
    lep(i, 1, top - 1) g[stk[i]].push_back(stk[i + 1]);
}
void Solve(int u) {
    siz[u] = vis[u];
    mn[u][0] = mn[u][1] = mx[u][0] = mx[u][1] = 0;
    for (int v : g[u]) {
        Solve(v); int w = dep[v] - dep[u];
        siz[u] += siz[v];
        ans1 += 1ll * siz[v] * (k - siz[v]) * w;
        if (vis[v]) {
            if (!mn[u][0] or mn[u][0] >= w) mn[u][1] = mn[u][0], mn[u][0] = w;
            else if (!mn[u][1] or mn[u][1] > w) mn[u][1] = w;
        }
        else {
            if (!mn[u][0] or mn[u][0] >= w + mn[v][0]) mn[u][1] = mn[u][0], mn[u][0] = w + mn[v][0];
            else if (!mn[u][1] or mn[u][1] > w + mn[v][0]) mn[u][1] = w + mn[v][0];
        }
        if (w + mx[v][0] >= mx[u][0]) mx[u][1] = mx[u][0], mx[u][0] = w + mx[v][0];
        else if (w + mx[v][0] > mx[u][1]) mx[u][1] = w + mx[v][0];
    }
    
    if (vis[u] and mn[u][0])
        ans2 = std::min(ans2, mn[u][0]), ans3 = std::max(ans3, mx[u][0]);
    if (mn[u][1]) ans2 = std::min(ans2, mn[u][0] + mn[u][1]);
    if (mx[u][1]) ans3 = std::max(ans3, mx[u][0] + mx[u][1]);
}
void Clear() { lep(i, 1, k) vis[h[i]] = false; ans1 = ans3 = 0, ans2 = inf; }

int main() {
    scanf("%d", & n); int u, v;
    lep(i, 1, n - 1) scanf("%d%d", & u, & v),
        e[u].push_back(v), e[v].push_back(u);
    Init(1, 0);
    
    scanf("%d", & q);
    while (q--) {
        scanf("%d", & k);
        lep(i, 1, k) scanf("%d", h + i);
        Build(), Solve(1);
        printf("%lld %d %d\n", ans1, ans2, ans3);
        Clear();
    }
    return 0;
}

[HNOI2014] 世界树

世界树的形态可以用一个数学模型来描述：世界树中有 \(n\) 个种族，种族的编号分别从 \(1\) 到 \(n\)，分别生活在编号为 \(1\) 到 \(n\) 的聚居地上，种族的编号与其聚居地的编号相同。
第 \(i\) 年，世界树的国王需要授权 \(m_i\) 个种族的聚居地为临时议事处。对于某个种族 \(x\)（\(x\) 为种族的编号），如果距离该种族最近的临时议事处为 \(y\)（\(y\) 为议事处所在聚居地的编号），则种族 \(x\) 将接受 \(y\) 议事处的管辖（如果有多个临时议事处到该聚居地的距离一样，则 \(y\) 为其中编号最小的临时议事处）。
现在国王想知道，在 \(q\) 年的时间里，每一年完成授权后，当年每个临时议事处将会管理多少个种族（议事处所在的聚居地也将接受该议事处管理）。

点击查看

如图

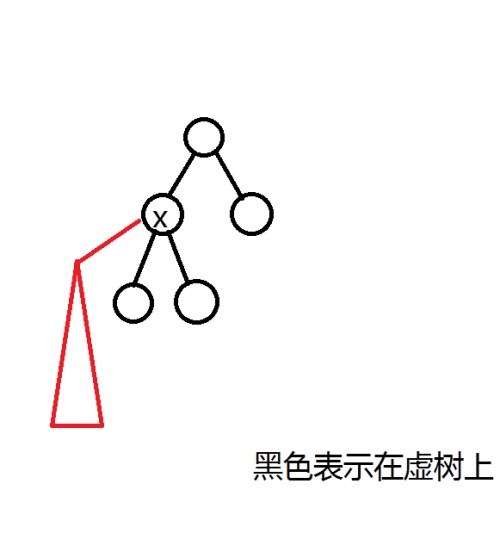
\(x\) 红色部分的子树的归属就是 \(x\) 的归属，所以完全可以把这部分变成 \(x\) 的点权。
然后两遍 \(Dfs\) 处理虚树上点的贡献，一遍考虑儿子对父亲，一遍考虑父亲对儿子。
最后还有虚树两点之间原树上点的贡献。

如图

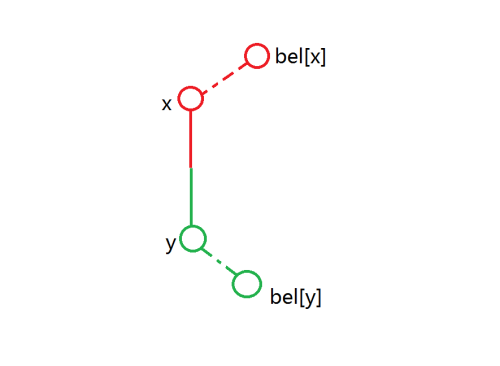
二分分界点，分界点以上的和 \(x\) 同样的归属，以下的和 \(y\) 同样的归属。


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

typedef long long ll;
const int _ = 3e5 + 7;

int n, q, k, h[_], p[_], stk[_], top, dfn[_], idx;
int fa[_][21], dep[_], siz[_], val[_], bel[_], dis[_], pr[_], ans[_];
std::vector <int> e[_], g[_]; bool un[_];

void Init(int u, int f) {
    dfn[u] = ++idx;siz[u] = 1, dep[u] = dep[fa[u][0] = f] + 1;
    lep(i, 1, 20) fa[u][i] = fa[fa[u][i - 1]][i - 1];
    for (int v : e[u]) if (v != f) {
        Init(v, u), siz[u] += siz[v];
    }
}
int LCA(int x, int y) {
    if (dep[x] < dep[y]) std::swap(x, y);
    rep(i, 20, 0) if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
    if (x == y) return x;
    rep(i, 20, 0) if (fa[x][i] != fa[y][i])
        x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}
void Add(int x, int y) { int rt = y;
    g[x].push_back(y);
    rep(i, 20, 0) if (dep[fa[y][i]] > dep[x])
        y = fa[y][i];
    pr[rt] = y;
}
void Build() {
    std::sort(h + 1, h + 1 + k, [](int x, int y) { return dfn[x] < dfn[y]; });
    stk[top = 1] = 1, g[1].clear();
    lep(i, 1, k) if (h[i] != 1) { un[h[i]] = true;
        int l = LCA(stk[top], h[i]);
        if (l != stk[top]) {
            while (dep[l] < dep[stk[top - 1]])
                Add(stk[top - 1], stk[top]), --top;
            if (l != stk[top - 1])
                g[l].clear(), Add(l, stk[top]), stk[top] = l;
            else Add(l, stk[top--]);
        }
        stk[++top] = h[i], g[h[i]].clear();
    } else un[1] = true;
    lep(i, 1, top - 1) Add(stk[i], stk[i + 1]);
}
int Len(int u, int v) { return dep[v] - dep[u]; }
void Dfs1(int u) {
    if (un[u]) bel[u] = u, dis[u] = 0;
    else bel[u] = 0, dis[u] = n;
    val[u] = siz[u];
    for (int v : g[u]) {
        Dfs1(v); val[u] -= siz[pr[v]];
        if (dis[v] + Len(u, v) < dis[u] or 
            (dis[v] + Len(u, v) == dis[u] and bel[v] < bel[u]))
            bel[u] = bel[v], dis[u] = dis[v] + Len(u, v);
    }
}
void Dfs2(int u) {
    for (int v : g[u]) {
        if (dis[u] + Len(u, v) < dis[v] or
            (dis[u] + Len(u, v) == dis[v] and bel[u] < bel[v]))
            bel[v] = bel[u], dis[v] = dis[u] + Len(u, v);
        Dfs2(v);
    }
    ans[bel[u]] += val[u];
}
bool Cmp(int x, int y, int z) {
    int c = (Len(x, y) + dis[x]) - (Len(y, z) + dis[z]);
    if (c > 0 or (!c and bel[z] < bel[x])) return true;
    return false;
}
void Dfs3(int u) {
    for (int v : g[u]) {
        Dfs3(v);
        int t = v;
        rep(i, 20, 0)
            if (dep[fa[t][i]] >= dep[u] and 
                Cmp(u, fa[t][i], v)) t = fa[t][i];
        ans[bel[u]] += siz[pr[v]] - siz[t],
        ans[bel[v]] += siz[t] - siz[v];
    }
}

int main() {
    scanf("%d", & n); int u, v;
    lep(i, 1, n - 1) scanf("%d%d", & u, & v),
        e[u].push_back(v), e[v].push_back(u);
    
    Init(1, 0);
    
    scanf("%d", & q);
    while (q--) {
        scanf("%d", & k);
        lep(i, 1, k) scanf("%d", h + i), p[i] = h[i];
        Build(); Dfs1(1); Dfs2(1); Dfs3(1);
        
        lep(i, 1, k) printf("%d ", ans[p[i]]);
        puts("");
        
        lep(i, 1, k) ans[h[i]] = un[h[i]] = 0;
    }
    return 0;
}

Kingdom and its Cities

一个王国有 \(n\) 座城市，城市之间由 \(n-1\) 条道路相连，形成一个树结构，国王决定将一些城市设为重要城市。
这个国家有的时候会遭受外敌入侵，重要城市由于加强了防护，一定不会被占领。而非重要城市一旦被占领，这座城市就不能通行。
国王定了若干选择重要城市的计划，他想知道，对于每个计划，外敌至少要占领多少个非重要城市，才会导致重要城市之间两两不连通。如果外敌无论如何都不可能导致这种局面，输出 \(-1\) 。

点击查看

在分叉处和祖先后代中间分讨即可，无需 \(DP\) 。
具体地，记录节点 \(u\) 有多少个子树内有关键点，再根据节点本身状态分讨。
如果没有必要现在占领，就继承状态等着之后再决定。
注意判无解必须在继承状态之前。


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

typedef long long ll;
const int _ = 1e5 + 7;

int n, q, fa[_][21], dep[_], k, h[_], res;
int stk[_], top, dfn[_], idx; bool vis[_];
std::vector <int> e[_], g[_];

void Init(int u, int f) {
    dfn[u] = ++idx, dep[u] = dep[fa[u][0] = f] + 1;
    lep(i, 1, 20) fa[u][i] = fa[fa[u][i - 1]][i - 1];
    for (int v : e[u]) if (v != f) {
        Init(v, u);
    }
}
int LCA(int x, int y) {
    if (dep[x] < dep[y]) std::swap(x, y);
    rep(i, 20, 0) if (dep[fa[x][i]] >= dep[y])
        x = fa[x][i];
    if (x == y) return x;
    rep(i, 20, 0) if (fa[x][i] != fa[y][i])
        x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}
void Build() {
    std::sort(h + 1, h + 1 + k, [](int x, int y) { return dfn[x] < dfn[y]; });
    stk[top = 1] = 1, g[1].clear();
    lep(i, 1, k) if (h[i] != 1) {
        int l = LCA(stk[top], h[i]);
        if (l != stk[top]) {
            while (dep[stk[top - 1]] > dep[l])
                g[stk[top - 1]].push_back(stk[top]), --top;
            if (stk[top - 1] != l)
                g[l].clear(), g[l].push_back(stk[top]), stk[top] = l;
            else g[l].push_back(stk[top--]);
        }
        stk[++top] = h[i], g[h[i]].clear();
    }
    lep(i, 1, top - 1) g[stk[i]].push_back(stk[i + 1]);
    lep(i, 1, k) vis[h[i]] = true;
}
void Solve(int u) {
    int son = 0;
    for (int v : g[u]) {
        if (vis[v] and vis[u] and dep[v] - dep[u] == 1)
            { res = -1; return; }
        Solve(v);
        if (res == -1) return;
        if (vis[v]) ++son;
    }
    if (!vis[u]) {
        if (son > 1) ++res;
        else if (son) vis[u] = true;
    }
    else res += son;
}
void Clear(int u) {
    vis[u] = false; res = 0;
    for (int v : g[u]) Clear(v);
}

int main() {
    scanf("%d", & n); int u, v;
    lep(i, 1, n - 1) scanf("%d%d", & u, & v),
        e[u].push_back(v), e[v].push_back(u);
    Init(1, 0);
    
    scanf("%d", & q);
    while (q--) {
        scanf("%d", & k);
        lep(i, 1, k) scanf("%d", h + i);
        Build();
        Solve(1);
        printf("%d\n", res); Clear(1);
    }
    return 0;
}

[JRKSJ R4] Salieri

给出 \(n\) 个字符串 \(s_i\)，每个字符串有一个权值 \(v_i\)。\(m\) 次询问每次给出一个字符串 \(S\) 和一个常数 \(k\)。设 \(cnt_i\) 为 \(s_i\) 在 \(S\) 中的出现次数，求 \(cnt_i\times v_i\) 第 \(k\) 大的值。

点击查看

匹配考虑对 \(s_i\) 建 \(ACM\) 。
如果暴力算出每个串的权值，复杂度是无法接受的。

求第 \(k\) 大，经典 \(trick\) 进行二分。
现在我们需要处理权值大于等于 \(x\) 的串有几个。
同时考虑上述暴力，发现 \(AC\) 自动机上存在子树求和操作。
并且，只有每个匹配点处有贡献，而不同匹配点间路径上的累和结果 \(siz\) 相同，提示我们使用虚树。
对所有匹配点建出虚树后，接下来我们需要处理一条祖孙链上有多少个结尾节点所代表的串的权值与 \(siz\) 相乘大于等于 \(x\) 。
即满足 \(siz\times v \geq x\) 的 \(v\) 的个数，移项得 \(v \geq \lceil \frac{x}{siz} \rceil\) 。
主席树即可。


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

const int _ = 5e5 + 7;
const int inf = 1010;

int n, m, q, x, k, ch[_ << 2][4], idx = 1, dfn[_ << 2], cnt;
int h[_], stk[_], dep[_ << 2], top, fa[_ << 2][20], sz[_ << 2];
int tot, ls[_ << 3], rs[_ << 3], sum[_ << 3], rt[_ << 2];
char s[_];
std::vector <int> g[_], val[_];

void Modify(int k, int l, int r, int u, int& p) {
    p = ++tot, sum[p] = sum[u] + 1, ls[p] = ls[u], rs[p] = rs[u];
    if (l == r) return; int mid = (l + r) >> 1;
    if (k <= mid) Modify(k, l, mid, ls[u], ls[p]);
    else Modify(k, mid + 1, r, rs[u], rs[p]);
}
int Query(int l, int r, int d, int x, int y) {
    if (!y or l > r) return 0;
    if (l >= d) return sum[y] - sum[x]; int mid = (l + r) >> 1, res = 0;
    res = Query(mid + 1, r, d, rs[x], rs[y]);
    if (d <= mid) res += Query(l, mid, d, ls[x], ls[y]);
    return res;
}

int Insert(char s[]) {
    int len = std::strlen(s + 1), nw = 1;
    lep(i, 1, len) { int k = s[i] - 'a';
        if (!ch[nw][k]) ch[nw][k] = ++idx;
        nw = ch[nw][k];
    }
    return nw;
}
void Build() { std::queue <int> d;
    lep(k, 0, 3) ch[0][k] = 1; d.push(1);
    while (!d.empty()) {
        int u = d.front(); d.pop();
        lep(k, 0, 3) if (ch[u][k]) h[ch[u][k]] = ch[h[u]][k], d.push(ch[u][k]);
        else ch[u][k] = ch[h[u]][k];
        g[h[u]].push_back(u);
    }
}
void Gets(char s[]) {
    int len = std::strlen(s + 1), nw = 1;
    lep(i, 1, len) nw = ch[nw][s[i] - 'a'], ++sz[nw], h[i] = nw;
    m = len;
}

void Init(int u, int f) {
    rt[u] = rt[f];
    for (int k : val[u]) Modify(k, 1, inf, rt[u], rt[u]);
    dfn[u] = ++cnt, dep[u] = dep[fa[u][0] = f] + 1;
    lep(k, 1, 18) fa[u][k] = fa[fa[u][k - 1]][k - 1];
    for (int v : g[u]) Init(v, u);
}
int LCA(int x, int y) {
    if (dep[x] < dep[y]) std::swap(x, y);
    rep(k, 18, 0) if (dep[fa[x][k]] >= dep[y]) x = fa[x][k];
    if (x == y) return x;
    rep(k, 18, 0) if (fa[x][k] != fa[y][k])
        x = fa[x][k], y = fa[y][k];
    return fa[x][0];
}
void BldVir() {
    std::sort(h + 1, h + 1 + m, [](int x, int y) { return dfn[x] < dfn[y]; });
    stk[top = 1] = 1, g[1].clear();
    lep(i, 1, m) if (h[i] > 1 and h[i] != h[i - 1]) {
        int l = LCA(stk[top], h[i]);
        if (l != stk[top]) {
            while (dep[stk[top - 1]] > dep[l]) g[stk[top - 1]].push_back(stk[top]), --top;
            if (stk[top - 1] == l) g[l].push_back(stk[top--]);
            else g[l].clear(), g[l].push_back(stk[top]), stk[top] = l;
        }
        g[h[i]].clear(), stk[++top] = h[i];
    }
    lep(i, 1, top - 1) g[stk[i]].push_back(stk[i + 1]);
}
void Cls(int u) { sz[u] = 0;
    for (int v : g[u]) Cls(v);
    g[u].clear();
}
void DFS(int u) { for (int v : g[u]) DFS(v), sz[u] += sz[v]; }

int Check(int u, int f, int x) {
    int res = 0, nw;
    for (int v : g[u]) res += Check(v, u, x);
    if (u != 1) {
        nw = (x + sz[u] - 1) / sz[u];
        if (nw <= inf) res += Query(1, inf, nw, rt[f], rt[u]);
    }
    return res;
}

int main() {
    scanf("%d%d", & n, & q);
    lep(i, 1, n) scanf("%s %d", s + 1, & x), val[Insert(s)].push_back(x);
    Build(); Init(1, 0);
    
    while (q--) {
        scanf("%s %d", s + 1, & k);
        Gets(s); BldVir(); DFS(1);
        
        int l = 0, r = 1e9;
        while (l < r) { int mid = (l + r + 1) >> 1;
            if (Check(1, 0, mid) >= k) l = mid;
            else r = mid - 1;
        }
        printf("%d\n", l); Cls(1);
    }
    return 0;
}

I-不散的宴会

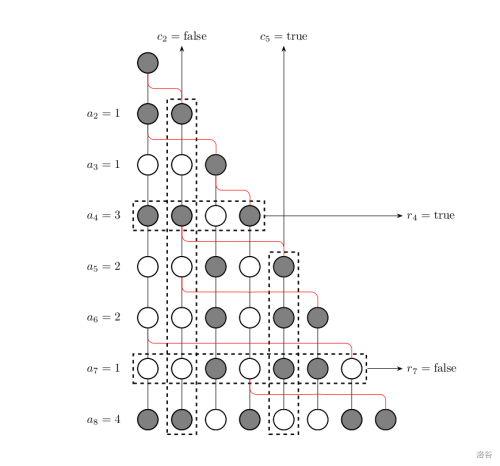
学生社团可以被看作一个排列成等腰直角三角形的节点阵列。该节点阵列共有 \(n\) 行，第 \(i\) 行共有 \(i\) 个节点。我们将第 \(i\) 行第 \(j\) 列的节点，标号为 \((i,j)\)。

这些节点具有权值。具体而言，节点 \((i,j)\) 的权值为 \(r_i\oplus c_j\)，其中 \(r\) 和 \(c\) 是给定的 \(01\) 序列，\(\oplus\) 是二进制异或操作。

这些节点有边相连。具体而言，对于 \(1\le i< n\)，\(1\le j\le i\)，会有一条边连接 \((i,j)\) 和 \((i+1,j)\)。此外，对于 \(2\le i\le n\)，还会有边连接 \((i,i)\) 和 \((i-1,a_i)\)。其中 \(a\) 是给定的序列。

现在你需要从这些节点中，选出一些节点，使得这些节点间两两不存在边相连，最大化选出来的节点的权值之和。

点击查看

将第一层与第 \(n\) 层的所有点，中间所有被下一层末端指向的节点作为关键点建虚树。
然后是经典的树形 \(DP\) 。
转移时我们需要处理两个祖孙关键点之间非关键点的贡献。
容易发现这样的关键点之间的路径（不包括端点）纵坐标都相同，即这是一个 \(01\) 序列区间最大独立集问题。
预处理出 \(r_i\) 以及 \(\neg\) \(r_i\) 的 \(p_i\) 与 \(h_i\) ，分别表示 \(i\) 这个位置所在的 \(1\) 的极长段的末尾位置和前缀答案，即可做到 \(O(1)\) 查询。
关于建立虚树，从上往下处理的同时，记录 \(col_y\) ，表示如果 \(y\) 列出现了新的节点应作为谁的儿子。


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)

typedef long long ll;
typedef std::pair<int, int> PII;
const int _ = 3e6 + 7;

int n, r[_], c[_], a[_]; ll f[_][2];
int h[_][2], p[_][2], col[_], idx;
PII pos[_]; std::vector <int> e[_];

void Init() {
    rep(i, n, 1) {
        if (i < n and r[i] and r[i + 1]) p[i][0] = p[i + 1][0];
        else p[i][0] = i;
        if (i < n and !r[i] and !r[i + 1]) p[i][1] = p[i + 1][1];
        else p[i][1] = i;
    }
    int cnt0 = 0, lst0 = 0, cnt1 = 0, lst1 = 0;
    lep(i, 1, n) {
        if (r[i]) ++cnt0, h[i][0] = h[lst0][0] + ((cnt0 + 1) >> 1), cnt1 = 0, lst1 = i, h[i][1] = h[i - 1][1];
        else cnt0 = 0, lst0 = i, h[i][0] = h[i - 1][0], ++cnt1, h[i][1] = h[lst1][1] + ((cnt1 + 1) >> 1);
    }
}
int Query(int L, int R, int k) { if (L > R) return 0; int pl = std::min(p[L][k], R);
    return h[R][k] - h[pl][k] + ((pl - L + 1 + (r[L] ^ k)) >> 1);  }
void Build() {
    lep(i, 1, n - 1) {
        int y = a[i + 1]; pos[++idx] = { i, y };
        if (col[y]) e[col[y]].push_back(idx); col[y] = idx;
        col[y] = col[i + 1] = idx;
    }
    lep(y, 1, n) e[col[y]].push_back(++idx), pos[idx] = { n, y };
}
void Solve(int u) {
    f[u][1] = r[pos[u].first] ^ c[pos[u].second];
    for (int v : e[u]) {
        Solve(v);
        int x = pos[u].first + 1, y = pos[v].first - 1, p = pos[v].second;
        if (x == y + 1)
            f[u][0] += std::max(f[v][0], f[v][1]), f[u][1] += f[v][0];
        else {
            f[u][0] += std::max(Query(x, y, c[p]) + f[v][0], Query(x, y - 1, c[p]) + std::max(f[v][0], f[v][1])),
            f[u][1] += std::max(Query(x + 1, y, c[p]) + f[v][0], Query(x + 1, y - 1, c[p]) + std::max(f[v][0], f[v][1]));
        }
    }
}

int main() {
    scanf("%d", & n);
    lep(i, 1, n) scanf("%d", r + i);
    lep(i, 1, n) scanf("%d", c + i);
    lep(i, 2, n) scanf("%d", a + i);
    Init(), Build(), Solve(1);
    printf("%lld\n", std::max(f[1][0], f[1][1]));
    return 0;
}

Bear and Chemistry

给定一张初始无向图，处理 \(q\) 次询问。
每次询问给定一个点集 \(V\) 和一个边集 \(E\)，求将 \(E\) 中的边加入初始无向图之后，\(V\) 中任意两个点 \(x\) , \(y\) 是否都能在每条边至多经过一次的情况下从 \(x\) 到 \(y\) 再回到 \(x\)。强制在线。

点击查看

将原图根据边双缩成一棵树。
每次询问将点集中的点和边集的端点建成虚树，再将边集加入后跑边双，点集中的点属于一个边双即 \(YES\) 。


#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)

typedef long long ll;
const int _ = 1e6 + 7;
const int V = 25;

struct node { int v, n; }e[_]; int H[_], cnte = 1; bool vis[_], un[_];
int n, m, q, dfn[_], low[_], idx, stk[_], top, scc, bel[_], rmb[_], DFN[_], u[_], v[_];
int fa[_][V + 1], dep[_], id[_], rt[_]; int R;
std::vector <int> g[_], Ques;

int rotate(int element)
{
   element=(element+R)%n;
   if (element==0) element=n;
   return element;
}
void Add(int u, int v) { e[++cnte] = { v, H[u] }, vis[H[u] = cnte] = false; }
void Tarjan(int u) {
    dfn[u] = low[u] = ++idx, stk[++top] = u;
    ep(i, u, v) {
        if (vis[i]) continue; vis[i ^ 1] = true;
        if (!dfn[v]) Tarjan(v), low[u] = std::min(low[u], low[v]);
        else low[u] = std::min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) { ++scc;
        while (stk[top] != u) bel[stk[top--]] = scc;
        bel[stk[top--]] = scc;
    }
}
void Init(int u, int f, int p) {
    if (dep[u]) return; rt[u] = p;
    DFN[u] = ++idx, dep[u] = dep[fa[u][0] = f] + 1;
    lep(i, 1, V) fa[u][i] = fa[fa[u][i - 1]][i - 1];
    for (int v : g[u]) if (v != f) Init(v, u, p);
}
int LCA(int x, int y) {
    if (dep[x] < dep[y]) std::swap(x, y);
    rep(i, V, 0) if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
    if (x == y) return x;
    rep(i, V, 0) if (fa[x][i] != fa[y][i])
        x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}
void Upd(int u) { dfn[u] = H[u] = 0, un[u] = true; } 
void ADD(int u, int v) { Add(u, v), Add(v, u); }
void Build(int l, int r) {
    std::sort(id + l, id + r + 1, [](int x, int y) { return DFN[x] < DFN[y]; });
    int R = rt[id[l]];
    stk[top = 1] = R, Upd(R);
    lep(j, l, r) { int i = id[j];
        if (i == R) continue;
        int l = LCA(i, stk[top]);
        if (l != stk[top]) {
            while (dep[stk[top - 1]] > dep[l]) ADD(stk[top - 1], stk[top]), --top;
            if (stk[top - 1] == l) ADD(stk[top - 1], stk[top]), --top;
            else Upd(l), ADD(l, stk[top]), stk[top] = l;
        }
        stk[++top] = i, Upd(i);
    }
    lep(i, 1, top - 1) ADD(stk[i], stk[i + 1]);
}
void Cls(int u) { if (!un[u]) return; un[u] = false;
    ep(i, u, v) if (un[v]) Cls(v);
}

int main() {
    scanf("%d%d%d", & n, & m, & q);
    lep(i, 1, m) scanf("%d%d", u + i, v + i), ADD(u[i], v[i]);
    lep(i, 1, n) if (!dfn[i]) idx = top = 0, Tarjan(i);
    lep(i, 2, cnte) if (bel[e[i].v] != bel[e[i ^ 1].v]) g[bel[e[i].v]].push_back(bel[e[i ^ 1].v]);
    lep(i, 1, n) rmb[i] = bel[i]; idx = 0;
    lep(i, 1, scc) if (!DFN[i]) Init(i, 0, i);
    
    int N, M;
    lep(Q, 1, q) {
        scanf("%d%d", & N, & M);
        lep(i, 1, N) scanf("%d", id + i), id[i] = rmb[rotate(id[i])];
        std::sort(id + 1, id + 1 + N), N = std::unique(id + 1, id + 1 + N) - id - 1;
        Ques.clear(); lep(i, 1, N) Ques.push_back(id[i]); int tot = 0;
        lep(i, 1, M) {
            scanf("%d%d", u + i, v + i); u[i] = rmb[rotate(u[i])], v[i] = rmb[rotate(v[i])];
            if (u[i] == v[i]) continue;
            id[N + (++tot)] = u[i], id[N + (++tot)] = v[i];
        }
        std::sort(id + 1, id + 1 + N + tot), N = std::unique(id + 1, id + 1 + N + tot) - id - 1;
        int l = 1, r = 0; cnte = 1;
        while (l <= N) {
            while (rt[id[r + 1]] == rt[id[l]]) ++r;
            Build(l, r), l = r + 1;
        }
        lep(i, 1, M) if (u[i] != v[i]) ADD(u[i], v[i]);
        scc = 0;
        for (int k : Ques) if (!dfn[rt[k]]) idx = top = 0, Tarjan(rt[k]);
        l = 0, r = 1;
        for (int k : Ques) {
            if (!l) l = bel[k];
            else if (l != bel[k]) { r = 0; break; }
        }
        for (int k : Ques) Cls(rt[k]);
        if (r) R = (R + Q) % n, puts("YES");
        else puts("NO");
    }
    return 0;
}

posted @ 2025-04-29 15:11 qkhm 阅读(92) 评论(3) 收藏举报

刷新页面返回顶部

Loading

幽光闪烁

算法笔记 - 虚树

引入

[SDOI2011] 消耗战

虚树概述

构建

例题

[SDOI2011] 消耗战

[GZOI2017] 共享单车

[HEOI2014] 大工程

[HNOI2014] 世界树

Kingdom and its Cities

[JRKSJ R4] Salieri

I-不散的宴会

Bear and Chemistry

公告