算法笔记 - 树分治
点分治
概述
点分治是一类方法,用于处理树上任意两点之间路径相关问题。
一般采取分类的思想,每次选定一个节点,并强制所处理路径全部经过此节点,处理完后删除,在递归处理形成的森林,且不同的树间不相互影响。
实现细节
首先,每次删除的点决定了森林的划分形式,将点之间分层,形成了一个新的树形结构。
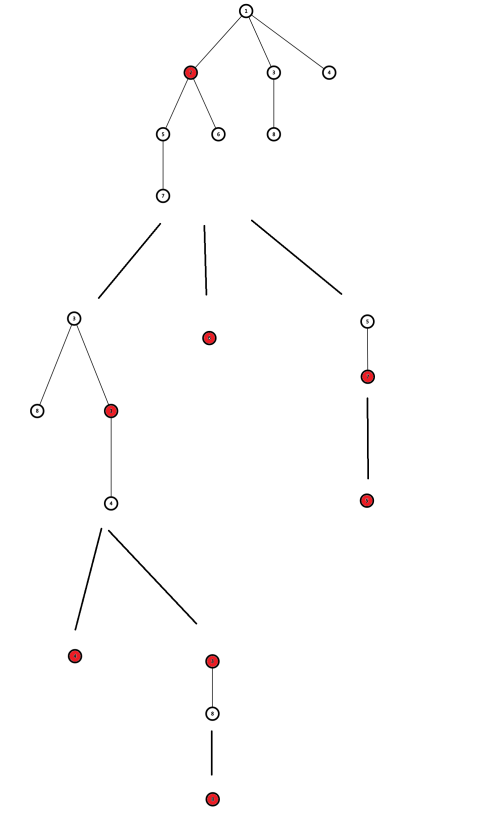
而每一层都会对 \(O(n)\) 量级的每一个点进行处理,为了复杂度正确,我们希望树的深度尽可能小,即每一层都尽可能均分。
\(\text{那我们应该删除什么样的点呢?}\) 直觉告诉我们应该删除最大子树最小的那个点,即 \(\textbf{树的重心}\)。
根据重心的性质,每一次删除重心后剩下的子树最大不超过原大小的一半,所以树高为 \(\log n\) 级别。
时间复杂度一般多带一个 \(\log\) ,例如统计一个重心为 \(O(n\log n)\) ,则总复杂度为 \(O(n\log^2 n)\) 。
而取重心代码如下:
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)
void GetRt(int u, int f, int total) { //total 是所在树的大小
sz[u] = 1, tmp[u] = 0;
ep(i, u, v) if (!vis[v] and v != f) {
GetRt(v, u, total); sz[u] += sz[v];
tmp[u] = std::max(tmp[u], sz[v]);
}
tmp[u] = std::max(tmp[u], total - sz[u]); // 别忘了父亲方向的子树
if (!rt or tmp[u] < tmp[rt]) rt = u; // 取最大子树最小的
}
递归处理函数如下:
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total);
vis[rt] = true, Calc(rt); //Calc(u) 处理经过 u 点的路径
ep(i, rt, v) if (!vis[v])
Solve(v, total - tmp[v]);
}
上述代码中,我们使用 total - tmp[v] 来获得新树的大小,具体的可以看图:
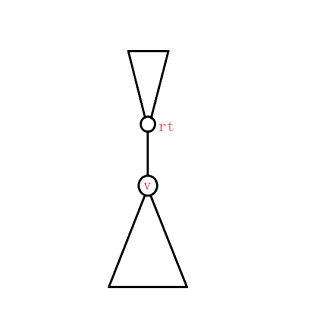
如果 \(v\) 的最大子树不在 \(rt\) 方向,那么重心应该是 \(v\) 而不是 \(rt\) 。
所以,真实的图一定是将上面的 \(v\) 和 \(rt\) 互换。上述式子是正确的。
例题
【模板】点分治 1
给定一棵有 n 个点的树,询问树上距离为 k 的点对是否存在。
点击查看
路径问题考虑拼接,对于另外一个端点,我们需要记录它的到根路径长度 \(dis\) ,以及属于哪棵子树 \(bel\) 。
对于每一个询问,双指针统计。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)
typedef long long ll;
const int _ = 1e4 + 7;
struct Edge { int v, n, w; }e[_ << 1]; int cnte = 1, H[_];
int n, m, q[_], rt, sz[_], tmp[_], k[_]; bool ans[_], vis[_];
int cnt[_], bel[_]; ll dis[_];
void Add(int u, int v, int w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
ep(i, u, v) if (!vis[v] and v != f) {
GetRt(v, u, total); sz[u] += sz[v];
tmp[u] = std::max(tmp[u], sz[v]);
}
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
void Dfs(int u, int f, int d, int rt) {
cnt[++*cnt] = u, dis[u] = dis[f] + d, bel[u] = rt;
ep(i, u, v) if (v != f and !vis[v]) Dfs(v, u, e[i].w, rt);
}
void Calc(int u) { cnt[*cnt = 1] = u, dis[u] = 0, bel[u] = 0;
ep(i, u, v) if (!vis[v]) Dfs(v, u, e[i].w, v);
std::sort(cnt + 1, cnt + 1 + *cnt, [](int x, int y)
{ return dis[x] < dis[y]; });
lep(i, 1, m) if (!ans[i]) {
int l = 1, r = *cnt;
while (l < r) {
if (dis[cnt[l]] + dis[cnt[r]] < k[i]) ++l;
else if (dis[cnt[l]] + dis[cnt[r]] > k[i]) --r;
else {
if (bel[cnt[l]] == bel[cnt[r]]) {
if (dis[cnt[l]] == dis[cnt[l + 1]]) ++l;
else --r;
}
else { ans[i] = true; break; }
}
}
}
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total);
vis[rt] = true, Calc(rt);
ep(i, rt, v) if (!vis[v])
Solve(v, total - tmp[v]);
}
int main() {
scanf("%d%d", & n, & m); int u, v, w;
lep(i, 1, n - 1) scanf("%d%d%d", & u, & v, & w),
Add(u, v, w), Add(v, u, w);
lep(i, 1, m) scanf("%d", k + i);
Solve(1, n);
lep(i, 1, m) puts(ans[i] ? "AYE" : "NAY");
return 0;
}
[IOI 2011] Race
给一棵树,每条边有权。求一条简单路径,权值和等于 k,且边的数量最小。
点击查看
类似上一道题,选择更不接近答案的一侧移动指针。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)
typedef long long ll;
const int _ = 2e5 + 7;
struct Edge { int v, n, w; }e[_ << 1]; int cnte = 1, H[_];
int n, rt, sz[_], tmp[_], k, ans; bool vis[_];
int cnt[_], bel[_], len[_]; ll dis[_];
void Add(int u, int v, int w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
ep(i, u, v) if (!vis[v] and v != f) {
GetRt(v, u, total); sz[u] += sz[v];
tmp[u] = std::max(tmp[u], sz[v]);
}
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
void Dfs(int u, int f, int d, int rt) {
cnt[++*cnt] = u, dis[u] = dis[f] + d, len[u] = len[f] + 1, bel[u] = rt;
ep(i, u, v) if (v != f and !vis[v]) Dfs(v, u, e[i].w, rt);
}
void Calc(int u) { cnt[*cnt = 1] = u, dis[u] = len[u] = bel[u] = 0;
ep(i, u, v) if (!vis[v]) Dfs(v, u, e[i].w, v);
std::sort(cnt + 1, cnt + 1 + *cnt, [](int x, int y)
{ return dis[x] == dis[y] ? len[x] < len[y] : dis[x] < dis[y]; });
int l = 1, r = *cnt;
while (l < r) {
if (dis[cnt[l]] + dis[cnt[r]] < k) ++l;
else if (dis[cnt[l]] + dis[cnt[r]] > k) --r;
else {
if (bel[cnt[l]] == bel[cnt[r]]) {
if (dis[cnt[r - 1]] == dis[cnt[r]]) --r;
else ++l;
}
else {
ans = std::min(ans, len[cnt[l]] + len[cnt[r]]);
if (dis[cnt[r - 1]] == dis[cnt[r]]) --r;
else ++l;
}
}
}
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total);
vis[rt] = true, Calc(rt);
ep(i, rt, v) if (!vis[v]) Solve(v, total - tmp[v]);
}
int main() {
scanf("%d%d", & n, & k); int u, v, w; ans = n * 2;
lep(i, 1, n - 1) scanf("%d%d%d", & u, & v, & w), ++u, ++v,
Add(u, v, w), Add(v, u, w);
Solve(1, n);
if (ans == n * 2) puts("-1");
else printf("%d\n", ans);
return 0;
}
Tree
给定一棵 n 个节点的树,每条边有边权,求出树上两点距离小于等于 k 的点对数量。
点击查看
容斥。
先不考虑路径两个端点不能在同一棵子树里,使用双指针或二分统计。
然后如图:
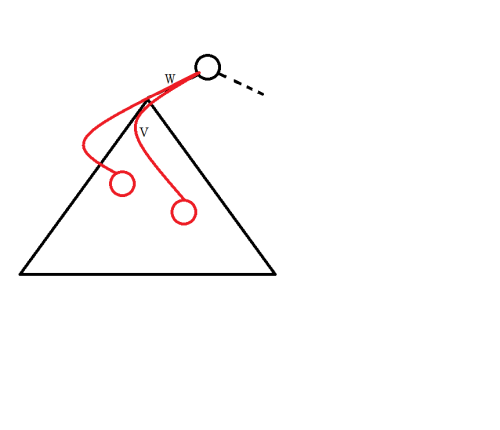
我们只需要用同样的方法在子树 \(v\) 中统计 \(\le k - 2 \times w\) 的个数再减掉就好了。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)
typedef long long ll;
const int _ = 4e4 + 7;
struct Edge { int v, n, w; }e[_ << 1]; int cnte = 1, H[_];
int n, m, rt, sz[_], tmp[_], k, ans; bool vis[_];
int cnt[_]; ll dis[_];
void Add(int u, int v, int w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
ep(i, u, v) if (!vis[v] and v != f) {
GetRt(v, u, total); sz[u] += sz[v];
tmp[u] = std::max(tmp[u], sz[v]);
}
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
void Dfs(int u, int f, int d) {
cnt[++*cnt] = u, dis[u] = dis[f] + d;
ep(i, u, v) if (v != f and !vis[v]) Dfs(v, u, e[i].w);
}
int Calc(int u, int d = 0) { cnt[*cnt = 1] = u, dis[u] = 0; int res = 0;
ep(i, u, v) if (!vis[v]) Dfs(v, u, e[i].w);
std::sort(cnt + 1, cnt + 1 + *cnt, [](int x, int y)
{ return dis[x] < dis[y]; });
int l = 1, r = *cnt;
while (l < r) {
while (l < r and dis[cnt[l]] + dis[cnt[r]] > k - d) --r;
res += r - l; ++l;
}
return res;
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total);
vis[rt] = true, ans += Calc(rt);
ep(i, rt, v) if (!vis[v])
ans -= Calc(v, 2 * e[i].w), Solve(v, total - tmp[v]);
}
int main() {
scanf("%d", & n); int u, v, w;
lep(i, 1, n - 1) scanf("%d%d%d", & u, & v, & w),
Add(u, v, w), Add(v, u, w);
scanf("%d", & k);
Solve(1, n);
printf("%d\n", ans);
return 0;
}
[国家集训队] 聪聪可可
满足 \(u\) 到 \(v\) 的路径边权和为 \(3\) 的倍数的点对 \((u, v)\) 计数。
点击查看
开 \(3\) 个桶分别记录对 \(3\) 取模为 \(0\) , \(1\) , \(2\) 的路径个数。
依次扫过每个儿子,考虑对之前所有儿子的贡献。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)
typedef long long ll;
const int _ = 2e4 + 7;
struct Edge { int v, n, w; }e[_ << 1]; int cnte = 1, H[_];
int n, m, rt, sz[_], tmp[_], ans, dis[3], cnt[3]; bool vis[_];
void Add(int u, int v, int w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
ep(i, u, v) if (!vis[v] and v != f) {
GetRt(v, u, total); sz[u] += sz[v];
tmp[u] = std::max(tmp[u], sz[v]);
}
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
void Dfs(int u, int f, int d) {
++cnt[d];
ep(i, u, v) if (!vis[v] and v != f)
Dfs(v, u, (d + e[i].w) % 3);
}
void Calc(int u) { dis[1] = dis[2] = 0; dis[0] = 1;
ep(i, u, v) if (!vis[v]) {
cnt[0] = cnt[1] = cnt[2] = 0;
Dfs(v, u, e[i].w);
ans += cnt[0] * dis[0] + cnt[1] * dis[2] + cnt[2] * dis[1];
dis[0] += cnt[0], dis[1] += cnt[1], dis[2] += cnt[2];
}
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total);
vis[rt] = true, Calc(rt);
ep(i, rt, v) if (!vis[v])
Solve(v, total - tmp[v]);
}
int main() {
scanf("%d", & n); int u, v, w;
lep(i, 1, n - 1) scanf("%d%d%d", & u, & v, & w), w %= 3,
Add(u, v, w), Add(v, u, w);
Solve(1, n);
ans = ans * 2 + n;
int m = n * n, g = std::__gcd(ans, m);
ans /= g, m /= g;
printf("%d/%d", ans, m);
return 0;
}
树上游戏
给一棵带颜色树,定义 \(s(i, j)\) 为 \(i\) 到 \(j\) 路径上的颜色种类数。
\(ans_i = \sum_j s(i, j)\), 求出所有的 \(ans_i\) 。
点击查看
路径贡献同样考虑点分治。
对于一个重心,处理出每条到根路径的答案。
考虑拼接时不同的路径会有重复,用 \(map\) 存下每种颜色的贡献。
对每种有贡献的颜色减去其他子树中这种颜色的贡献即可。
复杂度为 \(O(n\log^2 n)\) 。
\(Upd:\) 参照下一题代码不使用 \(map\) 而使用桶可以做到一个 \(\log\) 。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 1e5 + 7;
typedef long long ll;
int n, c[_]; ll ans[_];
int sz[_], tmp[_], rt, cnt[_], num, tot[_], res; bool vis[_]; int sum[_], All, delta;
std::vector <int> e[_];
std::map<int, int> S[_];
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
for (int v : e[u]) if (!vis[v] and v != f)
GetRt(v, u, total), sz[u] += sz[v], tmp[u] = std::max(tmp[u], sz[v]);
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
void Dfs1(int u, int f, int bel) {
sz[u] = 1;
if (!tot[c[u]]) ++res; ++tot[c[u]];
sum[bel] += res, All += res; ++cnt[bel], ++num;
for (int v : e[u]) if (!vis[v] and v != f)
Dfs1(v, u, bel), sz[u] += sz[v];
--tot[c[u]]; if (!tot[c[u]]) S[bel][c[u]] += sz[u], S[0][c[u]] += sz[u], --res;
}
void Dfs2(int u, int f, int bel) {
if (!tot[c[u]]) delta += (S[0][c[u]] - S[bel][c[u]]), ++res; ++tot[c[u]];
ans[u] += (All - sum[bel]) + (res - 1ll) * (num - cnt[bel]) - delta;
for (int v : e[u]) if (!vis[v] and v != f) Dfs2(v, u, bel);
--tot[c[u]]; if (!tot[c[u]]) delta -= (S[0][c[u]] - S[bel][c[u]]), --res;
}
void Calc(int u) {
S[0].clear(); int son = 0;
++tot[c[u]], ++res; All = num = 1;
for (int v : e[u]) if (!vis[v])
S[++son].clear(), cnt[son] = sum[son] = 0, Dfs1(v, u, son);
ans[u] += All, son = 0;
for (int v : e[u]) if (!vis[v]) delta = 0, Dfs2(v, u, ++son);
--res, --tot[c[u]];
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total), Calc(rt), vis[rt] = true;
for (int v : e[rt]) if (!vis[v]) Solve(v, total - tmp[v]);
}
int read() {
int x = 0; char c = getchar();
while (c < '0' or c > '9') c = getchar();
while (c >= '0' and c <= '9') x = x * 10 + c - '0', c = getchar();
return x;
}
int main() {
n = read();
lep(i, 1, n) c[i] = read(); int u, v;
lep(i, 2, n) u = read(), v = read(),
e[u].push_back(v), e[v].push_back(u);
Solve(1, n);
lep(i, 1, n) printf("%lld\n", ans[i]);
return 0;
}
Palindromes in a Tree
给你一棵 \(n\) 个节点的字母树。树上的一条路径是回文是指至少有一个对应字母的排列为回文。
对于每个顶点,输出通过它的回文路径的数量。
注意:从 \(u\) 到 \(v\) 的路径与从 \(v\) 到 \(u\) 的路径视为相同,只计数一次。
点击查看
题目的回文路径等价于最多有一个字符出现了奇数次,字符 $a\sim t $ , 总共 \(20\) 个字符,启示我们用状压。
具体的,存下两个状态的桶 \(S\) 和 \(T\), 分别表示整体与当前子树,用类似上题的方式统计。
统计方式是扫描字符集,枚举出现奇数次的字符。
计算贡献时需要使用子树求和累加,根节点处需要根据含义仔细推敲式子。
复杂度 \(O(\left | s \right | n\log n)\) 。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
typedef long long ll;
const int _ = 2e5 + 7;
int n; char s[_]; ll ans[_], sum[_], delta;
int sz[_], tmp[_], rt, S[_ << 4], T[_ << 4]; bool vis[_];
std::vector <int> e[_];
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
for (int v : e[u]) if (!vis[v] and v != f)
GetRt(v, u, total), sz[u] += sz[v], tmp[u] = std::max(tmp[u], sz[v]);
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
int Val(int Hsh) {
int res = 0;
rep(i, 19, 0) res += S[Hsh ^ (1 << i)] - T[Hsh ^ (1 << i)];
res += S[Hsh] - T[Hsh];
return res;
}
void Dfs1(int u, int f, int Hsh) {
Hsh ^= (1 << s[u] - 'a'), ++S[Hsh];
for (int v : e[u]) if (!vis[v] and v != f) Dfs1(v, u, Hsh);
}
void Dfs2(int u, int f, int Hsh) {
Hsh ^= (1 << s[u] - 'a'), ++T[Hsh];
for (int v : e[u]) if (!vis[v] and v != f) Dfs2(v, u, Hsh);
}
void Dfs3(int u, int f, int Hsh) {
Hsh ^= (1 << s[u] - 'a'), sum[u] = Val(Hsh);
for (int v : e[u]) if (!vis[v] and v != f) Dfs3(v, u, Hsh), sum[u] += sum[v];
ans[u] += sum[u];
}
void Cls(int u, int f, int Hsh, int* A) {
Hsh ^= (1 << s[u] - 'a'), --A[Hsh];
for (int v : e[u]) if (!vis[v] and v != f) Cls(v, u, Hsh, A);
}
void Calc(int u) { ll delta = 0;
++S[1 << s[u] - 'a'];
for (int v : e[u]) if (!vis[v]) Dfs1(v, u, 1 << s[u] - 'a');
for (int v : e[u]) if (!vis[v]) {
Dfs2(v, u, 1 << s[u] - 'a'), Dfs3(v, u, 0), delta += sum[v];
Cls(v, u, 1 << s[u] - 'a', T);
}
rep(i, 19, 0) delta += S[1 << i];
delta += S[0] - 1;
ans[u] += delta / 2 + 1;
for (int v : e[u]) if (!vis[v]) Cls(v, u, 1 << s[u] - 'a', S);
--S[1 << s[u] - 'a'];
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total), Calc(rt), vis[rt] = true;
for (int v : e[rt]) if (!vis[v]) Solve(v, total - tmp[v]);
}
int main() {
scanf("%d", & n); int u, v;
lep(i, 2, n) scanf("%d%d", & u, & v),
e[u].push_back(v), e[v].push_back(u);
scanf("%s", s + 1);
Solve(1, n);
lep(i, 1, n) printf("%lld ", ans[i]);
return 0;
}
树上的毒瘤
给一棵树,要求支持两种操作:
1 u v y: \(u\) 到 \(v\) 的路径上的颜色修改为 \(y\) 。
2 k h1 … hk: 给定一个大小为 \(k\) 的集合 \(S\),要求求出每个点的价值,定义点 \(i\) 的价值为 \(\sum_{j\in S} T(i, j)\) 。其中, \(T(i, j)\) 表示 \(i\) 到 \(j\) 的路径上的颜色段数。
点击查看
树剖维护颜色段数,套一棵线段树维护三元组 \((l, r, t)\) ,分别表示所维护区间的:左端点的颜色,右端点颜色,颜色段数量。
总询问规模启示我们使用虚树,点对之间的贡献又启示我们使用点分治。
考虑在虚树上点分治,我们每次处理跨过重心的点对之间的贡献。
拼接,令一条到根路径的权值 \(v_i\) 为其颜色段数.
若 \(i\) 、 \(j\) 是两个路径跨过重心的点,则 \(j\) 对 \(i\) 的贡献为 \(v_i + v_j - 1\) 。
好了,你会了,开始码吧。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 1e5 + 7;
typedef long long ll;
struct node {
int l, r, t, tag;
node(int _l = 0, int _r = 0, int _t = 0, int _tag = 0) { l = _l, r = _r, t = _t, tag = _tag; }
friend node operator + (const node& x, const node& y) {
if (x.t == 0) return y; if (y.t == 0) return x;
return node(x.l, y.r, x.t + y.t - (x.r == y.l));
}
friend void operator +=(node& x, const node& y) { x = x + y; }
friend node operator * (const node& x, const int& y) { return node(y, y, 1, y); }
friend void operator *=(node& x, const int& y) { x = x * y; }
node Swap() { std::swap(l, r); return *this; }
}tr[_ << 2];
int n, q, c[_], h[_], id[_], k, TOP, stk[_], Vit; bool un[_];
int dep[_], fa[_], top[_], son[_], sz[_], dfn[_], ud[_], idx;
int rt, tmp[_], cnt[_], tot; bool vis[_]; ll All, val[_], ans[_];
std::vector<int> e[_], g[_];
#define ls p << 1
#define rs p << 1 | 1
void PushUp(int p) { tr[p] = tr[ls] + tr[rs]; }
void PushDown(int p) { if (tr[p].tag) tr[ls] *= tr[p].tag, tr[rs] *= tr[p].tag, tr[p].tag = 0; }
void Build(int l, int r, int p) {
if (l == r) return tr[p] = node(c[ud[l]], c[ud[l]], 1), void(); int mid = (l + r) >> 1;
Build(l, mid, ls), Build(mid + 1, r, rs); PushUp(p);
}
void Modify(int l, int r, int s, int t, int v, int p) {
if (r < s or t < l) return;
if (l <= s and t <= r) return tr[p] *= v; PushDown(p); int mid = (s + t) >> 1;
Modify(l, r, s, mid, v, ls), Modify(l, r, mid + 1, t, v, rs); PushUp(p);
}
node Query(int l, int r, int s, int t, int p) {
if (r < s or t < l) return node();
if (l <= s and t <= r) return tr[p]; PushDown(p); int mid = (s + t) >> 1;
return Query(l, r, s, mid, ls) + Query(l, r, mid + 1, t, rs);
}
#undef ls
#undef rs
void Dfs1(int u, int f) {
dep[u] = dep[fa[u] = f] + 1, sz[u] = 1;
for (int v : e[u]) if (v != f) {
Dfs1(v, u), sz[u] += sz[v];
if (sz[v] > sz[son[u]]) son[u] = v;
}
}
void Dfs2(int u, int tp) {
top[u] = tp, dfn[u] = ++idx, ud[idx] = u;
if (!son[u]) return; Dfs2(son[u], tp);
for (int v : e[u]) if (v != fa[u] and v != son[u]) Dfs2(v, v);
}
void Modify(int x, int y, int v) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
Modify(dfn[top[x]], dfn[x], 1, n, v, 1);
x = fa[top[x]];
}
if (dep[x] > dep[y]) std::swap(x, y);
Modify(dfn[x], dfn[y], 1, n, v, 1);
}
node Query(int x, int y) {
node X, Y;
while (top[x] != top[y]) {
if (dep[top[x]] > dep[top[y]]) X += Query(dfn[top[x]], dfn[x], 1, n, 1).Swap(), x = fa[top[x]];
else Y = Query(dfn[top[y]], dfn[y], 1, n, 1) + Y, y = fa[top[y]];
}
if (dep[x] > dep[y]) return X + Query(dfn[y], dfn[x], 1, n, 1).Swap() + Y;
return X + Query(dfn[x], dfn[y], 1, n, 1) + Y;
}
int LCA(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
x = fa[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
void Add(int u, int v) { g[u].push_back(v), g[v].push_back(u); }
void Upd(int u) { ++Vit, vis[u] = false, g[u].clear(); }
void Build() {
lep(i, 1, k) id[i] = i;
std::sort(id + 1, id + 1 + k, [](const int&x , const int& y) { return dfn[h[x]] < dfn[h[y]]; });
stk[TOP = 1] = 1, Upd(1);
lep(j, 1, k) { int i = id[j];
if (h[i] != 1) {
int l = LCA(h[i], stk[TOP]);
if (l != stk[TOP]) {
while (dep[stk[TOP - 1]] > dep[l]) Add(stk[TOP - 1], stk[TOP]), --TOP;
if (stk[TOP - 1] == l) Add(l, stk[TOP--]);
else Upd(l), Add(l, stk[TOP]), stk[TOP] = l;
}
stk[++TOP] = h[i], Upd(h[i]), un[h[i]] = true;
} else un[1] = true;
}
lep(i, 1, TOP - 1) Add(stk[i], stk[i + 1]);
}
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
for (int v : g[u]) if (v != f and !vis[v]) {
GetRt(v, u, total), sz[u] += sz[v];
tmp[u] = std::max(tmp[u], sz[v]);
}
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
void Dfs1(int u, int f, int fro, node nw) {
nw += Query(f, u);
if (un[u]) val[fro] += nw.t, All += nw.t, ++cnt[fro], ++tot;
for (int v : g[u]) if (!vis[v] and v != f) Dfs1(v, u, fro, nw);
}
void Dfs2(int u, int f, int fro, node nw) {
nw += Query(f, u);
if (un[u]) ans[u] += All - val[fro] + (nw.t - 1) * (tot - cnt[fro]);
for (int v : g[u]) if (!vis[v] and v != f) Dfs2(v, u, fro, nw);
}
void Calc(int u) { All = tot = un[u];
for (int v : g[u]) if (!vis[v]) val[v] = cnt[v] = 0, Dfs1(v, u, v, node());
if (un[u]) ans[u] += All;
for (int v : g[u]) if (!vis[v]) Dfs2(v, u, v, node());
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total), Calc(rt), vis[rt] = true;
for (int v : g[rt]) if (!vis[v]) Solve(v, total - tmp[v]);
}
int main() {
scanf("%d%d", & n, & q);
lep(i, 1, n) scanf("%d", c + i); int u, v, y, op;
lep(i, 2, n) scanf("%d%d", & u, & v),
e[u].push_back(v), e[v].push_back(u);
Dfs1(1, 0), Dfs2(1, 1), Build(1, n, 1);
while (q--) {
scanf("%d", & op);
if (op == 1) scanf("%d%d%d", & u, & v, & y), Modify(u, v, y);
else {
scanf("%d", & k);
lep(i, 1, k) scanf("%d", h + i);
Build(), Solve(1, Vit);
lep(i, 1, k) printf("%lld ", ans[h[i]]), ans[h[i]] = un[h[i]] = 0;
Vit = 0; puts("");
}
}
return 0;
}
Tree MST
给定一棵带权(点权和边权)树,现有一张完全图,两点 \(x,y\) 之间的边长为 \(w_x+w_y+dis(x,y)\) 。
其中 \(dis(x,y)\) 表示树上两点之间的距离。
求完全图的最小生成树。
点击查看
求原图的 \(MST\) ,等价于将原图边集进行某种划分,对每个划分子集求 \(MST\) ,保留下这些边,再求 \(MST\) 。
看到路径距离考虑点分治。
每次只考虑跨过重心的两点之间的边,定义 \(dis_i\) 为 \(i\) 的到根路径,\(val_i=w_i+dis_i\) ,则两点之间的边权即为 \(val_i+val_j\) 。
将 \(val_i\) 最小的向其他点连边即可。
最后将保留的边跑一遍 \(Kruskal\) 。
保留下的边为 \(O(n\log n)\) 级别,总复杂度为 \(O(n\log^2 n)\) 。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, t) for (int i = H[u], t = e[i].v; i; i = e[i].n, t = e[i].v)
typedef long long ll;
const int _ = 2e5 + 7;
namespace G{
struct edge { int u, v; ll w; }; std::vector <edge> E;
int n, m, fa[_]; ll ans = 0;
void Add(int u, int v, ll w) { E.push_back({ u, v, w }); }
void Init(int _n) { n = _n; }
int Find(int x) { return fa[x] == x ? x : fa[x] = Find(fa[x]); }
void Merge(int x, int y, ll w) { if ((x = Find(x)) != (y = Find(y))) fa[x] = y, ans += w; }
ll Solve() {
lep(i, 1, n) fa[i] = i;
std::sort(E.begin(), E.end(), [](const edge& x, const edge& y){ return x.w < y.w; });
for (edge e : E) Merge(e.u, e.v, e.w);
return ans;
}
};
struct edge { int v, n, w; }e[_ << 1]; int H[_], cnte = 1;
int n, a[_], id[_]; ll val[_];
int sz[_], tmp[_], rt; bool vis[_];
void Add(int u, int v, int w) { e[++cnte] = edge { v, H[u], w }, H[u] = cnte; }
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
ep(i, u, v) if (!vis[v] and v != f)
GetRt(v, u, total), sz[u] += sz[v], tmp[u] = std::max(tmp[u], sz[v]);
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
void Dfs(int u, int f, ll w) {
id[++*id] = u, val[u] = a[u] + w;
ep(i, u, v) if (!vis[v] and v != f)
Dfs(v, u, w + e[i].w);
}
void Calc(int u) {
*id = 0; Dfs(u, 0, 0);
std::sort(id + 1, id + 1 + *id, [](const int& x, const int& y) { return val[x] < val[y]; });
lep(i, 2, *id) G::Add(id[1], id[i], val[id[1]] + val[id[i]]);
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total), Calc(rt), vis[rt] = true;
ep(i, rt, v) if (!vis[v]) Solve(v, total - tmp[v]);
}
int main() {
scanf("%d", & n); int u, v, w; G::Init(n);
lep(i, 1, n) scanf("%d", a + i);
lep(i, 2, n) scanf("%d%d%d", & u, & v, & w), Add(u, v, w), Add(v, u, w);
Solve(1, n);
printf("%lld\n", G::Solve());
return 0;
}
河童重工
给定两棵树,现有一张完全图,\(c(u, v) = dis_1(u, v) + dis_2(u, v)\) 。求 \(MST\) 。
点击查看
对 \(T1\) 点分治,定义每个点的权值为其深度,将当前处理的子树内点在 \(T2\) 的虚树建出来,我们获得了一个和上一题一样的子问题。
这里介绍一种新做法,对于每个点 \(x\) ,建立一个虚点 \(x'\) ,连接 \(c(x,x') = val_x\) 。
定义 \(fro_x\) 为离 \(x\) 最近的虚点, \(dis_x = dis(x, fro_x)\) 。
对于每一条边(包括和虚点相连的边) \((u, v)\), 从 \(fro_u\) 到 \(fro_v\) 连接一条 \(dis_u + dis_v +l(u, v)\) 的候选边。
其中 \(l(u, v)\) 是两点在 \(T2\) 上的距离。
然后将所有候选边做 \(Kruskal\) , 复杂度 \(O(n\log n\log (n\log n))\) 。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(G, i, u, t, h) for (int i = G.H[u], t = G.e[i].v, h = G.e[i].w; i; i = G.e[i].n, t = G.e[i].v, h = G.e[i].w)
const int _ = 2e5 + 7;
typedef long long ll;
const ll inf = 1e15;
int n;
namespace G{
struct edge { int u, v; ll w; }; std::vector <edge> E;
int fa[_];
void Init() { lep(i, 1, n) fa[i] = i; }
inline void Add(int u, int v, ll w) { if (u != v) E.push_back(edge{ u, v, w }); }
int Find(int x) { return fa[x] == x ? x : fa[x] = Find(fa[x]); }
ll Merge(int x, int y, ll w) { if ((x = Find(x)) != (y = Find(y))) { fa[x] = y, --n; return w; } return 0; }
ll Kruskal() {
std::sort(E.begin(), E.end(), [](const edge&x, const edge& y) { return x.w < y.w; });
ll ans = 0; for (edge k : E) ans += Merge(k.u, k.v, k.w);
return ans;
}
};
int dfn[_], fa[_], idx, st[_][21], lg[_], dep[_]; ll len[_];
int stk[_], top, h[_], k, fro[_]; ll val[_], dl[_];
int sz[_], tmp[_], rt; bool vis[_];
struct Tree{
struct edge{ int v, n; ll w; }e[_]; int H[_], cnte = 1;
void Add(int u, int v, ll w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void Read() { int u, v; ll w; lep(i, 2, n) scanf("%d%d%lld", & u, & v, & w), Add(u, v, w), Add(v, u, w); }
}T0, T1, T2;
void Init(int u, int f, ll d) {
dfn[u] = ++idx, st[idx][0] = u, dep[u] = dep[fa[u] = f] + 1, len[u] = d;
ep(T1, i, u, v, w) if (v != f) Init(v, u, d + w);
}
void Init() {
Init(1, 0, 0);
lep(i, 2, n) lg[i] = lg[i >> 1] + 1;
lep(j, 1, 20) lep(i, 1, n - (1 << j) + 1)
st[i][j] = dep[st[i][j - 1]] < dep[st[i + (1 << j - 1)][j - 1]] ? st[i][j - 1] : st[i + (1 << j - 1)][j - 1];
}
int LCA(int u, int v) {
if (dfn[u] > dfn[v]) std::swap(u, v);
int k = lg[dfn[v] - dfn[u] + 1],
p = (dep[st[dfn[u]][k]] < dep[st[dfn[v] - (1 << k) + 1][k]]
? st[dfn[u]][k] : st[dfn[v] - (1 << k) + 1][k]);
if (p == u) return u; else return fa[p];
}
inline void Upd(int u) { T2.H[u] = 0, fro[u] = u; }
inline void Add(int u, int v) { T2.Add(u, v, len[v] - len[u]); }
void Build() {
std::sort(h + 1, h + 1 + k, [](const int&x, const int&y) { return dfn[x] < dfn[y]; });
stk[top = 1] = 1, Upd(1), T2.cnte = 1; bool flag = false;
lep(i, 1, k) if (h[i] != 1) {
int l = LCA(stk[top], h[i]);
if (l != stk[top]) {
while (dep[stk[top - 1]] > dep[l]) Add(stk[top - 1], stk[top]), --top;
if (stk[top - 1] == l) Add(stk[top - 1], stk[top]), --top;
else Upd(l), val[l] = dl[l] = inf, Add(l, stk[top]), stk[top] = l;
}
stk[++top] = h[i], Upd(h[i]);
} else flag = true;
if (!flag) dl[1] = val[1] = inf;
lep(i, 1, top - 1) Add(stk[i], stk[i + 1]);
}
void Dfs1(int u, int f) {
ep(T2, i, u, v, w) if (v != f) {
Dfs1(v, u);
if (val[v] + w < val[u])
val[u] = val[v] + w, fro[u] = fro[v];
}
}
void Dfs2(int u, int f) {
G::Add(fro[u], u, val[u] + dl[u]);
ep(T2, i, u, v, w) if (v != f) {
if (val[u] + w < val[v])
val[v] = val[u] + w, fro[v] = fro[u];
Dfs2(v, u), G::Add(fro[u], fro[v], val[u] + val[v] + w);
}
}
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
ep(T0, i, u, v, w) if (!vis[v] and v != f)
GetRt(v, u, total), sz[u] += sz[v], tmp[u] = std::max(tmp[u], sz[v]);
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
void Dfs(int u, int f, ll d) {
h[++k] = u, val[u] = dl[u] = d;
ep(T0, i, u, v, w) if (!vis[v] and v != f) Dfs(v, u, d + w);
}
void Calc(int u) {
k = 0, Dfs(u, 0, 0); Build();
Dfs1(1, 0), Dfs2(1, 0);
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total), Calc(rt), vis[rt] = true;
ep(T0, i, rt, v, w) if (!vis[v]) Solve(v, total - tmp[v]);
}
int main() {
scanf("%d", & n);
T0.Read(), T1.Read(); Init(); G::Init();
Solve(1, n);
printf("%lld\n", G::Kruskal());
return 0;
}
模式字符串
给一棵字符树,问有多少条路径 \((u, v)\) 满足刚好是一个长度为 \(m\) 的字符串 \(T\) 重复若干次得来的。
点击查看
考虑拼接前缀和后缀,枚举子树与前面所有子树统计贡献,可以不重不漏。
具体地,处理 \(C/H[0][len]\) ,表示 子树/之前子树 长度为 \(len\) 的前缀/后缀串的个数。$( len \in \left[1, m\right]) $ 。
设 \(F[u][0/1]\) 表示节点 \(u\) 是否能对前缀 / 后缀造成贡献。
以前缀为例,如果当前节点的深度 \(> m\) ,则 \(F[u][0] = \left[F[fa[u][m]][0] \wedge Link(u, fa[u][m - 1]) = T\right]\) 。
其中, \(fa[u][m]\) 表示 \(u\) 的 \(m\) 级祖先, \(Link(u, v)\) 表示 \((u, v)\) 链上的字符所组成的串。
如果深度 \(\le m\) ,则 \(F[u][0] = \left[Link(u, rt) = T[1, dep_{rt} - dep_u + 1]\right]\) 。
其中, \(T[1, len]\) 表示 \(T\) 的长度为 \(len\) 的前缀。
后缀同理。
拼接时枚举前缀长度计数即可,注意重心处前后缀有重合。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 1e6 + 7;
typedef long long ll;
typedef unsigned long long ull;
int T, n, m; char s[_], t[_];
int sz[_], tmp[_], rt, cnt[_], top, TOP; bool vis[_], F[_][2];
std::vector <int> e[_]; ull Hsh[_], bse = 233, pre[_], suf[_], Pm, ans, C[2][_], H[2][_];
void Init() { Pm = 1;
lep(i, 1, m)
pre[i] = pre[i - 1] + t[i] * Pm,
suf[i] = suf[i - 1] + t[m - i + 1] * Pm,
Pm *= bse;
}
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
for (int v : e[u]) if (!vis[v] and v != f)
GetRt(v, u, total), sz[u] += sz[v], tmp[u] = std::max(tmp[u], sz[v]);
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
void Dfs(int u, int f) {
cnt[++top] = u, Hsh[u] = Hsh[f] * bse + s[u];
if (top > m) { TOP = (top - 1) % m + 1;
if (F[cnt[top - m]][0] && (Hsh[u] - Hsh[cnt[top - m]] * Pm == pre[m])) ++C[0][TOP], F[u][0] = true; else F[u][0] = false;
if (F[cnt[top - m]][1] && (Hsh[u] - Hsh[cnt[top - m]] * Pm == suf[m])) ++C[1][TOP], F[u][1] = true; else F[u][1] = false;
}
else {
if (Hsh[u] == pre[top]) ++C[0][top], F[u][0] = true; else F[u][0] = false;
if (Hsh[u] == suf[top]) ++C[1][top], F[u][1] = true; else F[u][1] = false;
}
for (int v : e[u]) if (!vis[v] and v != f) Dfs(v, u);
--top;
}
void Calc(int u, int total) {
cnt[top = 1] = u, Hsh[u] = s[u];
lep(i, 1, m) H[0][i] = H[1][i] = 0;
H[0][1] = F[u][0] = (s[u] == t[1]), H[1][1] = F[u][1] = (s[u] == t[m]);
for (int v : e[u]) if (!vis[v]) {
lep(i, 1, m) C[0][i] = C[1][i] = 0; Dfs(v, u);
lep(i, 1, m) ans += C[0][i] * H[1][m + 1 - i] + C[1][i] * H[0][m + 1 - i];
lep(i, 1, m) H[0][i] += C[0][i], H[1][i] += C[1][i];
}
}
void Solve(int u, int total) {
rt = 0, GetRt(u, 0, total), Calc(rt, total), vis[rt] = true;
for (int v : e[rt]) if (!vis[v]) Solve(v, total - tmp[v]);
}
int read() {
int x = 0; char c = getchar();
while (c < '0' or c > '9') c = getchar();
while (c>='0' and c<= '9') x = x * 10 + c - '0', c = getchar();
return x;
}
int main() {
T = read();
while (T--) {
n = read(), m = read();
lep(i, 1, n) while (!isalpha(s[i] = getchar()));
int u, v;
lep(i, 2, n) u = read(), v = read(),
e[u].push_back(v), e[v].push_back(u);
lep(i, 1, m) while (!isalpha(t[i] = getchar()));
Init(); Solve(1, n);
printf("%llu\n", ans); ans = 0;
lep(i, 1, n) e[i].clear(), vis[i] = false;
}
return 0;
}
边分治
概述
当有些时候,问题的难度与度数 / 子树个数有关时,点分治的复杂度难以控制,我们就采取边分治的办法。
与点分治类似,每次选取一条分治边,将树分成两部分,处理经过分治边的贡献,然后把这条边删去。 (通常搭配虚树食用)
单纯的边分治复杂度仍然是 \(O(n\log n)\) 。
实现细节
容易发现边分治会被菊花图卡成 \(O(n^2)\) ,所以我们需要对原树进行一些改造。
三(N)度化
以三度化为例,需要限制每个节点的度数最多只能为三,即改造原树为二叉树,且不能改变点对路径长度。
一种三度化的方法是
按照 \(DFS\) 顺序执行,对于当前节点 \(u\) ,遍历子节点 \(v\) 以及 \(w=c(u, v)\):
我们定义 \(lst\) 为目前可以挂儿子的节点(初始为 \(u\)) 。
- 将 \(lst\) 向 \(v\) 连一条 \(w\) 的边
- 如果当前 \(lst\) 已有 \(1\) 个儿子,则新建一个节点 \(tot\) ,从 \(lst\) 向 \(tot\) 连一条 \(0\) 的边,将 \(lst\) 修改为 \(tot\) 。
然后我们就重建了这棵树,并且不改变任意两点的路径长度。
(一般使用三度化或四度化,有些题目需要使用十度化等来优化常数)
//deg 是一个点最多有几个儿子
void Rebuild(int u, int f, ll d) {
int lst = u, son = 0; dep[u] = d;
for (auto k : G[u]) if (k.first != f) { int v = k.first; ll w = k.second;
if (son == deg - 1) Add(lst, ++tot, 0), Add(tot, v, w), lst = tot, son = 1;
else Add(lst, v, w), ++son;
Rebuild(v, u, d + w);
}
}
分治过程
边分治过程类似于点分治,只不过需要用链式前向星存图,并对边打上标记。
void GetHe(int u, int f, int total) {
sz[u] = 1; int tmp = 0;
ep(T1, i, u, v, w) if (!vis[i >> 1] and v != f) {
GetHe(v, u, total), sz[u] += sz[v], tmp = std::max(sz[v], total - sz[v]);
if (!he or tmp < mx) he = i, mx = tmp;
}
}
void Solve(int u, int total) {
he = 0, GetHe(u, 0, total); vis[he >> 1] = true;
if (!he) return;
int f = T1.e[he ^ 1].v, v = T1.e[he].v, t = sz[v];
Calc(f, v, T1.e[he].w); //这个小东西依旧是每份代码的难点
Solve(v, t), Solve(f, total - t);
}
例题
Freezing with Style
给定一颗带边权的树,求一条边数在 \([L,R]\) 之间的路径,并使得路径上边权的中位数最大。输出一条可行路径的两个端点。
点击查看
看到中位数,想到经典二分 trick ,将边权根据二分 \(mid\) 分为 \(1\) 和 \(-1\) 。
现在我们想要找到一条边数在 \([L, R]\) 之间的路径,使得边权和最大。
边分治,对于一侧,我们预处理出不同深度中到根权值和最大的点。
对于另一侧,我们 \(bfs\) ,这样深度一定不降, \([L-d, R-d]\) 的区间只会减少,单调队列即可。
注意,\(3\) 度化会使深度出现非不降的情况,如果暴力一点可以用堆,精细实现可以遇到长度为 \(0\) 的边就 \(Dfs\) 找到不为 \(0\) 的边转移,因为 \(0\) 的边是无用的。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, V, W, C) for (int i = H[u], V = e[i].v, W = e[i].w, C = e[i].c; i; i = e[i].n, V = e[i].v, W = e[i].w, C = e[i].c)
const int _ = 5e5 + 7;
const int inf = 1e9;
struct edge { int v, n, w, c; }e[_ << 2]; int H[_], cnte = 1;
struct node { int u, f, l, r;
friend bool operator >(const node&x, const node& y) { return x.l > y.l; };
};
int n, L, R, as, at, s, t, ans(-1), tot; int md, val[_] = {-inf};
int dep[_], a[_], sz[_], he, mx; bool vis[_];
std::vector <std::pair<int, int> > G[_];
void Add(int u, int v, int w, int c) { e[++cnte] = { v, H[u], w, c }, H[u] = cnte, e[++cnte] = { u, H[v], w, c }, H[v] = cnte; }
int deg = 10;
void Rebuild(int u, int f) {
int son = 0, lst = u;
for (auto k : G[u]) { int v = k.first, c = k.second; if (v == f) continue;
if (son == deg - 2) Add(lst, ++tot, 0, 0), lst = tot, Add(lst, v, 1, c), son = 1;
else Add(lst, v, 1, c), ++son;
Rebuild(v, u);
}
}
void GetHe(int u, int f, int total) {
sz[u] = 1; int tmp;
ep(i, u, v, w, c) if (!vis[i >> 1] and v != f) {
GetHe(v, u, total), sz[u] += sz[v]; tmp = std::max(sz[v], total - sz[v]);
if (!he or tmp < mx) he = i, mx = tmp;
}
}
int Upd(int x, int y) { return val[x] != val[y] ? (val[x] > val[y] ? x : y) : std::min(x, y); }
struct Queue{
int l, r, q[_];
void Init() { l = 1, r = 0; }
void Add(int x) { while (l <= r and Upd(x, q[r]) == x) --r; q[++r] = x; }
void Del(int x) { while (l <= r and dep[q[l]] > x) ++l; }
int Query() { return l <= r ? q[l] : 0; }
bool empty() { return l > r; }
}baka;
void Dfs(int u, int f, int d, int r, int mid) {
dep[u] = d, val[u] = r;
if (d > md) a[d] = u, md = d;
else a[d] = Upd(a[d], u);
ep(i, u, v, w, c) if (!vis[i >> 1] and v != f) {
if (w) Dfs(v, u, d + 1, r + ((c >= mid) * 2 - 1), mid);
else Dfs(v, u, d, r, mid);
}
}
bool Bfs(int u, int mid) { std::priority_queue <node, std::vector <node>, std::greater<node> > q;
int qL = md + 1; baka.Init(); q.push({u, 0, 0, 0});
while (!q.empty()) {
int u = q.top().u, f = q.top().f, l = q.top().l, r = q.top().r; q.pop();
while (qL and L - l <= qL - 1) baka.Add(a[--qL]);
baka.Del(R - l);
if (L - l <= qL and !baka.empty()) {
int x = baka.Query();
if (u <= n and val[x] + r >= 0) { s = x, t = u; return true; }
}
ep(i, u, v, w, c) if (!vis[i >> 1] and v != f) {
if (w) q.push(node{v, u, l + 1, r + ((c >= mid) * 2 - 1)});
else q.push(node{v, u, l, r, });
}
}
return false;
}
void Calc(int u, int v, int w, int c) {
int l = -1, r = 1e9, rs = 1, rt = n;
while (l < r and r > ans) { int mid = (l + r + 1) >> 1;
md = 0, a[0] = 0;
if (w) Dfs(u, 0, 1, (c >= mid) * 2 - 1, mid);
else Dfs(u, 0, 0, 0, mid);
if (Bfs(v, mid)) rs = s, rt = t, l = mid;
else r = mid - 1;
}
if (l > ans) ans = l, as = rs, at = rt;
}
void Solve(int u, int total) {
if (total == 1) return;
he = 0, GetHe(u, 0, total); vis[he >> 1] = true;
int f = e[he ^ 1].v, v = e[he].v, t = sz[v];
Calc(v, f, e[he].w, e[he].c);
Solve(v, t), Solve(f, total - t);
}
int main() {
scanf("%d%d%d", & n, & L, & R); int u, v, w; tot = n;
lep(i, 2, n) scanf("%d%d%d", & u, & v, & w),
G[u].push_back({v, w}), G[v].push_back({u, w});
Rebuild(1, 0); Solve(1, tot);
printf("%d %d\n", as, at);
return 0;
}
[WC2010] 重建计划
给定一颗带边权的树,求一条边数在 \([L,R]\) 之间的路径,并使得路径上边权的平均数最大。
点击查看
和上一个题同理,不过转化变成了分数规划。
二分平均值判断是否可以达到。
将每条边的权值减去 \(mid\) ,判断是否存在一条边数在 \([L, R]\) 之间的路径,使得权值和 \(\ge 0\) 。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, V, W, C) for (int i = H[u], V = e[i].v, W = e[i].w, C = e[i].c; i; i = e[i].n, V = e[i].v, W = e[i].w, C = e[i].c)
const int _ = 5e5 + 7;
const int inf = 1e9;
typedef double D;
const D eps = 1e-6;
struct edge { int v, n, w, c; }e[_ << 2]; int H[_], cnte = 1;
struct node { int u, f, l; D r;
friend bool operator >(const node&x, const node& y) { return x.l > y.l; };
};
int n, L, R, tot; int md; D val[_] = {-inf}, ans;
int dep[_], a[_], sz[_], he, mx; bool vis[_];
std::vector <std::pair<int, int> > G[_];
void Add(int u, int v, int w, int c) { e[++cnte] = { v, H[u], w, c }, H[u] = cnte, e[++cnte] = { u, H[v], w, c }, H[v] = cnte; }
int deg = 10;
void Rebuild(int u, int f) {
int son = 0, lst = u;
for (auto k : G[u]) { int v = k.first, c = k.second; if (v == f) continue;
if (son == deg - 2) Add(lst, ++tot, 0, 0), lst = tot, Add(lst, v, 1, c), son = 1;
else Add(lst, v, 1, c), ++son;
Rebuild(v, u);
}
}
void GetHe(int u, int f, int total) {
sz[u] = 1; int tmp;
ep(i, u, v, w, c) if (!vis[i >> 1] and v != f) {
GetHe(v, u, total), sz[u] += sz[v]; tmp = std::max(sz[v], total - sz[v]);
if (!he or tmp < mx) he = i, mx = tmp;
}
}
int Upd(int x, int y) { return val[x] != val[y] ? (val[x] > val[y] ? x : y) : std::min(x, y); }
struct Queue{
int l, r, q[_];
void Init() { l = 1, r = 0; }
void Add(int x) { while (l <= r and Upd(x, q[r]) == x) --r; q[++r] = x; }
void Del(int x) { while (l <= r and dep[q[l]] > x) ++l; }
int Query() { return l <= r ? q[l] : 0; }
bool empty() { return l > r; }
}baka;
void Dfs(int u, int f, int d, D r, D mid) {
dep[u] = d, val[u] = r;
if (d > md) a[d] = u, md = d;
else a[d] = Upd(a[d], u);
ep(i, u, v, w, c) if (!vis[i >> 1] and v != f) {
if (w) Dfs(v, u, d + 1, r + c - mid, mid);
else Dfs(v, u, d, r, mid);
}
}
bool Bfs(int u, D mid) { std::priority_queue <node, std::vector <node>, std::greater<node> > q;
int qL = md + 1; baka.Init(); q.push({u, 0, 0, 0});
while (!q.empty()) {
int u = q.top().u, f = q.top().f, l = q.top().l; D r = q.top().r; q.pop();
while (qL and L - l <= qL - 1) baka.Add(a[--qL]);
baka.Del(R - l);
if (L - l <= qL and !baka.empty()) {
int x = baka.Query();
if (val[x] + r >= 0) return true;
}
ep(i, u, v, w, c) if (!vis[i >> 1] and v != f) {
if (w) q.push(node{v, u, l + 1, r + c - mid});
else q.push(node{v, u, l, r});
}
}
return false;
}
void Calc(int u, int v, int w, int c) {
D l = 0, r = 1e6;
while (r - l > eps and r > ans) { D mid = (l + r) / 2;
md = 0, a[0] = 0;
if (w) Dfs(u, 0, 1, c - mid, mid);
else Dfs(u, 0, 0, 0, mid);
if (Bfs(v, mid)) l = mid;
else r = mid;
}
ans = std::max(ans, l);
}
void Solve(int u, int total) {
if (total == 1) return;
he = 0, GetHe(u, 0, total); vis[he >> 1] = true;
int f = e[he ^ 1].v, v = e[he].v, t = sz[v];
Calc(v, f, e[he].w, e[he].c);
Solve(v, t), Solve(f, total - t);
}
int main() {
scanf("%d%d%d", & n, & L, & R); int u, v, w; tot = n;
lep(i, 2, n) scanf("%d%d%d", & u, & v, & w),
G[u].push_back({v, w}), G[v].push_back({u, w});
Rebuild(1, 0); Solve(1, tot);
printf("%.3lf\n", ans);
return 0;
}
暴力写挂
给两棵树 \(T\) 和 \(T'\) , 找到一个点对 \((x, y)\) 最大化
\[depth(x)+depth(y)−(depth(LCA(x,y))+depth'(LCA'(x,y))) \]其中,\(depth(i)\) 表示 \(T\) 树中 点 \(1\) 到 \(i\) 的路径长度 , \(LCA(x, y)\) 表示 \(x\) 到 \(y\) 路径上距离 点 \(1\) 边数最少的点。
点击查看
拆式子:
使用边分治处理出现的路径问题。
考虑分治边将树划分成了两种颜色,\(dis(x, y)\) 可以拆成 \(dep_x + dep_y\) ,\(dep_x\) 表示 \(x\) 到分治边某一端点的距离。
记 \(val_x = dep_x + depth(x)\) ,对目前涉及到的点在 \(T'\) 中的虚树,我们有这样一个问题:
最大化黑白点对 \((x, y)\) 的贡献 \(val_x + val_y - 2\times depth'(LCA'(x, y))\)
经典的树形 \(DP\) ,在 \(LCA\) 处统计不同子树之间的配对即可。
最后记得考虑 \(x=y\) 的贡献,即 \(\max\{ depth(x) - depth'(x) \}\) 。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(G, i, u, t, w) for (int i = G.H[u], t = G.e[i].v, w = G.e[i].w; i; i = G.e[i].n, t = G.e[i].v, w = G.e[i].w)
const int _ = 1e6 + 7;
typedef long long ll;
const ll inf = 1e16;
int n;
struct Graph{
struct edge { int v, n; ll w; }e[_]; int H[_], cnte = 1;
void Add(int u, int v, ll w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void Read() { int u, v; ll w; lep(i, 2, n) scanf("%d%d%lld", & u, & v, & w), Add(u, v, w), Add(v, u, w); }
}T0, T1, T2;
int tot, dfn[_], st[_][21], idx, lg[_], len[_], fa[_];
int h[_], k, stk[_], top, col[_]; ll ans(-inf), val[_], dp[_][2], dep[_], _dep[_];
int sz[_], he, mx; bool vis[_];
std::vector <std::pair<int, ll> > G[_];
int deg = 3;
void Add(int u, int v, ll w) { T1.Add(u, v, w), T1.Add(v, u, w); }
void Rebuild(int u, int f, ll d) {
int lst = u, son = 0; dep[u] = d;
for (auto k : G[u]) if (k.first != f) { int v = k.first; ll w = k.second;
if (son == deg - 1) Add(lst, ++tot, 0), Add(tot, v, w), lst = tot, son = 1;
else Add(lst, v, w), ++son;
Rebuild(v, u, d + w);
}
}
void Init(int u, int f, ll d) {
dfn[u] = ++idx, st[idx][0] = u, _dep[u] = d, len[u] = len[fa[u] = f] + 1;
ans = std::max(ans, 1ll * dep[u] - _dep[u]);
ep(T2, i, u, v, w) if (v != f) Init(v, u, d + w);
}
void Init() {
lep(i, 2, n) lg[i] = lg[i >> 1] + 1;
Rebuild(1, 0, 0); Init(1, 0, 0);
lep(j, 1, 20) lep(i, 1, n - (1 << j) + 1)
st[i][j] = len[st[i][j - 1]] < len[st[i + (1 << j - 1)][j - 1]] ? st[i][j - 1] : st[i + (1 << j - 1)][j - 1];
}
int LCA(int u, int v) {
if (dfn[u] > dfn[v]) std::swap(u, v);
int k = lg[dfn[v] - dfn[u] + 1], p = len[st[dfn[u]][k]] < len[st[dfn[v] - (1 << k) + 1][k]] ?
st[dfn[u]][k] : st[dfn[v] - (1 << k) + 1][k];
return p == u ? u : fa[p];
}
inline void Upd(int u) { T0.H[u] = 0; }
inline void Add(int u, int v) { T0.Add(u, v, _dep[v] - _dep[u]); }
void Build() {
std::sort(h + 1, h + 1 + k, [](const int&x, const int& y) { return dfn[x] < dfn[y]; });
T0.cnte = 1, stk[top = 1] = 1, Upd(1); bool flag = false;
lep(i, 1, k) if (h[i] != 1) {
if (h[i] > n) continue;
int l = LCA(h[i], stk[top]);
if (l != stk[top]) {
while (len[stk[top - 1]] > len[l]) Add(stk[top - 1], stk[top]), --top;
if (stk[top - 1] == l) Add(l, stk[top--]);
else Upd(l), col[l] = -1, Add(l, stk[top]), stk[top] = l;
}
stk[++top] = h[i], Upd(h[i]);
} else flag = true;
if (!flag) col[1] = -1;
lep(i, 1, top - 1) Add(stk[i], stk[i + 1]);
}
void GetHe(int u, int f, int total) {
sz[u] = 1; int tmp = 0;
ep(T1, i, u, v, w) if (!vis[i >> 1] and v != f) {
GetHe(v, u, total), sz[u] += sz[v], tmp = std::max(sz[v], total - sz[v]);
if (!he or tmp < mx) he = i, mx = tmp;
}
}
void Dfs(int u, int f, ll d, int c) {
h[++k] = u, val[u] = d + dep[u], col[u] = c;
ep(T1, i, u, v, w) if (!vis[i >> 1] and v != f) Dfs(v, u, d + w, c);
}
void Dfs(int u, int f) {
dp[u][0] = dp[u][1] = -inf;
if (~col[u]) dp[u][col[u]] = val[u];
ep(T0, i, u, v, w) if (v != f) {
Dfs(v, u);
ans = std::max(ans, std::max(dp[u][0] + dp[v][1], dp[v][0] + dp[u][1]) / 2 - _dep[u]);
dp[u][0] = std::max(dp[u][0], dp[v][0]), dp[u][1] = std::max(dp[u][1], dp[v][1]);
}
}
void Calc(int u, int v, ll w) { k = 0, Dfs(u, 0, w, 0), Dfs(v, 0, 0, 1), Build(); Dfs(1, 0); }
void Solve(int u, int total) {
he = 0, GetHe(u, 0, total); vis[he >> 1] = true;
if (!he) return;
int f = T1.e[he ^ 1].v, v = T1.e[he].v, t = sz[v];
Calc(f, v, T1.e[he].w);
Solve(v, t), Solve(f, total - t);
}
int main() {
scanf("%d", & n), tot = n; int u, v; ll w;
lep(i, 2, n) scanf("%d%d%lld", & u, & v, & w),
G[u].push_back({v, w}), G[v].push_back({u, w});
T2.Read(); Init(); Solve(1, tot);
printf("%lld\n", ans);
return 0;
}
通道
给定三棵树,最大化 \(dis1(u, v) + dis2(u, v) + dis3(u, v)\) 。
点击查看
第一棵树同样边分治,然后在第二棵树上建带颜色虚树。
现在考虑第三棵树怎么做。
目前我们的式子是
在虚树上固定 \(LCA\) ,记 \(val(u) = d_1(u) + d_2(u)\) ,忽略常数后,我们需要最大化 \(u\) 的不同子树中的点对 \((u,v)\) 如下式子:
发现是树上点集直径,我们有结论:
在边权都是正数的情况下,树上两个点集的并的直径的端点一定是原本两个点集各自直径的端点之二。
然后我们就可以合并状态了,记 \(dp[u][0/1]\) 为 \(u\) 子树中颜色为 白/黑 的点集的直径端点,合并时枚举每一种端点情况即可。
求答案时注意颜色要不同。
直接实现是 \(O(n\log^2 n)\) 的,但是可以通过建虚树时使用 \(O(n\log n) \sim O(1)\) \(LCA\) 以及使用归并对 \(dfn\) 进行排序做到 \(O(n\log n)\) 。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(G, i, u, t, w) for (ll i = G.H[u], t = G.e[i].v, w = G.e[i].w; i; i = G.e[i].n, t = G.e[i].v, w = G.e[i].w)
const int _ = 1e6 + 7;
typedef long long ll;
const ll inf = 1e16;
int n;
struct Graph{
struct edge { int v, n; ll w; }e[_]; int H[_], cnte = 1;
void Add(int u, int v, ll w) { e[++cnte] = { v, H[u], w }, H[u] = cnte; }
void Read() { int u, v; ll w; lep(i, 2, n) scanf("%d%d%lld", & u, & v, & w), Add(u, v, w), Add(v, u, w); }
}T0, T1, T2, T3;
int lg[_];
struct ST{
int dfn[_], st[_][21], idx, len[_], fa[_]; ll dep[_];
void Init(Graph& A, int u, int f, ll d) {
dfn[u] = ++idx, st[idx][0] = u, dep[u] = d, len[u] = len[fa[u] = f] + 1;
ep(A, i, u, v, w) if (v != f) Init(A, v, u, d + w);
}
void Init(Graph& A) {
Init(A, 1, 0, 0);
lep(j, 1, 20) lep(i, 1, n - (1 << j) + 1)
st[i][j] = len[st[i][j - 1]] < len[st[i + (1 << j - 1)][j - 1]] ? st[i][j - 1] : st[i + (1 << j - 1)][j - 1];
}
int LCA(int u, int v) {
if (dfn[u] > dfn[v]) std::swap(u, v);
int k = lg[dfn[v] - dfn[u] + 1], p = len[st[dfn[u]][k]] < len[st[dfn[v] - (1 << k) + 1][k]] ?
st[dfn[u]][k] : st[dfn[v] - (1 << k) + 1][k];
return p == u ? u : fa[p];
}
ll Len(int u, int v) { return dep[u] + dep[v] - 2 * dep[LCA(u, v)]; }
}S2, S3;
ll val[_], ans(-inf);
ll Val(int a, int b) { return val[a] + val[b] + S3.Len(a, b); }
struct node {
int a, b;
node(int _a = 0, int _b = 0) { a = _a, b = _b; }
void Upd(int s, int t) { if (Val(s, t) > Val(a, b)) a = s, b = t; }
friend node operator + (const node &x, const node &y) {
node z; int u = x.a, v = x.b, a = y.a, b = y.b;
z.a = u, z.b = a; z.Upd(u, b), z.Upd(v, a), z.Upd(v, b), z.Upd(a, b), z.Upd(u, v);
return z;
}
}dp[_][2];
int tot;
int h[_], h1[_], stk[_], top, col[_];
int sz[_], he, mx; bool vis[_];
std::vector <std::pair<int, ll> > G[_];
int deg = 10;
void Add(int u, int v, ll w) { T1.Add(u, v, w), T1.Add(v, u, w); }
void Rebuild(int u, int f) {
int lst = u, son = 0;
for (auto k : G[u]) if (k.first != f) { int v = k.first; ll w = k.second;
if (son == deg - 1) Add(lst, ++tot, 0), Add(tot, v, w), lst = tot, son = 1;
else Add(lst, v, w), ++son;
Rebuild(v, u);
}
}
void Init() {
lep(i, 2, n) lg[i] = lg[i >> 1] + 1;
Rebuild(1, 0); S2.Init(T2), S3.Init(T3);
}
inline void Upd(int u) { T0.H[u] = 0; }
inline void Add(int u, int v) { T0.Add(u, v, 0); }
void Build(int l, int r) {
T0.cnte = 1, stk[top = 1] = 1, Upd(1); bool flag = false;
lep(i, l, r) if (h[i] != 1) {
if (h[i] > n) continue;
int l = S2.LCA(h[i], stk[top]);
if (l != stk[top]) {
while (S2.len[stk[top - 1]] > S2.len[l]) Add(stk[top - 1], stk[top]), --top;
if (stk[top - 1] == l) Add(l, stk[top--]);
else Upd(l), col[l] = -1, Add(l, stk[top]), stk[top] = l;
}
stk[++top] = h[i], Upd(h[i]);
} else flag = true;
if (!flag) col[1] = -1;
lep(i, 1, top - 1) Add(stk[i], stk[i + 1]);
}
void GetHe(int u, int f, int total) {
sz[u] = 1; int tmp = 0;
ep(T1, i, u, v, w) if (!vis[i >> 1] and v != f) {
GetHe(v, u, total), sz[u] += sz[v], tmp = std::max(sz[v], total - sz[v]);
if (!he or tmp < mx) he = i, mx = tmp;
}
}
void Dfs(int u, int f, ll d, int c) {
val[u] = d + S2.dep[u], col[u] = c;
ep(T1, i, u, v, w) if (!vis[i >> 1] and v != f) Dfs(v, u, d + w, c);
}
void Dfs(int u, int f) {
dp[u][0] = dp[u][1] = node();
if (~col[u]) dp[u][col[u]] = node(u, 0); ll res = 0; int a, b, s, t, x, y, p, q;
ep(T0, i, u, v, w) if (v != f) {
Dfs(v, u);
a = dp[u][0].a, b = dp[u][0].b, s = dp[u][1].a, t = dp[u][1].b,
x = dp[v][0].a, y = dp[v][0].b, p = dp[v][1].a, q = dp[v][1].b; res = 0;
res = std::max(res, std::max(std::max(Val(a, p), Val(a, q)), std::max(Val(b, p), Val(b, q))));
res = std::max(res, std::max(std::max(Val(s, x), Val(s, y)), std::max(Val(t, x), Val(t, y))));
ans = std::max(ans, res - 2 * S2.dep[u]);
dp[u][0] = dp[u][0] + dp[v][0], dp[u][1] = dp[u][1] + dp[v][1];
}
}
void Solve(int u, int total, int l) {
if (total == 1) { h[l] = u; return; }
he = 0, GetHe(u, 0, total); vis[he >> 1] = true;
int f = T1.e[he ^ 1].v, v = T1.e[he].v, t = sz[v], HE = he; ll w = T1.e[he].w;
Solve(v, t, l), Solve(f, total - t, l + t);
int i = l, j = l + t, k = l;
while (i <= l + t - 1 and j <= l + total - 1) {
if (S2.dfn[h[i]] < S2.dfn[h[j]]) h1[k++] = h[i++];
else h1[k++] = h[j++];
}
while (i <= l + t - 1) h1[k++] = h[i++];
while (j <= l + total - 1) h1[k++] = h[j++];
lep(i, l, k - 1) h[i] = h1[i];
Dfs(f, 0, w, 0), Dfs(v, 0, 0, 1);
Build(l, l + total - 1), Dfs(1, 0);
vis[HE >> 1] = false;
}
int main() { val[0] = -inf;
scanf("%d", & n), tot = n; int u, v; ll w;
lep(i, 2, n) scanf("%d%d%lld", & u, & v, & w),
G[u].push_back({v, w}), G[v].push_back({u, w});
T2.Read(), T3.Read(); Init(); Solve(1, tot, 1);
printf("%lld\n", ans);
return 0;
}
点分树
概述
当我们需要处理多次的路径询问时,每次做一遍点分治的复杂度无法接受,但每次点分治的过程都是类似的,我们可以离线下来。
具体的,将每层的分治中心向下一层分治中心连边,建成一棵新的树,我们叫它点分树。
点分树有如下性质:
- 树高只有 \(O(\log n)\)
很显然,因为点分治只会进行 \(\log n\) 层。
- 点对 \((u, v)\) 在点分树上的 \(LCA\) ,一定在原树 \((u, v)\) 的路径上。
点分树的 \(LCA\) 意味着,将这个点从原树中删去,则 \((u, v)\) 不连通。
- 每个节点代表着一个连通块,且某个点的所有祖先即它需要参与考虑的所有连通块。
参考点分治过程。
实现细节
void Add(int u, int v) { g[u].push_back(v), pr[v] = u; }
int Build(int u, int total) {
rt = 0, GetRt(u, 0, total); int RT = rt; vis[rt] = true;
C[rt][0].resize(total + 2), C[rt][1].resize(total + 2);
for (int v : e[RT]) if (!vis[v]) Add(RT, Build(v, total - tmp[v]));
return RT;
}
例题
【模板】点分树 | 震波
在线处理一棵带权树,支持两种操作
0 u k: 输出 \(\sum_{dis(u, v)\le k}val_v\)
1 u k: 修改 \(val_u = k\)
点击查看
\(ST\) \(O(1)\) 处理距离。
考虑点分树上每次询问的形式,对于询问点 \(u\) ,对于其到根路径上的每个点 \(p\),考虑和 \(u\) 不在 \(p\) 同一棵子树内的节点 \(v\) ,只要 \(dis(u, p) + dis(v, p) \le k\) , \(v\) 就会产生贡献,即 \(dis(v, p) \le k - dis(u, p)\) 。
发现其满足前缀的形式,使用树状数组即可。
具体的,扣子树贡献操作可以通过维护两个 \(BIT\) ,一个下标为到当前点距离,一个下标为到父亲距离来实现。
树状数组空间要开子树大小 \(+2\) ,保证不会 \(RE\) 或 \(MLE\) 。
实现可以看代码。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 1e5 + 7;
typedef long long ll;
int n, m, val[_], dfn[_], dep[_], fa[_], st[_][21], idx, lg[_];
int ans, sz[_], tmp[_], rt, pr[_]; bool vis[_];
std::vector <int> e[_], g[_];
std::vector <int> C[_][2];
void Init(int u, int f) {
dfn[u] = ++idx, st[idx][0] = u, dep[u] = dep[fa[u] = f] + 1;
for (int v : e[u]) if (v != f) Init(v, u);
}
void Add(int u, int v) { g[u].push_back(v), pr[v] = u; }
void GetRt(int u, int f, int total) {
sz[u] = 1, tmp[u] = 0;
for (int v : e[u]) if (!vis[v] and v != f)
GetRt(v, u, total), sz[u] += sz[v], tmp[u] = std::max(tmp[u], sz[v]);
tmp[u] = std::max(tmp[u], total - sz[u]);
if (!rt or tmp[u] < tmp[rt]) rt = u;
}
int Build(int u, int total) {
rt = 0, GetRt(u, 0, total); int RT = rt; vis[rt] = true;
C[rt][0].resize(total + 2), C[rt][1].resize(total + 2);
for (int v : e[RT]) if (!vis[v]) Add(RT, Build(v, total - tmp[v]));
return RT;
}
int MIN(int u, int v) { return dep[u] < dep[v] ? u : v; }
int LCA(int u, int v) {
if (dfn[u] > dfn[v]) std::swap(u, v);
int k = lg[dfn[v] - dfn[u] + 1], p = MIN(st[dfn[u]][k], st[dfn[v] - (1 << k) + 1][k]);
return p == u ? u : fa[p];
}
int Dis(int u, int v) { return dep[u] + dep[v] - 2 * dep[LCA(u, v)]; }
void Add(int u, int opt, int x, int k) { ++x; while (x < C[u][opt].size()) C[u][opt][x] += k, x += x & -x; }
int Query(int u, int opt, int x) { if (x < 0) return 0; x = std::min((int)C[u][opt].size() - 1, x + 1); int res = 0; while (x) res += C[u][opt][x], x -= x & -x; return res; }
void Modify(int u, int k) { int x = u;
while (x) {
Add(x, 0, Dis(x, u), k);
if (pr[x]) Add(x, 1, Dis(pr[x], u), k);
x = pr[x];
}
}
int Query(int u, int k) { int res = Query(u, 0, k), x = u;
while (pr[x]) {
res += Query(pr[x], 0, k - Dis(pr[x], u)) - Query(x, 1, k - Dis(pr[x], u));
x = pr[x];
}
return res;
}
void Init() {
lep(i, 2, n) lg[i] = lg[i >> 1] + 1;
Init(1, 0);
lep(j, 1, 20) lep(i, 1, n - (1 << j) + 1)
st[i][j] = MIN(st[i][j - 1] , st[i + (1 << j - 1)][j - 1]);
Build(1, n); lep(i, 1, n) Modify(i, val[i]);
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, n) scanf("%d", val + i); int u, v;
lep(i, 2, n) scanf("%d%d", & u, & v),
e[u].push_back(v), e[v].push_back(u);
Init(); int op, k;
while (m--) {
scanf("%d%d%d", & op, & u, & k);
u ^= ans, k ^= ans;
if (op) Modify(u, k - val[u]), val[u] = k;
else printf("%d\n", ans = Query(u, k));
}
return 0;
}
时间仓促,如有错误欢迎指出,欢迎在评论区讨论,如对您有帮助还请点个推荐、关注支持一下

 点分治 + 边分治 + 点分树
点分治 + 边分治 + 点分树

 浙公网安备 33010602011771号
浙公网安备 33010602011771号