字符串 - 后缀自动机(SAM)

简述

维护字符串所有子串的数据结构，也是一个 \(DAG\)。
本文内容仅包括你该如何做，并不含算法的正确性分析和正确的理解。
更多内容请静待作者更新。
不过本文仍值得一阅。

前置需知

对于一个子串 \(T\)，它在原串 \(S\) 中的出现位置组成了一个集合，记作 \(Endpos(T)\) 。

比如 \(S=[ababc]\)，\(Endpos([ab]) = \left\{ 2, 4 \right\}\), \(Endpos([aba]) = \left\{ 3\right\}\)。

我们称 \(Endpos\) 完全相同的子串组成的集合叫做一个等价类，称其中长度最长的等价类为其代表元素。
例如上面的例子，其中 \([ab]\), \([b]\) 就组成了一个等价类。

我们可以发现等价类的一些性质。

\(\mathrm{属于同一个等价类的子串，一定存在后缀关系，并且长度连续}\)

这是很显然的性质，因为他们的结尾位置都完全相同。
对于最长的代表元素，等价类中的其他子串一定是它的后缀。

\(\mathrm{等价类之间也可能存在后缀关系}\)

如图：

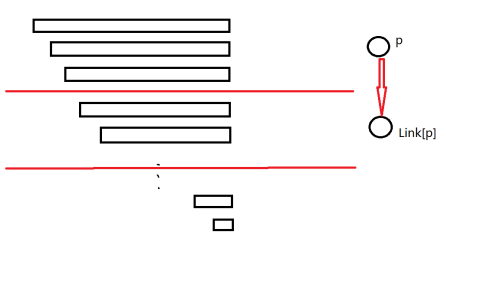
红线分隔开不同等价类，一个等价类对于一个状态。
红色箭头表示后缀指针，之后统一称作 \(Link\)。

如果一个等价类中元素全是另一个等价类 \(p\) 中元素的后缀，那么我们就将 \(p\) 的后缀指针 \(Link\) 指向这个等价类。
可以发现，\(Endpos(p)\subset Endpos(Link[p])\)。

特别的，我们将最短子串长度为 \(1\) 的等价类 \(Link\) 指向空串。

\(\mathrm{不重不漏！}\)

同样的根据定义，所有的等价类中子串的并一定是原串的子串集。
并且不同的等价类的交一定为 \(\varnothing\)。

也就是说，我们存储的等价类刚好 \(\mathrm{不重不漏}\) 地遍历了原串的所有子串。
这是后缀自动机状态存储重要的性质。

建立

这也是 \(SAM\) 最关键的操作了，我们采取在线增广的方式解决。
我们称一个状态 \(p\) 通过字符 \(c\) 的转移边能转移到状态 \(q\)，
当且仅当 \(p\) 中的所有子串拼接上字符 \(c\) 后全部属于 \(q\)。
记一个状态中代表元素的长度为 \(Len[i]\)。

假设我们已经求出了 \(S[1,i-1]\) 的后缀自动机，我们尝试插入 \(c=S[i]\)，来看看会对 \(SAM\) 造成什么修改。

看图：

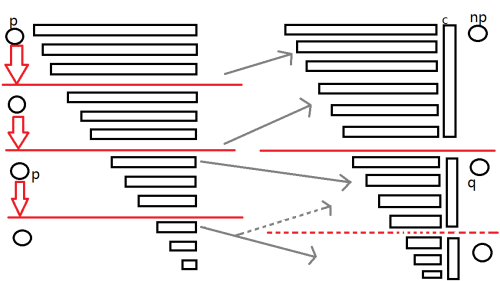
上一个插入的状态为 \(p\)，当前插入状态 \(np\)。
根据定义，我们可以令 \(len[np]=len[p]+1,ch[p][c]=np\)，即从 \(S[1,i-1]\) 添加 \(c\) 到 \(S[1,i]\)。

接下来，我们需要对 \(SAM\) 的其他结构进行修改。
让 \(p\) 跳后缀链接迭代其他节点 \(p^{\prime}\)，如果 \(p^{\prime}\) 没有一条 \(c\) 的转移边，就像图中第二层的状态，就连一条 \(c\) 的转移边到 \(p\)，因为没有其他的地方以这个状态结尾。

如果一直没有 \(p^{\prime}\) 有 \(c\) 的转移边，则将 \(Link[np]\) 连向空状态。
如果有，对于这个 \(p^{\prime}\) (以下记作 \(p\) )，记 \(q=ch[p][c]\) 。

看图，如果 \(q\) 状态没有最上面那部分子串，那么它刚好可以做 \(np\) 的后缀链接指向的状态。
即 \(Len[q] = Len[p] + 1\) 时， \(Link[np] = q\) 。

但是很多时候，并没有那么简单，根据定义要求新建一个状态 \(nq\) 表示 \(p\) 接上一个 \(c\) 转移到的状态。
同时， \(Len[nq] = len[p] + 1\) 。

如图：

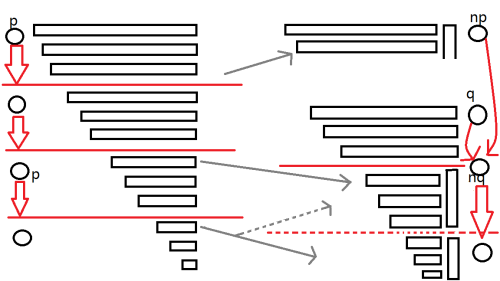
同样的根据定义，因为 \(nq\) 为原来 \(q\) 的子集，所以转移边需要继承。
并且 \(q\) 的后缀链接指向 \(nq\) ，\(nq\) 的后缀链接继承原来 \(q\) 的后缀链接。
因为 \(nq\) 继承了 \(q\) 的大部分信息，在有些博客中这个节点被称作 \(clone\) （克隆）。

同时，其他状态的转移边也会发生一定改变（即实际情况为虚线所示），原本指向 \(q\) 的状态现在要指向 \(nq\)。
容易发现这样的状态一定可以通过 \(p\) 跳后缀链接迭代到达（包括 \(p\) 本身）。
为什么全部都要修改呢？因为 \(p\) 已经可以通过转移边指向 \(nq\) 了，接下来遍历到的状态一定是 \(p\) 的后缀，
也就只能转移到 \(nq\) 而不是 \(q\) 了。

现在，\(np\) 的 \(Link\) 便可以指向 \(nq\) 了，可以把图左右对照来看。

至此，我们已经解决了插入字符的操作。

代码示例：


void Extend(int c) {
    int p = Last, np = ++idx; Last = np;//Last , idx 初始值均为 1，即把 1 号状态作为空状态
    len[np] = len[p] + 1;
    while (p and !ch[p].count(c)) ch[p][c] = np, p = Link[p];
    if (!p) Link[np] = 1;
    else {
        int q = ch[p][c];
        if (len[q] == len[p] + 1) Link[np] = q;
        else {
            int nq = ++idx;
            ch[nq] = ch[q], Link[nq] = Link[q];
            len[nq] = len[p] + 1, Link[np] = Link[q] = nq;
            while (p and ch[p][c] == q) ch[p][c] = nq, p = Link[p];
        }
    }
    ++num[np];
}

补充

\(upd\) \(on\) 2025-07-20 19:55:08 星期日

今天重学了一遍 \(SAM\) ，来补充一下上述做法的原理。

每插入一个字符，先考虑对原本等价类种类的影响。
记原本的串为 \(s\) ，现插入一个字符 \(c\) ，而原本 \(s\) 的子串中会被影响的，一定是 \(s + c\) 的后缀。
记之前存在的 \(s + c\) 的最长后缀为 \(t\) ，如果 \(t\) 就是所在等价类中最长的一个，那么他们的 \(Endpos\) 整体都 \(\cup (|s| + 1)\) 。
比如 bacaba|c ， \(t = [bac]\) ，可以直接 \(\cup\) 。

否则，那么 \(t\) 和等价类中比 \(t\) 长的串就拥有了不同的 \(Endpos\) ，也就是 \(|s| + 1\) ，就要从原本的等价类中分裂出来，成为一个新的等价类。
比如 cbacaba|c ， \(t = [bac]\) ，和 \([cbac]\) 不属于同一个等价类了，分裂。

而那些 \(t\) 的后缀，一定可以全部 \(\cup (|s| + 1)\) ，所以，直接保留原本的结构即可。

做法没看懂的读完这段话后回去对照一下，上述代码就是对这段话的模拟。

维护信息

子串出现次数

发现上面代码中的 \(num\) 数组了吗，它就是用来维护子串出现次数的，其实也就是 \(Endpos\) 的大小。
同样的根据定义，一个状态（即等价类）中的子串出现次数是一样的。
因为 \(Link\) 链接具有严格的后缀关系，所以它构成了一棵树，并且叶子状态就代表前缀。
（~~所以后缀自动机的 Link 树其实是前缀树~~）

对于一个等价类，如图：

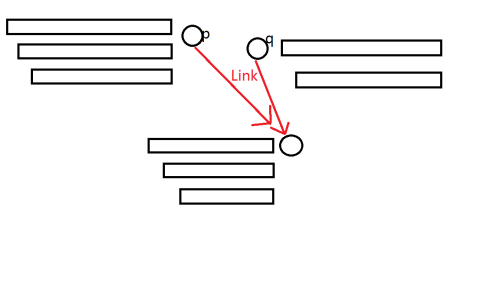
对于属于 \(Endpos(p)\) 的位置， \(Link[p]\) 也一定出现了，\(q\) 对 \(Link[q]\) 的贡献同理。
同时，因为 \(p\) 和 \(q\) 中的字符串本质不同，所以他们出现的位置也肯定不同，对 \(Link[p]\) 的贡献 \(\mathrm{不重不漏}\)。
不重是显然的，为什么不漏呢？
考虑对于每个状态的代表元素，\(Link\) 指向它的状态的最短子串，就是在这个代表元素前面接上不同的字符组成的，所以不漏。
不过这个结论有时是有问题的，就是对于每个前缀及与前缀在同一个等价类中的子串，它没有办法通过 \(Link\) 在前面接上一个字符。
每次插入的前缀状态出现次数初始化为 \(1\)，然后对 \(Link\) 树求子树和即可。

另外的，因为 \(Link[p]\) 边连接的状态长度具有严格的偏序关系，所以对长度进行计数排序后累加，就可以写成常数更小的非递归写法。


void Gets() {
    lep(i, 1, idx) tot[len[i]]++; //idx 为 SAM 状态数
    lep(i, 1, n) tot[i] += tot[i - 1];
    lep(i, 1, idx) sa[tot[len[i]]--] = i;
    rep(i, idx, 1) num[Link[sa[i]]] += num[sa[i]];
    lep(i, 1, idx) if (num[i] > 1) ans = std::max(ans, num[i] * len[i]);
}
//Luogu P3804 答案统计部分

第 \(k\) 小子串

从空状态走转移边，就是一个在末尾添加字符的过程，不同的路径对应着不同的子串，并且同样是 \(\mathrm{不重不漏}\)。
所以求第 \(k\) 小子串即求第 \(k\) 小路径，所以类比平衡树求第 \(k\) 小。
具体的，先预处理出每条转移边能到达的状态数，然后 \(Dfs\) 即可。


void Init() {
    lep(i, 1, idx) ++tot[len[i]], sum[i] = (i != 1);
    lep(i, 1, n) tot[i] += tot[i - 1];
    lep(i, 1, idx) sa[tot[len[i]]--] = i;
    
    rep(i, idx, 1) for (auto t : ch[sa[i]])
        sum[sa[i]] += sum[t.second];
}
void Dfs(int u, int k) {
    if (k <= (u != 1)) return;
    k -= (u != 1);
    for (auto t : ch[u]) { int v = t.second;
        if (k > sum[v]) k -= sum[v];
        else { putchar(t.first + 'a'); Dfs(v, k); return; }
    }
}
//SP7258

本质不同的子串个数

所有状态中子串个数，因为等价类中长度连续，所以答案即为 \(\sum_i len[i]-len[Link[i]]\) 。


void Extend(int c) {
    int p = Last, np = ++idx; Last = np;
    len[np] = len[p] + 1;
    while (p and !ch[p].count(c)) ch[p][c] = np, p = Link[p];
    
    if (!p) Link[np] = 1;
    else {
        int q = ch[p][c];
        if (len[q] == len[p] + 1) Link[np] = q;
        else {
            int nq = ++idx;
            ch[nq] = ch[q], Link[nq] = Link[q], len[nq] = len[p] + 1;
            Link[np] = Link[q] = nq;
            while (p and ch[p][c] == q) ch[p][c] = nq, p = Link[p];
        }
    }
    ans += len[np] - len[Link[np]];
}//SP705

可以发现这是一个动态过程。

最小表示法

将原串 \(S\) 复制一份接到后面，求最小的长度为 \(|S|\) 的子串。


void Solve(int u, int len) {
    if (len == n) return;
    printf("%d ", ch[u].begin()->first);
    Solve(ch[u].begin()->second, len + 1);
}//Luogu P1368

两个串的最长公共子串

对于其中一个串 \(S\) 建立后缀自动机，对于另一个串 \(T\) ，我们试图对其的每一个前缀找到可以匹配的最大后缀长度 \(l\) 。
答案即为 \(\max\left\{ l\right\}\) 。

考虑类似于 \(AC\) 自动机的匹配过程，记录当前所处状态 \(v\) 和 \(l\) 。
我们处理到当前字符 \(c\) ，如果 \(v\) 存在 \(c\) 的转移边，则转移，并且 \(l++\) 。
如果不存在，我们尝试缩短 \(l\) 以匹配上 \(c\)，让 \(v\) 通过后缀链接访问其后缀状态，尝试匹配。


int Gets(int c) {
    while (v != 1 and !ch[v].count(c)) v = Link[v], l = len[v];
    if (ch[v].count(c)) v = ch[v][c], ++l;
}
void Solve() {
    lep(i, 1, m) {
        Gets(t[i] - 'a');
        ans = std::max(ans, l);
    }
}//SP1811

Loading

幽光闪烁