算法笔记 - 联通性相关
相关概念
- 图 : 由点和边组成的集合。
- 有(无)向图 : 点与点之间状态的转移具有(没有)方向性。
- 连通 : 如果两个点之间相互可通过路径到达,则称两点连通。
- 连通分量 : 无向图中极大的任意两点相互连通的子图。
- 强连通分量 : 有向图中极大的任意两点相互连通的子图。
- (强)连通图 : 只有一个(强)连通分量的图。
- 树 : 无向无环图。
- \(DAG\) : 有向无环图。
Tarjan
概况
- 处理连通性问题的算法。
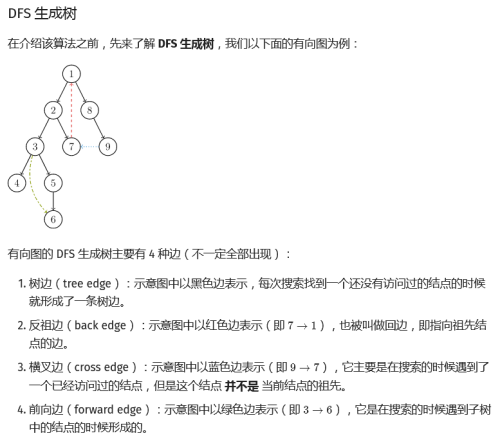
\(^{*}\) \(u\) 子树:即以 \(u\) 为根的子树。
过程
以求强连通分量为例。
Luogu P3387
给定一个 \(n\) 个点 \(m\) 条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。
容易发现,对于一个强连通分量内的点,我们可以看做一个点来处理,且权值等于其中所有点权值之和。
并且,如果我们按照强连通分量来缩点,我们将得到一个 \(DAG\),然后 \(DAG\) 上 \(Topo\) 求解最大权值路径。
我们来看其中的缩点部分。
如果结点 \(u\) 是某个强连通分量在搜索树中遇到的第一个结点,那么这个强连通分量的其余结点肯定是在搜索树中以 \(u\) 为根的子树中。结点 \(u\) 被称为这个强连通分量的根。
\(dfs\) 中途维护三个东西:
栈 : 被搜到却没有归属任何一个强连通分量的点。
\(dfn[u]\) : \(u\) 的 \(dfs\) 序。
\(low[u]\) : 从 \(u\) 出发能到达的栈中的点 \(dfn\) 的最小值。
过程:
对于 \(Tarjan(u)\),有如下过程 :
- 加入栈。
- 遍历每一条出边,对于下一个点 \(v\),有以下讨论 :
- 如果未搜到过, \(Tarjan(v)\), 并用 \(low[v]\) 更新 \(low[u]\) 。
- 如果搜到过,并且在栈中,用 \(dfn[v]\) 更新 \(low[u]\)。
- 否则不作处理。
- 如果 \(dfn[u] = low[u]\),即 \(u\) 为某一个强连通分量的根,则将此刻栈中 \(u\) 即其上的点全部划为一个强连通分量 \(scc\)。
反证法证明略。
\(scc\) 之间连边建新图跑 \(Topo\) 即可。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 1e4 + 7;
int n, m, scc, bel[_], stk[_], dfn[_], low[_], idx, val[_], _val[_], f[_], deg[_]; bool in[_];
int u, v, ans;
std::vector <int> e[_], _e[_];
void Tarjan(int u) {
low[u] = dfn[u] = ++idx, stk[++*stk] = u, in[u] = true;
for (int v : e[u]) {
if (!dfn[v]) Tarjan(v), low[u] = std::min(low[u], low[v]);
else if (in[v]) low[u] = std::min(low[u], dfn[v]);
}
if (low[u] == dfn[u]) { ++scc;
while (stk[*stk] != u) {
int nw = stk[(*stk)--]; in[nw] = false;
bel[nw] = scc, _val[scc] += val[nw];
}
--*stk, bel[u] = scc, _val[scc] += val[u], in[u] = false;
}
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, n) scanf("%d", val + i);
lep(i, 1, m) scanf("%d%d", & u, & v), e[u].push_back(v);
lep(i, 1, n) if (!dfn[i]) Tarjan(i);
lep(u, 1, n) for (int v : e[u]) if (bel[u] != bel[v]) _e[bel[u]].push_back(bel[v]), ++deg[bel[v]];
std::queue <int> d;
lep(i, 1, scc) if (!deg[i]) d.push(i);
while (!d.empty()) {
int u = d.front(); d.pop(); f[u] += _val[u]; ans = std::max(ans, f[u]);
for (int v : _e[u]) {
--deg[v], f[v] = std::max(f[v], f[u]);
if (!deg[v]) d.push(v);
}
}
printf("%d\n", ans);
return 0;
}
其他
边双连通分量
点击查看
可以发现相当于将无向图的边赋予一个方向后缩点。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u) for (int i = H[u], v = e[i].v; i ; i = e[i].n, v = e[i].v)
typedef long long ll;
const int _ = 5e5 + 7 ;
const int __ = 4e6 + 7;
struct edge { int v, n; } e[__]; int cnte = 1, H[_];
int n, m, low[_], dfn[_], idx, u, v, stk[_]; bool vis[__];
std::vector <std::vector<int> > Ans;
void A(int u, int v) { e[++cnte] = { v, H[u] }; H[u] = cnte; }
void Tarjan(int u) {
low[u] = dfn[u] = ++idx, stk[++*stk] = u;
ep(i, u) {
if (vis[i ^ 1]) continue; vis[i] = true;
if (!dfn[v]) Tarjan(v), low[u] = std::min(low[u], low[v]);
else low[u] = std::min(low[u], dfn[v]);
}
if (low[u] == dfn[u]) {
std::vector <int> x;
while (stk[*stk] != u) x.push_back(stk[(*stk)--]);
x.push_back(stk[(*stk)--]);
Ans.push_back(x);
}
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, m) scanf("%d%d", & u, & v), A(u, v), A(v, u);
lep(i, 1, n) if (!dfn[i]) Tarjan(i);
printf("%d\n", (int)Ans.size());
for (auto x : Ans) {
printf("%d\n", (int)x.size());
for (int i : x) printf("%d ", i);
putchar('\n');
}
return 0;
}
割点
点击查看
对于非根结点 \(u\),可以发现 \(u\) 是割点的充分条件是存在一个子结点 \(v\) 满足 low[v] >= dfn[u] 。
对于根节点 \(rt\),如果 \(rt\) 有多于一个子结点,那么 \(rt\) 是割点。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u) for (int i = H[u], v = e[i].v; i ; i = e[i].n, v = e[i].v)
const int _ = 2e4 + 7 ;
const int __ = 2e5 + 7;
struct edge { int v, n; } e[__]; int cnte = 1, H[_];
int n, m, low[_], dfn[_], idx, u, v, rt; bool vis[__], f[_];
void A(int u, int v) { e[++cnte] = { v, H[u] }; H[u] = cnte; }
void Tarjan(int u) { int son = 0;
low[u] = dfn[u] = ++idx;
ep(i, u) {
if (vis[i ^ 1]) continue; vis[i] = true;
if (!dfn[v]) {
++son, Tarjan(v), low[u] = std::min(low[u], low[v]);
if (low[v] >= dfn[u] and rt != u) f[u] = true;
}
else low[u] = std::min(low[u], dfn[v]);
}
if (son > 1 and rt == u) f[u] = true;
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, m) scanf("%d%d", & u, & v), A(u, v), A(v, u);
lep(i, 1, n) if (!dfn[i]) rt = i, Tarjan(i);
int tot = 0;
lep(i, 1, n) if (f[i]) ++tot;
printf("%d\n", tot);
lep(i, 1, n) if (f[i]) printf("%d ", i);
return 0;
}
点双连通分量
点击查看
割点将图分割成了若干个点双,统计即可。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u) for (int i = H[u], v = e[i].v; i ; i = e[i].n, v = e[i].v)
const int _ = 5e5 + 7 ;
const int __ = 4e6 + 7;
struct edge { int v, n; } e[__]; int cnte = 1, H[_];
int n, m, low[_], dfn[_], idx, u, v, rt, stk[_]; bool vis[__];
std::vector <std::vector<int> > Ans;
void A(int u, int v) { e[++cnte] = { v, H[u] }; H[u] = cnte; }
void Tarjan(int u) { int son = 0;
low[u] = dfn[u] = ++idx, stk[++*stk] = u;
ep(i, u) {
if (vis[i ^ 1]) continue; vis[i] = true;
if (!dfn[v]) {
++son, Tarjan(v), low[u] = std::min(low[u], low[v]);
if (low[v] >= dfn[u]) {
std::vector <int> x;
x.push_back(u);
while (stk[*stk] != v) x.push_back(stk[(*stk)--]);
x.push_back(stk[(*stk)--]);
Ans.push_back(x);
}
}
else low[u] = std::min(low[u], dfn[v]);
}
if (rt == u and !son) {
std::vector <int> x;
x.push_back(u);
Ans.push_back(x);
}
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, m) scanf("%d%d", & u, & v), A(u, v), A(v, u);
lep(i, 1, n) if (!dfn[i]) rt = i, Tarjan(i);
printf("%d\n", (int)Ans.size());
for (auto x : Ans) {
printf("%d ", (int)x.size());
for (int i : x) printf("%d ", i);
putchar('\n');
}
return 0;
}
例题
[USACO04DEC] Cow Ski Area G
罗恩的雪场可以划分为 \(W\) 列 \(L\) 行 \((1\le W\le 500, 1\le L\le 500)\),每个方格有一个特定的高度 \(H(0\le H\le 9999)\)。奶牛可以在相邻方格间滑雪,而且不能由低到高滑。
为了保证任意方格可以互通,罗恩打算造一些直达缆车。缆车很强大,可以连接任意两个方格,而且是双向的。而且同一个方格也可以造多台缆车。但是缆车的建造费用贵得吓人,所以他希望造尽量少的缆车。那最少需要造多少台呢?
点击查看
缩点得到一个 \(DAG\),可以证明使其变为一个强连通图的最小连边数为入度为 \(0\) 和出度为 \(0\) 的点个数较大值。
证明:
设入度为 \(0\) 的点有 \(n_1\) 个,出度为 \(0\) 的点有 \(n_2\) 个。
每个这样的点所在连通分量想要和其他点连通至少需要一条边,所以 \(ans \ge \max(n_1, n_2)\)
转换为二分图,设其最大匹配为 \(m\),则需要 \(m\) 条边就可以将匹配边连接的点变为一个强连通分量,称为中转部分。
剩下的结点两两之间没有边,给他们对应连上,这时候可能会有剩下的结点,和中转部分的点连边,可以发现这样构造 \(ans \le \max(n_1, n_2)\)。
所以, \(ans = \max(n_1, n_2)\)。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 1e6 + 7;
int w, l, a[501][501], stk[_], low[_], dfn[_], idx, bel[_], scc; bool in[_];
std::vector <int> e[_]; int In[_], Out[_];
int di[4] = { 1, -1, 0, 0 };
int dj[4] = { 0, 0, 1, -1 };
int id(int x, int y) { return (x - 1) * w + y; }
void Tarjan(int u) {
dfn[u] = low[u] = ++idx, stk[++*stk] = u, in[u] = true;
for (int v : e[u]) {
if (!dfn[v]) Tarjan(v), low[u] = std::min(low[u], low[v]);
else if (in[v]) low[u] = std::min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) { ++scc;
while (stk[*stk] != u) {
int nw = stk[(*stk)--];
in[nw] = false, bel[nw] = scc;
}
int nw = stk[(*stk)--];
in[nw] = false, bel[nw] = scc;
}
}
int main() {
scanf("%d%d", & w, & l);
lep(i, 1, l) lep(j, 1, w) scanf("%d", a[i] + j);
lep(i, 1, l) lep(j, 1, w) lep(k, 0, 3) {
int ni = i + di[k], nj = j + dj[k];
if (ni < 1 or ni > l or nj < 1 or nj > w or a[ni][nj] > a[i][j]) continue;
e[id(i, j)].push_back(id(ni, nj));
}
lep(i, 1, l * w) if (!dfn[i]) Tarjan(i);
lep(u, 1, l * w)
for (int v : e[u]) if (bel[u] != bel[v]) ++Out[bel[u]], ++In[bel[v]];
if (scc == 1) { puts("0"); return 0; }
int t1 = 0, t2 = 0;
lep(i, 1, scc) { if (!In[i]) ++t1; if (!Out[i]) ++t2; }
printf("%d\n", std::max(t1, t2));
return 0;
}
[国家集训队] 稳定婚姻
我们已知 \(n\) 对夫妻的婚姻状况,称第 \(i\) 对夫妻的男方为 \(B_i\),女方为 \(G_i\)。若某男 \(B_i\) 与某女 \(G_j\) 曾经交往过(无论是大学,高中,亦或是幼儿园阶段,\(i \le j\)),则当某方与其配偶(即 \(B_i\) 与 \(G_i\) 或 \(B_j\) 与 \(G_j\))感情出现问题时,他们有私奔的可能性。不妨设 \(B_i\) 和其配偶 \(G_i\) 感情不和,于是 \(B_i\) 和 \(G_j\) 旧情复燃,进而 \(B_j\) 因被戴绿帽而感到不爽,联系上了他的初恋情人 \(G_k\) ……一串串的离婚事件像多米诺骨牌一般接踵而至。若在 \(B_i\) 和 \(G_i\) 离婚的前提下,这 \(2n\) 个人最终依然能够结合成 \(n\) 对情侣,那么我们称婚姻 \(i\) 为不安全的,否则婚姻 \(i\) 就是安全的。
给定所需信息,你的任务是判断每对婚姻是否安全。
点击查看
容易发现重新组合的过程组成了一个环,建有向图找环。
在同一个强联通分量(不是边双联通分类)里的婚姻是不安全的。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u) for (int i = H[u], v = e[i].v; i ; i = e[i].n, v = e[i].v)
typedef std::string Str;
const int _ = 1e4 + 7 ;
const int __ = 1e5 + 7;
struct edge { int v, n; } e[__]; int cnte = 1, H[_];
int n, m, low[_], dfn[_], idx, rt, stk[_], scc, bel[_]; bool in[_];
std::map <Str, int> S; Str u[_], v[_]; int tot;
void A(int u, int v) { e[++cnte] = { v, H[u] }; H[u] = cnte; }
void Tarjan(int u) {
low[u] = dfn[u] = ++idx, stk[++*stk] = u, in[u] = true;
ep(i, u) {
if (!dfn[v]) Tarjan(v), low[u] = std::min(low[u], low[v]);
else if (in[v]) low[u] = std::min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) { ++scc;
while (stk[*stk] != u) { int nw = stk[(*stk)--]; in[nw] = false, bel[nw] = scc; }
int nw = stk[(*stk)--]; in[nw] = false, bel[nw] = scc;
}
}
int main() {
std::ios::sync_with_stdio(false),
std::cin.tie(nullptr), std::cout.tie(nullptr);
std::cin >> n;
lep(i, 1, n) {
std::cin >> u[i] >> v[i];
int l = S[u[i]] = ++tot, r = S[v[i]] = ++tot;
A(r, l);
}
std::cin >> m; Str a, b;
lep(i, 1, m)
std::cin >> a >> b, A(S[a], S[b]);
lep(i, 1, tot) if (!dfn[i]) Tarjan(i);
lep(i, 1, n) std::cout << (bel[S[u[i]]] == bel[S[v[i]]] ? "Unsafe\n" : "Safe\n");
return 0;
}
[POI2006] PRO-Professor Szu
某大学校内有一栋主楼,还有 \(n\) 栋住宅楼。这些楼之间由一些单向道路连接,但是任意两栋楼之间可能有多条道路,也可能存在起点和终点为同一栋楼的环路。存在住宅楼无法到达主楼的情况。
现在有一位古怪的教授,他希望每天去主楼上班的路线不同。
一条上班路线中,每栋楼都可以访问任意多次。我们称两条上班路线是不同的,当且仅当两条路线中存在一条路是不同的(两栋楼之间的多条道路被视为是不同的道路)。
现在教授希望知道,从哪些住宅楼前往主楼的上班路线数最多。
点击查看
倒序建图 \(+\) 缩点 \(+\) \(Topu\)
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
const int _ = 1e6 + 7;
const int inf = 36501;
int n, m, low[_], dfn[_], idx, stk[_], bel[_], scc;
int f[_], In[_], u[_], v[_]; bool vis[_];
std::vector <int> e[_], E[_];
void Tarjan(int u) {
low[u] = dfn[u] = ++idx, stk[++*stk] = u, In[u] = true;
for (int v : e[u]) {
if (!dfn[v]) Tarjan(v), low[u] = std::min(low[u], low[v]);
else if (In[v]) low[u] = std::min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) { ++scc; int tot = 0;
while (stk[*stk] != u) {
int nw = stk[(*stk)--]; ++tot, bel[nw] = scc, In[nw] = false;
}
int nw = stk[(*stk)--]; ++tot, In[nw] = false, bel[nw] = scc;
if (tot > 1) vis[scc] = true;
}
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, m) scanf("%d%d", v + i, u + i), e[u[i]].push_back(v[i]);
lep(i, 1, n + 1) if (!dfn[i]) Tarjan(i);
std::memset(In, 0, sizeof(In));
std::queue <int> d;
lep(i, 1, m) {
if (u[i] == v[i]) vis[bel[u[i]]] = true;
if (bel[u[i]] != bel[v[i]]) E[bel[u[i]]].push_back(bel[v[i]]), ++In[bel[v[i]]];
}
lep(i, 1, n + 1) if (!In[i]) d.push(i);
int ans = 0, sum = 0;
f[bel[n + 1]] = 1;
while (!d.empty()) {
int u = d.front(); d.pop();
if (vis[u] and f[u]) f[u] = inf;
if (f[u] > ans) ans = f[u];
for (int v : E[u]) {
f[v] = std::min(inf, f[v] + f[u]), --In[v];
if (!In[v]) d.push(v);
}
}
if (ans == inf) puts("zawsze");
else printf("%d\n", ans);
std::memset(vis, 0, sizeof(vis));
lep(i, 1, scc) if (f[i] == ans) vis[i] = true;
lep(i, 1, n) if (vis[bel[i]]) ++sum;
printf("%d\n", sum);
lep(i, 1, n) if (vis[bel[i]]) printf("%d ", i);
return 0;
}
[POI2012] FES-Festival
Byteasar 告诉你,所有参赛者的成绩都是整数秒。他还会为你提供了一些参赛者成绩的关系。具体是:他会给你一些数对 \((A, B)\),表示 \(A\) 的成绩正好比 \(B\) 快 \(1\) 秒;他还会给你一些数对 \((C, D)\),表示 \(C\) 的成绩不比 \(D\) 慢。而你要回答的是:所有参赛者最多能达到多少种不同的成绩,而不违背他给的条件。
\(\texttt{Full_Speed 版题面:}\)
\(n\) 个带权点,赋予它们各一个正整数权值,使得满足两类限制。
1 u v: \(val_u = val_v - 1\)2 u v: \(val_u \le val_v\)
求最多有多少种不同的点权。
点击查看
用差分约束建图,对于其中的两个点 \(u\) 、\(v\) ,可以发现只有当它们强连通时,选择的值域才有上下界差值的限制。
对于一个强连通分量中的点,其贡献为 最长路长度 \(+ 1\)。
且多个强连通分量之间不会相互影响,因为它们要么不相连,要么有权为 \(0\) 的边,可以通过将值域拉开很远来解决。
所以最终答案就是将各个强连通分量的贡献累加。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
typedef long long ll;
const int _ = 600 + 7;
const int __ = 2e5 + 7;
const int inf = 100000;
int n, m1, m2, dis[_][_], low[_], dfn[_], idx, bel[_], stk[_], scc, nw, p[_], ans; bool in[_];
void Tarjan(int u) {
low[u] = dfn[u] = ++idx, stk[++*stk] = u, in[u] = true;
lep(v, 1, n) if (dis[u][v] != inf and u != v) {
if (!dfn[v]) Tarjan(v), low[u] = std::min(low[u], low[v]);
else if (in[v]) low[u] = std::min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) { ++scc;
while (stk[*stk] != u) { nw = stk[(*stk)--]; bel[nw] = scc, in[nw] = false; }
nw = stk[(*stk)--]; bel[nw] = scc, in[nw] = false;
}
}
int main() {
scanf("%d%d%d", & n, & m1, & m2);
lep(i, 1, n) { lep(j, 1, n) if (i != j) dis[i][j] = inf; p[i] = i; }
int u, v;
lep(i, 1, m1) {
scanf("%d%d", & u, & v);
dis[u][v] = std::min(dis[u][v], -1), dis[v][u] = std::min(dis[v][u], 1);
}
lep(i, 1, m2) {
scanf("%d%d", & u, & v);
dis[u][v] = std::min(dis[u][v], 0);
}
lep(i, 1, n) if (!dfn[i]) Tarjan(i);
std::sort(p + 1, p + 1 + n, [](int x, int y) { return bel[x] < bel[y]; });
int lst = 1, pos = 1;
while (lst <= n) {
while (bel[p[pos]] == bel[p[lst]]) ++pos;
lep(k, lst, pos - 1) lep(i, lst, pos - 1) lep(j, lst, pos - 1) dis[p[i]][p[j]] = std::min(dis[p[i]][p[j]], dis[p[i]][p[k]] + dis[p[k]][p[j]]);
int mx = 0;
lep(i, lst, pos - 1) {
if (dis[p[i]][p[i]] < 0) goto Nie;
lep(j, lst, pos - 1) mx = std::max(dis[p[i]][p[j]] + 1, mx);
}
ans += mx, lst = pos;
}
printf("%d\n", ans);
return 0;
Nie:
puts("NIE");
return 0;
}
[HNOI2012] 矿场搭建
煤矿工地可以看成是由隧道连接挖煤点组成的无向图。为安全起见,希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。于是矿主决定在某些挖煤点设立救援出口,使得无论哪一个挖煤点坍塌之后,其他挖煤点的工人都有一条道路通向救援出口。
请写一个程序,用来计算至少需要设置几个救援出口,以及不同最少救援出口的设置方案总数。
点击查看
求点双后分讨,对于一个点双:
如果没有割点,标记其中两个点,当然如果只有一个孤立点就标记一个点。
如果有一个割点,标记除割点外的一个点。
如果有多余(包含)两个割点,则不需标记,因为可以通过没有被堵住的割点去别的点双。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u) for (int i = H[u], v = e[i].v; i ; i = e[i].n, v = e[i].v)
typedef long long ll;
const int _ = 2e5 + 7;
struct edge { int v, n; } e[_]; int H[_], cnte = 1; bool vis[_];
int n, m, rt, stk[_]; bool f[_];
int dfn[_], low[_], idx;
std::vector <std::vector <int> > SCC;
void A(int u, int v) { e[++cnte] = { v, H[u] }, H[u] = cnte; }
void Tarjan(int u) { int son = 0;
dfn[u] = low[u] = ++idx, stk[++*stk] = u;
ep(i, u) {
if (vis[i ^ 1]) continue; vis[i] = true;
if (!dfn[v]) {
Tarjan(v), low[u] = std::min(low[u], low[v]), ++son;
if (low[v] >= dfn[u]) { int nw;
if (rt != u) f[u] = true;
std::vector <int> x;
x.push_back(u);
while (stk[*stk] != u)
x.push_back(stk[(*stk)--]);
SCC.push_back(x);
}
}
else low[u] = std::min(low[u], dfn[v]);
}
if (rt == u and son > 1) f[u] = true;
}
void C() {
lep(i, 1, n) f[i] = dfn[i] = low[i] = H[i] = 0; n = idx = *stk = 0;
lep(i, 1, cnte) vis[i] = false;
SCC.clear();
cnte = 1;
}
int main() { int T = 0;
while (++T) {
scanf("%d", & m); int u, v;
if (!m) break;
lep(i, 1, m) scanf("%d%d", & u, & v), A(u, v), A(v, u), n = std::max(n, std::max(u, v));
lep(u, 1, n) if (!dfn[u]) rt = u, Tarjan(u);
ll ans = 0, tot = 1;
for (auto x : SCC) { ll len = x.size(), u, tmp = 0;
for (int i : x)
if (f[i]) ++tmp, u = i;
if (tmp == 1) ++ans, tot *= len - 1;
else if (!tmp) ans += 2, tot *= n * (n - 1) / 2;
}
printf("Case %d: %lld %lld\n", T, ans, tot);
C();
}
return 0;
}
[NOIP2022] 建造军营
A 国的国土由 \(n\) 座城市组成,\(m\) 条双向道路连接这些城市,使得任意两座城市均可通过道路直接或间接到达。A 国打算选择一座或多座城市(至少一座),并在这些城市上各建造一座军营。
众所周知,军营之间的联络是十分重要的。然而此时 A 国接到情报,B 国将会于不久后袭击 A 国的一条道路,但具体的袭击目标却无从得知。如果 B 国袭击成功,这条道路将被切断,可能会造成 A 国某两个军营无法互相到达,这是 A 国极力避免的。因此 A 国决定派兵看守若干条道路(可以是一条或多条,也可以一条也不看守),A 国有信心保证被派兵看守的道路能够抵御 B 国的袭击而不被切断。
A 国希望制定一个建造军营和看守道路的方案,使得 B 国袭击的无论是 A 国的哪条道路,都不会造成某两座军营无法互相到达。现在,请你帮 A 国计算一下可能的建造军营和看守道路的方案数共有多少。由于方案数可能会很多,你只需要输出其对 \(1,000,000,007\left(10^{9}+7\right)\) 取模的值即可。两个方案被认为是不同的,当且仅当存在至少一 座城市在一个方案中建造了军营而在另一个方案中没有,或者存在至少一条道路在一个 方案中被派兵看守而在另一个方案中没有。
点击查看
发现割掉桥之外的边没有影响。
将原图缩成一棵树后 \(DP\) 。
在所有标记点的 \(LCA\) 处统计答案,且强制要求 \(fa_u\) 与 \(u\) 之间的边不选,如果不存在则不要求。
记 \(dp[u][0/1]\) 为 \(u\) 子树内没有 / 有标记点的方案数,如果有标记点,要求所有标记点都通过标记边与 \(u\) 联通。
具体的可以自己推一推,然后看代码。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u) for (int i = H[u], v = e[i].v; i; i = e[i].n, v = e[i].v)
typedef long long ll;
const int _ = 2e6 + 7;
const int mod = 1e9 + 7;
struct Edge { int v, n; }e[_]; int cnte = 1, H[_]; bool vis[_];
int n, m, u[_], v[_]; int idx, dfn[_], low[_], stk[_], bel[_], V[_], scc;
ll dp[_][2], ans, siz[_];
std::vector <int> to[_];
ll MyPow(ll a, ll b) {
ll ans = 1;
for (; b; b >>= 1, a = a * a % mod)
if (b & 1) ans = ans * a % mod;
return ans;
}
void Add_Edge(int u, int v) { e[++cnte] = { v, H[u] }, H[u] = cnte; }
void Tarjan(int u) {
dfn[u] = low[u] = ++idx; stk[++*stk] = u;
ep(i, u) {
if (vis[i ^ 1]) continue; vis[i] = true;
if (!dfn[v]) Tarjan(v), low[u] = std::min(low[u], low[v]);
else low[u] = std::min(low[u], dfn[v]);
}
if (low[u] == dfn[u]) { int nw; ++scc;
while (stk[*stk] != u) {
nw = stk[(*stk)--];
bel[nw] = scc, ++V[scc];
}
nw = stk[(*stk)--];
bel[nw] = scc, ++V[scc];
}
}
void Dfs(int u, int f) {
dp[u][0] = 1, dp[u][1] = MyPow(2, V[u]) - 1, siz[u] = 1;
for (int v : to[u]) if (v != f) {
Dfs(v, u), siz[u] += siz[v];
dp[u][1] = (dp[u][0] * dp[v][1] % mod + dp[u][1] * (dp[v][0] * 2 + dp[v][1]) % mod) % mod;
dp[u][0] = dp[u][0] * dp[v][0] * 2 % mod;
}
if (u == 1) ans = (ans + dp[u][1]) % mod;
else ans = (ans + MyPow(2, scc - 1 - siz[u]) * dp[u][1] % mod) % mod;
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, m) scanf("%d%d", u + i, v + i),
Add_Edge(u[i], v[i]), Add_Edge(v[i], u[i]);
Tarjan(1);
lep(i, 1, m) {
if (bel[u[i]] != bel[v[i]])
to[bel[u[i]]].push_back(bel[v[i]]),
to[bel[v[i]]].push_back(bel[u[i]]);
}
Dfs(1, 0);
ans = MyPow(2, m - scc + 1) * ans % mod;
printf("%lld\n", ans);
return 0;
}
边三连通分量
对于一张无向图 \(G = (V, E)\)。
- 我们称两个点 \(u, v ~ (u, v \in V, u \neq v)\) 是边三连通的,当且仅当存在三条从 \(u\) 出发到达 \(v\) 的,相互没有公共边的路径。
- 我们称一个点集 \(U ~ (U \subseteq V)\) 是边三连通分量,当且仅当对于任意两个点 \(u', v' ~ (u', v' \in U, u' \neq v')\) 都是边三连通的。
- 我们称一个边三连通分量 \(S\) 是极大边三连通分量,当且仅当不存在 \(u \not \in S\) 且 \(u \in V\),使得 \(S \cup \{u\}\) 也是边三连通分量。
点击查看
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, d) for (int i = H[u], d = e[i].v; i; i = e[i].n, d = e[i].v)
typedef unsigned long long ull;
const int _ = 5e6 + 7;
struct Edge { int v, n; } e[_]; int cnte = 1, H[_];
int n, m, fa[_]; ull val[_];
int dfn[_], dfn1[_], low[_], idx; bool ct[_], ot[_], ct1[_];
std::set <ull> S;
std::map <ull, int> T;
std::vector <std::vector<int> > Ans;
int rd() { return (std::rand() << 14) | std::rand(); }
void AddE(int u, int v) { e[++cnte] = { v, H[u] }, H[u] = cnte; }
void Tarjan(int u, int f = 0) {
dfn[u] = low[u] = ++idx;
ep(i, u, v) {
if (i == f) continue;
if (!dfn[v]) {
Tarjan(v, i ^ 1), low[u] = std::min(low[u], low[v]);
if (low[v] == dfn[v]) ct[i] = ct[i ^ 1] = true;
}
else low[u] = std::min(low[u], dfn[v]);
}
}
void Dfs3(int u, int ed, std::vector <int>& res) {
res.push_back(u);
ep(i, u, v) {
if (v == ed or ct[i] or ct1[i] or !ot[i]) continue;
Dfs3(v, ed, res);
}
}
void Dfs2(int u, int f = 0) {
ep(i, u, v) {
if (ct[i] or ct1[i] or !ot[i]) continue;
Dfs2(v, i);
}
if (T.count(val[u])) {
int v = T[val[u]];
std::vector <int> res;
Dfs3(u, v, res);
Ans.push_back(res);
ot[f] = false;
AddE(fa[u], v), fa[v] = fa[u];
ot[cnte] = true;
T[val[u]] = v;
}
else T[val[u]] = u;
}
void Dfs1(int u, int f = 0) {
dfn1[u] = ++idx;
ep(i, u, v) {
if (i == (f ^ 1) or ct[i]) continue;
if (!dfn1[v]) {
ot[i] = true, fa[v] = u;
Dfs1(v, i);
val[u] ^= val[v];
}
else {
if (dfn1[v] > dfn1[u]) continue;
ull w = rd();
S.insert(w);
val[u] ^= w, val[v] ^= w;
}
}
if (S.count(val[u])) ct1[f] = ct1[f ^ 1] = true;
if (!f or ct1[f]) {
T.clear();
Dfs2(u);
std::vector <int> res;
Dfs3(u, 0, res);
Ans.push_back(res);
}
}
int main() {
std::srand(time(0));
scanf("%d%d", & n, & m); int a, b;
lep(i, 1, m) {
scanf("%d%d", & a, & b);
AddE(a, b), AddE(b, a);
}
lep(i, 1, n) if (!dfn[i]) Tarjan(i);
idx = 0;
lep(i, 1, n) if (!dfn1[i]) Dfs1(i);
for (auto& t : Ans) std::sort(t.begin(), t.end());
std::sort(Ans.begin(), Ans.end());
printf("%d\n", (int)Ans.size());
for (auto t : Ans) {
for (int i : t) printf("%d ", i);
puts("");
}
return 0;
}
圆方树
简述
将每一个点双缩成一个方点,向点双内的每一个点(称作圆点)连一条边,建一个 \(n + scc\) 个点的新图,称作圆方树。
容易发现,一条边的两个端点一定是一个方点,一个圆点。
并且非割点的圆点度数为 \(1\) 。
我们用圆方树来刻画原图的 必经性 和 可经性 。
对于原图两点 \((u, v)\) ,有:
- \(u\) 到 \(v\) 的所有简单路径的交即为圆方树上路径的所有圆点。
- \(u\) 到 \(v\) 的所有简单路径的并即为圆方树上路径的所有方点所代表的点双。
下面来看几个例题来理解这种性质。
例题
道路相遇
在 \(H\) 国的小 \(w\) 决定到从城市 \(u\) 到城市 \(v\) 旅行,但是此时小 \(c\) 由于各种原因不在城市 \(u\),但是小 \(c\) 决定到在中途与小 \(w\) 相遇
由于 \(H\) 国道路的原因,小 \(w\) 从城市 \(u\) 到城市 \(v\) 的路线不是固定的,为了合理分配时间,小 \(c\) 想知道从城市 \(u\) 到城市 \(v\) 有多少个城市小 \(w\) 一定会经过,特别地,\(u, v\) 也必须被算进去,也就是说无论如何答案不会小于 \(2\) 。
由于各种特殊的原因,小 \(c\) 并不知道小 \(w\) 的起点和终点,但是小 \(c\) 知道小 \(w\) 的起点和终点只有 \(q\) 种可能,所以对于这 \(q\) 种可能,小 \(c\) 都想知道小 \(w\) 一定会经过的城市数
\(H\) 国所有的边都是无向边,两个城市之间最多只有一条道路直接相连,没有一条道路连接相同的一个城市
任何时候,\(H\) 国不存在城市 \(u\) 和城市 \(v\) 满足从 \(u\) 无法到达 \(v\)
点击查看
可以发现题目要求的即为两点之间的割点个数。
建圆方树,所有圆点赋值为 \(1\), 问题即为两点之间的路径权值和,树剖即可。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
typedef long long ll;
const int _ = 2e6 + 7;
struct Edge { int v, n; }e[_]; int cnte = 1, H[_];
int n, m, q;
int scc, stk[_], dfn[_], low[_], idx;
int dep[_], fa[_], son[_], top[_], siz[_];
int c[_];
std::vector <int> e1[_];
void AddEdge(int u, int v) { e[++cnte] = Edge { v, H[u] }, H[u] = cnte; }
void Add(int u, int v) { e1[u].push_back(v), e1[v].push_back(u); }
void Tarjan(int u) {
dfn[u] = low[u] = ++idx, stk[++*stk] = u;
for (int i = H[u], v = e[i].v; i ; i = e[i].n, v = e[i].v) {
if (!dfn[v]) {
Tarjan(v);
low[u] = std::min(low[u], low[v]);
if (low[v] == dfn[u]) {
++scc; int nw;
Add(u, n + scc);
while (stk[*stk] != v) {
nw = stk[(*stk)--];
Add(nw, n + scc);
}
nw = stk[(*stk)--];
Add(nw, n + scc);
}
}
else low[u] = std::min(low[u], dfn[v]);
}
}
void Add(int x) { while (x <= n + scc) ++c[x], x += x & -x; }
int Get(int x) { int res = 0; while (x) res += c[x], x -= x & -x; return res; }
int Gets(int l, int r) { return Get(r) - Get(l - 1); }
void Dfs1(int u, int f) {
dep[u] = dep[fa[u] = f] + 1; siz[u] = 1;
for (int v : e1[u]) if (v != f) {
Dfs1(v, u); siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
void Dfs2(int u, int t) {
top[u] = t, dfn[u] = ++idx;
if (u <= n) Add(dfn[u]);
if (!son[u]) return;
Dfs2(son[u], t);
for (int v : e1[u]) if (v != fa[u] and v != son[u]) {
Dfs2(v, v);
}
}
int Query(int x, int y) {
int res = 0;
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
res += Gets(dfn[top[x]], dfn[x]);
x = fa[top[x]];
}
if (dep[x] > dep[y]) std::swap(x, y);
res += Gets(dfn[x], dfn[y]);
return res;
}
int main() {
scanf("%d%d", & n, & m); int u, v;
lep(i, 1, m)
scanf("%d%d", & u, & v),
AddEdge(u, v), AddEdge(v, u);
Tarjan(1); idx = 0;
Dfs1(1, 0), Dfs2(1, 1);
scanf("%d", & q);
while (q--) {
scanf("%d%d", & u, & v);
printf("%d\n", Query(u, v));
}
return 0;
}
[SDOI2018] 战略游戏
省选临近,放飞自我的小 \(Q\) 无心刷题,于是怂恿小 \(C\) 和他一起颓废,玩起了一款战略游戏。
这款战略游戏的地图由 \(n\) 个城市以及 \(m\) 条连接这些城市的双向道路构成,并且从任意一个城市出发总能沿着道路走到任意其他城市。
现在小 \(C\) 已经占领了其中至少两个城市,小 \(Q\) 可以摧毁一个小 \(C\) 没占领的城市,同时摧毁所有连接这个城市的道路。只要在摧毁这个城市之后能够找到某两个小 \(C\) 占领的城市 \(u\) 和 \(v\),使得从 \(u\) 出发沿着道路无论如何都不能走到 \(v\),那么小 \(Q\) 就能赢下这一局游戏。
小 \(Q\) 和小 \(C\) 一共进行了 \(q\) 局游戏,每一局游戏会给出小 \(C\) 占领的城市集合 \(S\),你需要帮小 \(Q\) 数出有多少个城市在他摧毁之后能够让他赢下这一局游戏。
点击查看
圆方树上包含所有标记点的最小连通块中非关键点的圆点个数。
最小连通块,想到运用 \(dfs\) 序的常见 trick。
按照 \(dfs\) 序排序,维护边的条数,最后考虑 \(LCA\) 处的答案。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
typedef long long ll;
const int _ = 2e6 + 7;
struct Edge { int v, n; }e[_]; int cnte = 1, H[_];
int T, n, m, q, S[_];
int scc, stk[_], dfn[_], low[_], idx;
int dep[_], fa[_], son[_], top[_], siz[_];
int c[_], ans;
std::vector <int> e1[_];
void AddEdge(int u, int v) { e[++cnte] = Edge { v, H[u] }, H[u] = cnte; }
void Add(int u, int v) { e1[u].push_back(v), e1[v].push_back(u); }
void Tarjan(int u) {
dfn[u] = low[u] = ++idx, stk[++*stk] = u;
for (int i = H[u], v = e[i].v; i ; i = e[i].n, v = e[i].v) {
if (!dfn[v]) {
Tarjan(v);
low[u] = std::min(low[u], low[v]);
if (low[v] == dfn[u]) {
++scc; int nw;
Add(u, n + scc);
while (stk[*stk] != v) {
nw = stk[(*stk)--];
Add(nw, n + scc);
}
nw = stk[(*stk)--];
Add(nw, n + scc);
}
}
else low[u] = std::min(low[u], dfn[v]);
}
}
void Add(int x) { while (x <= n + scc) ++c[x], x += x & -x; }
int Get(int x) { int res = 0; while (x) res += c[x], x -= x & -x; return res; }
int Gets(int l, int r) { return Get(r) - Get(l - 1); }
void Dfs1(int u, int f) {
dep[u] = dep[fa[u] = f] + 1; siz[u] = 1;
for (int v : e1[u]) if (v != f) {
Dfs1(v, u); siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
void Dfs2(int u, int t) {
top[u] = t, dfn[u] = ++idx;
if (u <= n) Add(dfn[u]);
if (!son[u]) return;
Dfs2(son[u], t);
for (int v : e1[u]) if (v != fa[u] and v != son[u]) {
Dfs2(v, v);
}
}
int Query(int x, int y) {
int res = 0;
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
res += Gets(dfn[top[x]], dfn[x]);
x = fa[top[x]];
}
if (dep[x] > dep[y]) std::swap(x, y);
res += Gets(dfn[x] + 1, dfn[y]);
return res;
}
int IF(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
x = fa[top[x]];
}
if (dep[x] > dep[y]) std::swap(x, y);
return (x <= n);
}
int main() {
scanf("%d", & T);
while (T--) {
scanf("%d%d", & n, & m); int u, v;
lep(i, 1, m)
scanf("%d%d", & u, & v),
AddEdge(u, v), AddEdge(v, u);
Tarjan(1); idx = 0;
Dfs1(1, 0), Dfs2(1, 1);
scanf("%d", & q);
while (q--) {
scanf("%d", S);
lep(i, 1, *S) scanf("%d", S + i);
std::sort(S + 1, S + 1 + *S, [](int x, int y) { return dfn[x] < dfn[y]; });
lep(i, 1, *S) ans += Query(S[i], S[i % (*S) + 1]);
ans = ans / 2 - *S + IF(S[1], S[*S]);
printf("%d\n", ans); ans = 0;
}
lep(i, 1, n + scc) c[i] = H[i] = dfn[i] = low[i] = son[i] = 0, e1[i].clear();
idx = scc = 0; cnte = 1;
}
return 0;
}
[COI 2007] Policija
警察常常要抓住那些逃往另一个城市的罪犯。侦查员看着地图,试着确定在哪里设置路障。新的计算机系统要回答以下两种问题:
考虑城市 \(A\) 和 \(B\),以及连接城市 \(G_1\) 和 \(G_2\) 的道路。罪犯能否在那条路不通的情况下从 \(A\) 逃到 \(B\)?
考虑三个城市 \(A, B, C\)。罪犯能否在无法通过 \(C\) 的情况下从 \(A\) 逃到 \(B\)?
点击查看
建出圆方树,第二种询问即判断某点是否在两点之间路径上。
第一种询问即判断是否为割边(此边所在点双方点出度是否为 \(2\)),然后判断这个方点是否在两点之间路径上。
此题卡空间。
具体实现的时候需要找到代表一条边所属点双的方点。
另外维护一个边的栈,在加入点之后顺便加入边,最后把边都弹出来更新信息。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, d) for (int i = H[u], d = e[i].v; i; i = e[i].n, d = e[i].v)
typedef long long ll;
typedef std::pair<int, int> PII;
const int _ = 1.8e5 + 7;
struct Edge { int u, v, n; }e[_ * 10]; int H[_], cnte = 1;
int n, m, Q;
int dfn[_], low[_], idx, stk[_], scc, stke[_ * 10]; bool in[_];
int dep[_], son[_], top[_], fa[_], siz[_];
std::map<PII, int> Fro;
std::vector <int> e1[_];
void AddE(int u, int v) { e[++cnte] = { u, v, H[u]}, H[u] = cnte; }
void AE(int u, int v) { e1[u].push_back(v), e1[v].push_back(u); }
bool Check(int i, int u, int v) { return e[i].u == u and e[i].v == v; }
void Tarjan(int u, int f = 0) {
dfn[u] = low[u] = ++idx, stk[++*stk] = u; in[u] = true;
if (f) stke[++*stke] = f;
ep(i, u, v) {
if (!dfn[v]) {
Tarjan(v, i), low[u] = std::min(low[u], low[v]);
if (low[v] >= dfn[u]) {
int p = *stk, nw; ++scc;
while (stk[p] != v) --p;
while (!Check(stke[*stke], u, v)) {
nw = stke[(*stke)--];
Fro[std::minmax(e[nw].u, e[nw].v)] = scc;
}
nw = stke[(*stke)--];
Fro[std::minmax(e[nw].u, e[nw].v)] = scc;
rep(i, *stk, p) in[stk[i]] = false, AE(stk[i], n + scc);
AE(u, n + scc);
*stk = p - 1;
}
}
else {
if (in[v]) stke[++*stke] = i;
low[u] = std::min(low[u], dfn[v]);
}
}
}
void Dfs1(int u, int f) {
dep[u] = dep[fa[u] = f] + 1, siz[u] = 1;
for (int v : e1[u]) if (v != f) {
Dfs1(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
void Dfs2(int u, int tp) {
dfn[u] = ++idx, top[u] = tp;
if (!son[u]) return;
Dfs2(son[u], tp);
for (int v : e1[u]) if (v != fa[u] and v != son[u])
Dfs2(v, v);
}
bool Query(int x, int y, int c) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
if (top[x] == top[c] and dep[top[x]] <= dep[c]
and dep[c] <= dep[x]) return false;
x = fa[top[x]];
}
if (dep[x] > dep[y]) std::swap(x, y);
if (top[x] == top[c] and dep[x] <= dep[c] and dep[c] <= dep[y]) return false;
return true;
}
int main() {
scanf("%d%d", & n, & m); int u, v;
lep(i, 1, m) scanf("%d%d", & u, & v),
AddE(u, v), AddE(v, u);
Tarjan(1); idx = 0;
Dfs1(1, 0); Dfs2(1, 1);
int op, a, b, c, g1, g2;
scanf("%d", & Q);
while (Q--) {
scanf("%d", & op);
if (op == 1) {
scanf("%d%d%d%d", & a, & b, & g1, & g2);
int nd = Fro[std::minmax(g1, g2)] + n;
if (e1[nd].size() > 2) puts("yes");
else puts(Query(a, b, nd) ? "yes" : "no");
}
else {
scanf("%d%d%d", & a, & b, & c);
puts(Query(a, b, c) ? "yes" : "no");
}
}
return 0;
}
CF1763F Edge Queries
给定一张 \(n\) 个点 \(m\) 条边的无向图,满足对于所有的点 \(u\) ,
包含 u 的最长简单环与所有包含 u 的环的并集两个集合相同。
共 \(q\) 次询问,每次给定两个点 \(a,b\) ,求在所有能够出现在 \(a→b\) 简单路径中的边中,有多少条满足删掉之后 \(a,b\) 仍然连通。
点此查看
维护每个点双内有多少条边,如果只有一条,则为割边。
将非割边的点双权值赋为其中边的条数,求两点之间路径和。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
typedef long long ll;
const int _ = 4e5 + 7;
struct Edge { int u, v, n; }e[_]; int cnte = 1, H[_];
int T, n, m, q;
int scc, stk[_], dfn[_], low[_], idx, stke[_];
int dep[_], fa[_], son[_], top[_], siz[_]; bool in[_];
int c[_], ans, val[_];
std::set <std::pair<int, int>> Fro;
std::vector <int> e1[_];
void AddEdge(int u, int v) { e[++cnte] = Edge { u, v, H[u] }, H[u] = cnte; }
void Ae(int u, int v) { e1[u].push_back(v), e1[v].push_back(u); }
bool Check(int i, int u, int v) { return e[i].u == u and e[i].v == v; }
void Tarjan(int u, int f = 0) {
dfn[u] = low[u] = ++idx, stk[++*stk] = u; in[u] = true;
if (f) stke[++*stke] = f;
for (int i = H[u], v = e[i].v; i ; i = e[i].n, v = e[i].v) {
if (!dfn[v]) {
Tarjan(v, i);
low[u] = std::min(low[u], low[v]);
if (low[v] == dfn[u]) {
++scc; int nw;
Ae(u, n + scc);
while (stk[*stk] != v) {
nw = stk[(*stk)--], in[nw] = false;
Ae(nw, n + scc);
}
nw = stk[(*stk)--], in[nw] = false;
Ae(nw, n + scc);
while (!Check(stke[*stke], u, v)) {
nw = stke[(*stke)--];
Fro.insert(std::minmax(e[nw].u, e[nw].v));
}
nw = stke[(*stke)--];
Fro.insert(std::minmax(e[nw].u, e[nw].v));
val[n + scc] = Fro.size(); Fro.clear();
if (val[n + scc] == 1) val[n + scc] = 0;
}
}
else {
if (in[v]) stke[++*stke] = i;
low[u] = std::min(low[u], dfn[v]);
}
}
}
void Add(int x, int k) { while (x <= n + scc) c[x] += k, x += x & -x; }
int Get(int x) { int res = 0; while (x) res += c[x], x -= x & -x; return res; }
int Gets(int l, int r) { return Get(r) - Get(l - 1); }
void Dfs1(int u, int f) {
dep[u] = dep[fa[u] = f] + 1; siz[u] = 1;
for (int v : e1[u]) if (v != f) {
Dfs1(v, u); siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
void Dfs2(int u, int t) {
top[u] = t, dfn[u] = ++idx;
if (u > n) Add(dfn[u], val[u]);
if (!son[u]) return;
Dfs2(son[u], t);
for (int v : e1[u]) if (v != fa[u] and v != son[u]) {
Dfs2(v, v);
}
}
int Query(int x, int y) {
int res = 0;
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
res += Gets(dfn[top[x]], dfn[x]);
x = fa[top[x]];
}
if (dep[x] > dep[y]) std::swap(x, y);
res += Gets(dfn[x], dfn[y]);
return res;
}
int main() {
scanf("%d%d", & n, & m); int u, v;
lep(i, 1, m)
scanf("%d%d", & u, & v),
AddEdge(u, v), AddEdge(v, u);
Tarjan(1); idx = 0;
Dfs1(1, 0), Dfs2(1, 1);
scanf("%d", & q);
while (q--) {
scanf("%d%d", & u, & v);
printf("%d\n", Query(u, v));
}
return 0;
}
「SWTR-8」地地铁铁
给定一张 \(n\) 个点,\(m\) 条边的无向连通图。每条边标有
D或d。
定义无序点对 \((x, y)\) 是「铁的」,当且仅当 \(x \neq y\) 且 \(x, y\) 之间存在同时出现D和d的简单路径。
小 \(A\) 深知自由组合定律DdTt的重要性,所以他让你对这样的点对计数。
注意:
- 简单路径定义为不经过重复 节点 的路径。
- 保证图无自环,可能有重边。
点此查看
自由组合定律好题。
容斥,考虑只能经过全 \(0\) 边和全 \(1\) 边的点对。
不在一个点双内的,只要他们之间经过了不同颜色的点双,就不合法,并查集维护连通块大小。
在一个点双内的,我们发现最多只有一对这样的点对(呈杏仁状)。
并且这个 “杏仁” 等价于点双内有且仅有两个点出边既有 \(0\) , 又有 \(1\) 。
处理点双内都有什么颜色的边和上一题类似。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, d) for (int i = H[u], d = e[i].v; i; i = e[i].n, d = e[i].v)
typedef long long ll;
const int _ = 2e6 + 7;
struct Edge { int u, v, n, w; } e[_]; int cnte = 1, H[_];
int n, m, dp[_][2], fa[2][_], tot[2][_]; ll ans; bool in[_];
int dfn[_], low[_], stk[_], stke[_], col[_], idx, scc;
std::vector <int> e1[_];
int read() {
int x = 0; char c = getchar();
while (c < '0' or c > '9') c = getchar();
while (c >= '0' and c <= '9') x = x * 10 + c - '0', c = getchar();
return x;
}
void AddE(int u, int v, int w) { e[++cnte] = { u, v, H[u], w }, H[u] = cnte; }
void Ae(int u, int v) { e1[u].push_back(v), e1[v].push_back(u); }
inline void Qy(int c, int nd) {
if (!c) {
if (col[nd] == 0) col[nd] = 1;
if (col[nd] == 2) col[nd] = 3;
}
else {
if (col[nd] == 0) col[nd] = 2;
if (col[nd] == 1) col[nd] = 3;
}
}
inline void To(int u, int v, int c, int nd) {
Qy(c, u), Qy(c, v), Qy(c, nd);
}
bool Check(int i, int u, int v) { return e[i].u == u and e[i].v == v; }
void Tarjan(int u, int fro = 0) {
if (fro) stke[++*stke] = fro;
dfn[u] = low[u] = ++idx, stk[++*stk] = u; in[u] = true;
ep(i, u, v) {
if (!dfn[v]) {
Tarjan(v, i);
low[u] = std::min(low[u], low[v]);
if (low[v] >= dfn[u]) { int nw, p = *stk, cnt = 0;
++scc;
Ae(u, n + scc);
while (stk[p] != v) --p;
rep(i, *stk, p) Ae(stk[i], n + scc);
while (!Check(stke[*stke], u, v)) {
nw = stke[(*stke)--];
To(e[nw].u, e[nw].v, e[nw].w, n + scc);
}
nw = stke[(*stke)--];
To(e[nw].u, e[nw].v, e[nw].w, n + scc);
rep(i, *stk, p) {
if (col[stk[i]] == 3) ++cnt;
col[stk[i]] = 0;
in[stk[i]] = false;
}
if (col[u] == 3) ++cnt;
col[u] = 0;
if (cnt == 2) ++ans;
*stk = p - 1;
}
}
else {
if (in[v]) stke[++*stke] = i;
low[u] = std::min(low[u], dfn[v]);
}
}
}
ll C2(ll n) { return n * (n - 1) / 2; }
int Find(int x, int p) { return fa[p][x] == x ? x : fa[p][x] = Find(fa[p][x], p); }
void Merge(int u, int v, int p) {
if ((u = Find(u, p)) != (v = Find(v, p)))
fa[p][u] = v, tot[p][v] += tot[p][u];
}
int main() {
read(), n = read(), m = read(); int u, v, c;
lep(i, 1, m) {
u = read(), v = read(), c = getchar();
while (c != 'D' and c != 'd') c = getchar();
AddE(u, v, c == 'D'), AddE(v, u, c == 'D');
}
Tarjan(1);
lep(i, 1, n + scc) {
fa[0][i] = fa[1][i] = i;
if (i <= n) tot[0][i] = tot[1][i] = 1;
}
lep(i, n + 1, n + scc) {
if (col[i] == 1) for (int j : e1[i]) Merge(i, j, 0);
if (col[i] == 2) for (int j : e1[i]) Merge(i, j, 1);
}
lep(i, 1, n + scc) {
if (fa[0][i] == i) ans += C2(tot[0][i]);
if (fa[1][i] == i) ans += C2(tot[1][i]);
}
ans = C2(n) - ans;
printf("%lld\n", ans);
return 0;
}
[APIO2018] 铁人两项
给定一个无向图,计数三元组 \((u,v,f)\) 满足存在 \(u\) 到 \(v\) 和 \(v\) 到 \(f\) 的简单路径,且两条路径除点 \(v\) 不交。
路径为点集,简单路径即不经过重复点。
点击查看
当 \(u\) 和 \(f\) 确定时, \(v\) 的合法数量即 \(u\) 到 \(f\) 的所有路径的并的点数 \(- 2\) (减去 \(u\) 和 \(f\) 本身)。
而两个点之间所有简单路径的并也就是两点之间所有点双的并。
简单想一下的话:走出一个点双便不能再回来,而路过一个点双,其内部的所有点一定也可以经过,两个端点所在点双需要对端点是否为割点特判。
但如果我们对原图建一个圆方树,每经过一个方点就累加它所代表点双的大小呢?
可是这样割点就会算两次,于是我们把每个圆点都赋一个 \(-1\) 的值,每个方点都赋值为它所代表点双的大小。
惊讶的发现,这时两个圆点之间的路径和(圆方树上)便是所有 \(v\) 的可能方案数。
计算所有圆点之间的贡献是容易的。
\(Dfs\) 即可。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
typedef long long ll;
const int _ = 4e5 + 7;
int n, m, u, v, dfn[_], idx, low[_], scc;
int siz[_], bel[_], stk[_], val[_];
std::vector <int> e1[_], e2[_]; ll ans;
void D1(int u, int f, int rt) {
dfn[u] = low[u] = ++idx, bel[u] = rt, stk[++*stk] = u;
for (int v : e1[u]) {
if (!dfn[v]) {
D1(v, u, rt);
if (low[v] == dfn[u]) {
++scc, ++val[n + scc], bel[n + scc] = rt;
e2[n + scc].push_back(u), e2[u].push_back(n + scc);
while (stk[*stk] != v) { int nw = stk[(*stk)--];
e2[n + scc].push_back(nw), e2[nw].push_back(n + scc),
++val[n + scc];
}
int nw = stk[(*stk)--];
e2[n + scc].push_back(nw), e2[nw].push_back(n + scc),
++val[n + scc];
}
low[u] = std::min(low[u], low[v]);
}
else low[u] = std::min(low[u], dfn[v]);
}
}
void D2(int u, int f) {
if (u <= n) siz[u] = 1;
for (int v : e2[u]) if (v != f) D2(v, u), siz[u] += siz[v];
}
void D3(int u, int f) {
if (u <= n) {
ll res = 1;
for (int v : e2[u]) if (v != f) {
D3(v, u);
ans -= res * siz[v], res += siz[v];
}
ans -= 1ll * siz[u] * (siz[bel[u]] - siz[u]);
}
else {
ll res = 0;
for (int v : e2[u]) if (v != f) {
D3(v, u);
ans += 1ll * val[u] * siz[v] * res, res += siz[v];
}
ans += 1ll * val[u] * siz[u] * (siz[bel[u]] - siz[u]);
}
}
int main() {
scanf("%d%d", & n, & m);
lep(i, 1, m) scanf("%d%d", & u, & v),
e1[u].push_back(v), e1[v].push_back(u);
lep(i, 1, n) if (!dfn[i]) D1(i, 0, i);
lep(i, 1, n) if (bel[i] == i) D2(i, 0);
lep(i, 1, n) if (bel[i] == i) D3(i, 0);
printf("%lld\n", ans * 2);
return 0;
}
CF487E Tourists
你要处理 \(q\) 个操作:
C a w: 表示 \(a\) 城市的纪念品售价变成 \(w\)。
A a b: 表示有一个游客要从 \(a\) 城市到 \(b\) 城市,你要回答在所有他的旅行路径中最低售价的最低可能值。
点此查看
树剖,并 set 维护每个方点的儿子信息,查询时根据需要查询 \(LCA\) 父亲的值。
只维护儿子是一个经典树上维护信息的 trick 。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, d) for (int i = H[u], d = e[i].v; i; i = e[i].n, d = e[i].v)
const int _ = 1e6 + 7;
const int inf = 2e9;
struct Edge { int v, n; }e[_]; int cnte = 1, H[_];
int n, m, q, w[_];
int dfn[_], low[_], stk[_], idx, scc;
int son[_], siz[_], dep[_], fa[_], top[_], uid[_];
int mn[_], L[_], R[_];
std::multiset <int> S[_];
std::vector <int> e1[_];
#define ls p << 1
#define rs p << 1 | 1
void PushUp(int p) { mn[p] = std::min(mn[ls], mn[rs]); }
void Build(int l, int r, int p) {
L[p] = l, R[p] = r, mn[p] = inf;
if (l == r) { mn[p] = w[uid[l]]; return; } int mid = l + r >> 1;
Build(l, mid, ls), Build(mid + 1, r, rs); PushUp(p);
}
void Modify(int d, int k, int p) {
if (d < L[p] or R[p] < d) return;
if (L[p] == R[p]) { mn[p] = k; return; }
Modify(d, k, ls), Modify(d, k, rs); PushUp(p);
}
int Gets(int l, int r, int p) {
if (r < L[p] or R[p] < l) return inf;
if (l <= L[p] and R[p] <= r) return mn[p];
return std::min(Gets(l, r, ls), Gets(l, r, rs));
}
#undef ls
#undef rs
void Dfs1(int u, int f) {
dep[u] = dep[fa[u] = f] + 1, siz[u] = 1;
for (int v : e1[u]) if (v != f) {
if (u > n) S[u].insert(w[v]);
Dfs1(v, u); siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
if (u > n) w[u] = *S[u].begin();
}
void Dfs2(int u, int tp) {
dfn[u] = ++idx, top[u] = tp, uid[idx] = u;
if (!son[u]) return;
Dfs2(son[u], tp);
for (int v : e1[u]) if (v != fa[u] and v != son[u])
Dfs2(v, v);
}
int Query(int x, int y) {
int ans = inf;
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) std::swap(x, y);
ans = std::min(ans, Gets(dfn[top[x]], dfn[x], 1));
x = fa[top[x]];
}
if (dep[x] > dep[y]) std::swap(x, y);
ans = std::min(ans, Gets(dfn[x], dfn[y], 1));
if (x > n) ans = std::min(ans, w[fa[x]]);
return ans;
}
void Update(int x, int k) {
if (fa[x]) {
S[fa[x]].erase(S[fa[x]].find(w[x])),
S[fa[x]].insert(k);
Modify(dfn[fa[x]], w[fa[x]] = *S[fa[x]].begin(), 1);
}
Modify(dfn[x], w[x] = k, 1);
}
void AddE(int u, int v) { e[++cnte] = { v, H[u] }, H[u] = cnte; }
void Ae(int u, int v) { e1[u].push_back(v), e1[v].push_back(u); }
void Tarjan(int u) {
dfn[u] = low[u] = ++idx, stk[++*stk] = u;
ep(i, u, v) {
if (!dfn[v]) {
Tarjan(v);
low[u] = std::min(low[u], low[v]);
if (low[v] >= dfn[u]) {
++scc; int nw;
Ae(u, n + scc);
while (stk[*stk] != v) {
nw = stk[(*stk)--];
Ae(nw, n + scc);
}
nw = stk[(*stk)--];
Ae(nw, n + scc);
}
}
else low[u] = std::min(low[u], dfn[v]);
}
}
int main() {
scanf("%d%d%d", & n, & m, & q);
lep(i, 1, n) scanf("%d", w + i); int u, v;
lep(i, 1, m) scanf("%d%d", & u, & v),
AddE(u, v), AddE(v, u);
Tarjan(1); idx = 0;
Dfs1(1, 0), Dfs2(1, 1);
Build(1, n + scc, 1);
char c; int x, y;
while (q--) {
c = getchar();
while (c != 'C' and c != 'A') c = getchar();
scanf("%d%d", & x, & y);
if (c == 'C') Update(x, y);
else printf("%d\n", Query(x, y));
}
return 0;
}
[USACO23OPEN] Triples of Cows P
最初,农夫 John 的 \(N\) 头编号为 \(1 \dots N\) 的奶牛中有 \(N-1\) 对朋友关系,形成一棵树。奶牛们依次离开农场去度假。在第 \(i\) 天,第 \(i\) 头奶牛离开农场,然后所有仍在农场中的第 \(i\) 头奶牛的朋友之间会成为朋友。
对于每个 \(i\) 从 \(1\) 到 \(N\),在第 \(i\) 头奶牛离开之前,有多少个有序三元组 \((a, b, c)\) 满足以下条件:\(a, b, c\) 均未离开农场,\(a\) 与 \(b\) 是朋友,且 \(b\) 与 \(c\) 是朋友?
点此查看
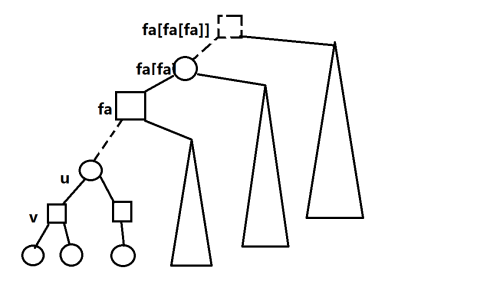
发现直接连边的复杂度爆炸,建立若干方点,与同一个方点相连的圆点表示其相互之间有边,而删点即把与它相连的方点合并。
发现维护方案数需要儿子个数,儿子的儿子个数和,儿子的儿子个数的平方和。
并查集维护信息即可。
#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define ep(i, u, d) for (int i = H[u], d = e[i].v; i;i = e[i].n, d = e[i].v)
typedef long long ll;
const int _ = 2e6 + 7;
struct edge { int v, n; } e[_]; int cnte = 1, H[_];
int n, fa[_], rt[_]; ll s[_], t[_], r[_], ans[_], res;
void AddE(int u, int v) { e[++cnte] = { v, H[u] }, H[u] = cnte; }
ll A3(ll n) { return n * (n - 1) * (n - 2); }
int Find(int x) { return rt[x] == x ? x : rt[x] = Find(rt[x]); }
void Init(int u, int f) {
fa[u] = f;
rt[u] = (u <= n) ? f : u;
ep(i, u, v) if (v != f) {
Init(v, u);
if (u <= n) s[u] += s[v], r[u] += s[v] * s[v];
else ++s[u], t[u] += s[v];
}
if (u <= n) ans[u] = s[u] * s[u] - r[u];
else ans[u] = 2 * s[u] * t[u] + A3(s[u] + 1);
res += ans[u];
}
void Merge(int u, int v) {
u = Find(u), v = Find(v);
if (u != v) rt[u] = v;
}
void Del(int u) {
int f = Find(u); ll tot = -1, dl = -s[u];
Merge(u, f);
ep(i, u, v) if (v != fa[u])
res -= ans[v], tot += s[v], dl += t[v], Merge(v, f);
res -= ans[u];
if (fa[f] != n) {
int ff = Find(fa[f]);
t[ff] += tot;
ans[ff] += 2 * s[ff] * tot;
res += 2 * s[ff] * tot;
}
res -= ans[fa[f]];
s[fa[f]] += tot, r[fa[f]] -= s[f] * s[f];
res -= ans[f];
s[f] += tot, t[f] += dl; r[fa[f]] += s[f] * s[f];
ans[fa[f]] = s[fa[f]] * s[fa[f]] - r[fa[f]];
res += ans[fa[f]];
ans[f] = 2 * s[f] * t[f] + A3(s[f] + 1);
res += ans[f];
}
int main() {
scanf("%d", & n); int u, v;
lep(i, 1, n - 1) {
scanf("%d%d", & u, & v);
AddE(u, n + i), AddE(n + i, u),
AddE(v, n + i), AddE(n + i, v);
}
Init(n, 0);
printf("%lld\n", res);
lep(i, 1, n - 1) {
Del(i);
printf("%lld\n", res);
}
return 0;
}
感谢 @Zelensky 指出本文的一些笔误。
时间仓促,如有错误欢迎指出,欢迎在评论区讨论,如对您有帮助还请点个推荐、关注支持一下

 如题
如题

 浙公网安备 33010602011771号
浙公网安备 33010602011771号