背包问题
[TOC]
##完全背包
有n种物品,第i种物品每个重量为wi,价值为vi,有无限多个。现有一个大小为m的背包,求能装下的最大总价值。
设$f(i)$表示用容量为i的背包能装下的最大价值,那么可以得到状态转移方程:
\(f(i)=\max\{f(i-w_1)+v_1,f(i-w_2)+v_2,......,f(i-w_n)+v_n\}\)
即
\(f(i)=\max\{f(i),f(i-w_j)+v_j\}\)
初始条件:\(f(0)=0\)
代码:
for(int i=1;i<=n;i++){ //物品种类从1~n
for(int j=w[i];j<=m;j++){ //正序循环
f[j]=max(f[j],f[j-w[i]]+v[i]);
//f[j-w[i]]可能已经装过第i种物品了(无限个)
}
}
//因为每种物品有无限个,所以交换两重循环顺序也是可以的
for(int i=0;i<=m;i++){
for(int j=1;j<=n;j++){
if(i>=w[j]) f[i]=max(f[i],f[i-w[j]+v[j]);
}
}
复杂度 O(nm)
模板题:洛谷p1616疯狂的采药
##01背包
有n种物品,第i种物品每个重量为wi,价值为vi,每种物品只有一个。现有一个大小为m的背包,求能装下的最大总价值。
如果仍然像完全背包一样设计状态,那么我们并不能知道哪些物品已经使用过,那些没有使用过,所以并不能进行正确的递推。
我们考虑子问题,对于一个物品,有取和不取两种可能,那么对这两种情况分别考虑,就可以得到两个规模更小的子问题:
1)不取第i个物品,问题转化为只有前i-1个物品,背包大小相同的子问题。
2)取第i个物品,问题转化为只有前i-1个物品,背包大小为当前背包大小减去第i个物品重量的子问题。
在两个里面取最大的即可。
###二维数组
于是我们设计状态$f(i,j)$表示容量为j的背包装前i个物品所能得到的最大价值。
那么$f(i,j)=\max{(f(i-1,j),f(i-1)(j-w_i)+v_i)}$
初始条件 \(f(i,0)=0,f(0,i)=0\)
代码:
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
if(j>=w[i]){
f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
}else{
f[i][j]=f[i-1][j];
}
}
}
时间复杂度和空间复杂度都为O(nm)。
###滚动数组
我们可以观察到在更新第i行的$f(i,)$时只用到了第i-1行的$f(i-1,)$,而再前面的数组则是浪费的。相当于有用的数组只有两行,于是我们可以想到用滚动数组来减少空间消耗。
代码:
int p=1,q=0;
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
if(j>=w[i]){
f[p][j]=max(f[q][j],f[q][j-w[i]]+v[i]);
}else{
f[p][j]=f[q][j];
}
//用前一行更新当前行
}
swap(p,q); //数组在两行之间滚动
}
###一维数组
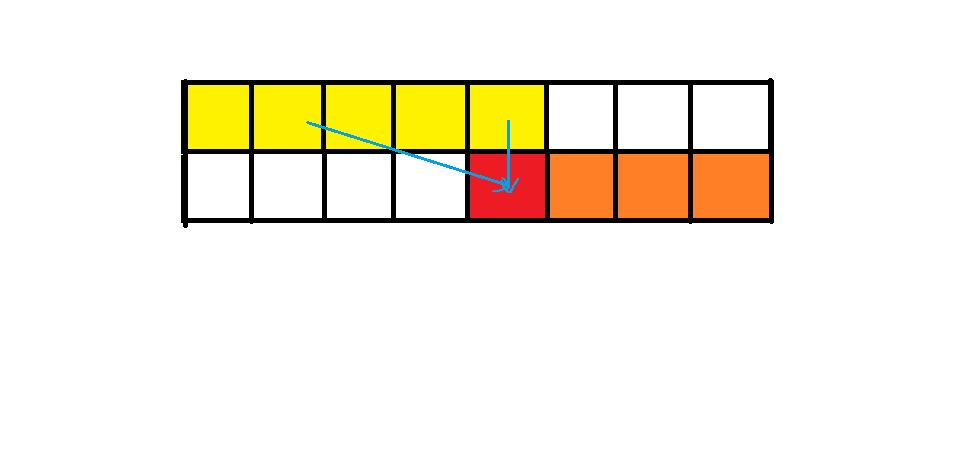
当然,我们还可以进行压缩,由上图看出,更新当前的只用到了他左上的部分,如果我们从后往前更新,那么整个有用的数组可以看作一行。也就是说我们可以用一维数组来实现01背包。
代码:
for(int i=1;i<=n;i++){
for(int j=m;j>=w[i];j--){
//倒序!!如果是正序那么一个物品就可能选择了多次,就是完全背包了
f[j]=max(f[j],f[j-w[i]]+v[i]);
//j在w[i]~0的时候不用更新是因为不能选择第i个物品,只能由前一行的当前位置更新得到,也就是f[i][j]=f[i][j-1],而在一维数组中,不需要操作就能更新得到。
}
}
这样,我们就将空间复杂度压到了O(m)。
模板题:洛谷p1048采药
通过01背包和完全背包这两个基础问题,我们可以解决更多的背包问题
##多重背包
有n种物品,第i种物品每个重量为wi,价值为vi,第i种物品有ci个。现有一个大小为m的背包,求能装下的最大总价值。
我们可以尝试将它转化成已知的问题。将有$c_i$个的第i种物品,看成$c_i$个物品,然后用01背包做。当然,这样的拆法数很多,是O(\(\sum c_i\)),时间复杂度是O(\(nm\sum c_i\))。
如果我们可以将$c_i$个b物品拆分成更少的数,且这些数的不同组合能表示出1~$c_i$中的所有数,那么我们就可以减少时间复杂度。
整数拆分
假设我们用k个数表示1n,那么我们最多可以表示出$2k$个数(k个数种每个数有选或不选两种可能,乘法原理),所以$2k\geq n$,也就是$k\geq log_2 n$,s这是k的下限。
一种可以构造出来的解是:
1.将1,2,4,......,$2i$不断加入集合,直至再加入下一个数时,和会超过n。
2.将$t=n-\sum 2i$加入集合
可以算出$\sum 2^i\geq n/2$,那么:
1.对于任意的$x\leq n/2$,x总能用1$2i$表示出来(二进制,选择了$2j$表示二进制中第j位为1。如$5_2=101$,那么我们就选择$20$和$22$)。
2.对于任意$x\geq n/2$,我们先选择t,那么$x-t\leq n/2$,我们再用第一种情况解决即可。
所以,这样的k个数是最少的可能。
代码:
int ans[N],cnt; //ans存放拆分成的整数
for(int i=1;i<=n;i*=2){
ans[++cnt]=i;
n-=i;
}
if(n>0){
ans[++cnt]=n;
}
由于每种物品最多有m/w[i]个,所以物品最多被拆成$O(logmin{\frac,c_i})$份,时间复杂度就是$O(nmlogm)$。
最后,我们再进行01背包即可。
模板题::洛谷p1776宝物筛选
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=2010,W=40010;
int n,m;
int v[N],w[N],f[W];
int cnt;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
int val,weight,c;
scanf("%d%d%d",&val,&weight,&c);
for(int i=1;i<=c;i*=2){ //整数拆分
v[++cnt]=i*val;
w[cnt]=i*weight;
//拆分后的每个物品价值,重量,3拆成1,2,那么价值就分别是1*v1,2*v1
c-=i;
}
if(c>0){
v[++cnt]=c*val;
w[cnt]=c*weight;
}
}
for(int i=1;i<=cnt;i++){ //01背包
for(int j=m;j>=w[i];j--){
f[j]=max(f[j],f[j-w[i]]+v[i]);
}
}
printf("%d\n",f[m]);
return 0;
}
##二维费用背包
在之前的问题上,每个物品都有两个维度的费用(如体积和重量,\(z_i,w_i\)),都不能超过背包容量。
那么状态转移方程为:
\(f(i,j,k)=\max\{f(i-1,j,k),f(i-1,j-w_i,j-z_i)+v_i\}\)
其中$f(i,j,k)$表示只有前i种物品,背包重量和体积不超过j,w所能装下的最大价值。
优化:类似于01背包,可以通过滚动数组,倒叙循环去掉第一维两种方法进行优化。
##混合背包
顾名思义,是01背包,完全背包,多重背包的混合。有的物品只能取一次,有的无限次,有的有限次。
显然,我们可以想到将他们当成多重背包来做(01背包就是物品只有1个,完全背包物品有$\frac$个)。复杂度O(nmlogm)。
第二种,把多重背包拆分,当成01背包,遇到01背包就逆序,遇到完全背包就正序循环。
模板题:洛谷p1833樱花
代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10,M=1e3+10;
int m,n;
int h1,h2,m1,m2;
int t[N],v[N],f[M],cnt,ans;
int main(){
scanf("%d:%d %d:%d %d",&h1,&m1,&h2,&m2,&n);
m=h2*60+m2-(h1*60+m1);
for(int i=1;i<=n;i++){
int t1,v1,c;
scanf("%d%d%d",&t1,&v1,&c);
if(c==0){ //c==0是完全背包,最多m/t1个
c=m/t1;
}
for(int j=1;j<=c;j*=2){ //拆分
v[++cnt]=j*v1;
t[cnt]=j*t1;
c-=j;
}
if(c>0){
v[++cnt]=c*v1;
t[cnt]=c*t1;
}
}
for(int i=1;i<=cnt;i++){
for(int j=m;j>=t[i];j--){
f[j]=max(f[j],f[j-t[i]]+v[i]);
}
}
for(int i=1;i<=m;i++){
ans=max(ans,f[i]);
}
printf("%d\n",ans);
return 0;
}
##分组背包
01背包的基础上,每个物品属于一个组,每组最多取一个物品。
把每个组当成一个物品,可以取其中的一个,或者不取。
设$f(i,j)$表示对于前i组,用容量为j的背包能装下的最大价值。
状态转移方程:\(f(i,j)=\max_k_\in_G_i\{f(i-1,j),f(i-1,j-w_k)+v_k\}\)
模板题:洛谷p1757通天之分组背包
代码:
#include<cstdio>
#include<iostream>
#include<vector>
using namespace std;
const int N=1e3+10,M=1e3+10;
int n,m;
vector<int> G[110];
int a[N],b[N],c[N],f[M];
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++){
scanf("%d%d%d",&a[i],&b[i],&c[i]);
G[c[i]].push_back(i); //每一组有哪些物品
}
for(int i=1;i<=100;i++){
for(int j=m;j>=0;j--){ //逆序,选一次
for(int k=0;k<G[i].size();k++){
int v=G[i][k];
if(j-a[v]>=0){
f[j]=max(f[j],f[j-a[v]]+b[v]);
}
}
}
}
printf("%d\n",f[m]);
return 0;
}
##树形背包
01背包的基础上,有些物品可能依赖于其他物品(A依赖于B表示选了B才能选A),并且依赖关系构成一棵树。有时一些物品没有依赖,那么会成为一片森林,我们可以增加重量和价值都为0的虚拟物品,将其作为这些物品的依赖,从而构成一棵树。
dfs序
对一棵树进行先序遍历,有如下性质:
- 对每一棵子树,树根在dfs序中最先出现
- 一棵子树在dfs序中对应连续的一段区间
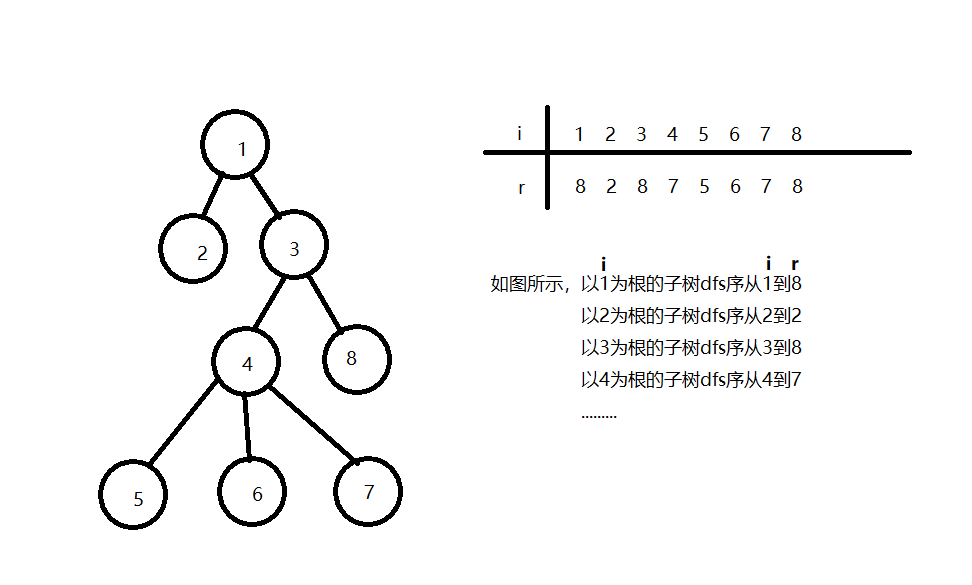
按照dfs序从后往前的顺序,对每个物品,有选和不选两种可能
1.选,转化成dfs序中它的下一个的子问题(eg:选4,转化成5的子问题)
2.不选,那么它的整棵子树也不能选,转化成dfs序中它子树的最右的下一个(eg:不选4,转化成8的子问题
设$f(i,j)$表示对于dfs序中i~n的物品,容量为j的背包,最多能装的价值。
设节点i在dfs序中子树的最后一个节点为$r_i$,则转移方程为:
\(f(i,j)=\max\{f(r_i+1,j),f(i+1,j-w_i)+v_i\}\)
时间复杂度O(nm)。
模板题:洛谷p2014选课
代码:
#include<cstdio>
#include<iostream>
#include<vector>
using namespace std;
const int N=300+10;
int n,m,cnt;
int v[N],id[N],di[N],ri[N],f[N][N];
vector<int> G[N];
void dfs(int x){
id[x]=cnt; //x的dfs序号
di[cnt]=x; //dfs序号为cnt的数
cnt++;
//遍历边
for(int i=0;i<G[x].size();i++){
int v=G[x][i];
dfs(v);
}
ri[id[x]]=cnt; //下一颗子树(存的是上面转移方程的ri+1)
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
int k;
scanf("%d%d",&k,&v[i]);
G[k].push_back(i); //以k为依赖的节点(建树)
}
dfs(0);
//深度优先遍历,得出dfs序(建立了一个虚拟节点)
for(int i=n;i>=0;i--){ //dfs序从后往前
for(int j=0;j<=n;j++){
if(j>=1){
f[i][j]=max(f[ri[i]][j],f[i+1][j-1]+v[di[i]]);
}else{
f[i][j]=f[ri[i]][j];
}
}
}
printf("%d\n",f[0][m+1]); //根节点重量是1
return 0;
}
##应用
1.洛谷p1164小A点菜
题意:m元,n种菜,每种ai元,只能点一份,求正好把钱花完的方案数。
类似于01背包,变成了计数问题。
设$f(i,j)$表示之有前i道菜,花费j元的方案,转移方程:
\(f(i,j)=f(i-1,j)+f(i-1,j-ai)\)
初始条件:\(f(i,0)=1,f(0,j)=0;(j>0)\)
代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int N=110,M=1e4+10;
int n,m;
int a[N],f[N][M];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",a+i);
}
for(int i=0;i<=n;i++) f[i][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(j>=a[i]) f[i][j]=f[i-1][j]+f[i-1][j-a[i]];
else f[i][j]=f[i-1][j];
}
}
printf("%d\n",f[n][m]);
return 0;
}
题意:将1~n的数分成两个集合,是他们的总和相等,问有几种本质不同的方案。
由题意得,每个集合的和应该为$\frac{n(n+1)}{4}$,如果不能整除,答案为0。
问题转化为从1~n个数中选出一些,使他们的和为$\frac{n(n+1)}{4}$。
因为要求本质不同,最后答案除以2.
设$f(i,j)$表示只选前i个数,总和为j的方案数,转移方程:
\(f(i,j)=f(i-1,j)+f(i-1,j-i)\)
初始条件:\(f(i,0)=1,f(0,j)=0;(j>0)\)
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=40,M=420;
typedef long long ll;
ll n,m,ans,f[N][M];
int main(){
scanf("%lld",&n);
if(n%4==0||(n+1)%4==0){
m=n*(n+1)/4;
for(int i=0;i<=n;i++) f[i][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(j>=i) f[i][j]=f[i-1][j]+f[i-1][j-i];
else f[i][j]=f[i-1][j];
}
}
ans=f[n][m]/2;
}else{
ans=0;
}
printf("%lld\n",ans);
return 0;
}
3.洛谷p1064金明的预算方案
树形背包
代码:
#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
const int N=65,M=35010;
int n,m,cnt;
int v[N],p[N],ri[N],id[N],di[N];
vector<int> G[N];
int f[N][M];
void dfs(int x){
id[x]=cnt;
di[cnt]=x;
cnt++;
for(int i=0;i<G[x].size();i++){
int v=G[x][i];
dfs(v);
}
ri[id[x]]=cnt;
}
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++){
int q;
scanf("%d%d%d",&v[i],&p[i],&q);
G[q].push_back(i);
}
dfs(0);
for(int i=n;i>=0;i--){
for(int j=0;j<=m;j++){
int ii=di[i];
if(j>=v[ii]) f[i][j]=max(f[ri[i]][j],f[i+1][j-v[ii]]+v[ii]*p[ii]);
else f[i][j]=f[ri[i]][j];
}
}
printf("%d\n",f[0][m]);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号