《算法导论》——深度优先搜索与拓扑排序
深度遍历算法描述
算法描述参考自《算法导论》深度优先搜索算法:
/*
注解:
1、G.v表示途中节点的集合,其中G是一个有向图
2、G:Adj[u] 表示再有向图中以u为起始节点的邻接节点集合
3、color 白色表示节点未被发现;灰色表示节点已经被发现但没有深搜完毕;黑色节点表示节点深搜完毕
4、u.d 表示节点访问的开始时间。u.f表示节点访问的结束时间。u.parent表示u的父节点,NIL表示父节点为空。
*/
DFS(G)
for each vertex u belong to G.V
u.color=WHITE
u.parent=NIL
time=0
for each vertex u belong to G.V
if u.color=WHITE
DFS-VISIT(G,u)
DFS-VISIT(G,u)
time=time+1
u.d=time
u.color=GRAY
for each v belong to G:Adj[u]
if v.color==WHITE
v.parent=u
DFS-VISIT(G,v)
u.coloe=BALCK
time=time+1
u.f=time
什么是拓扑排序
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。——百度百科
注意:若有向图中存在回路,则该有向图无法进行拓扑排序
常用的拓扑排序方法如下:
方法一:入度统计
(1)从有向图中选择一个没有前驱(即入度为0)的顶点并且输出它。
(2)从图中删去该顶点,并且删去从该顶点发出的所有边。
(3)重复上述步骤(1)和(2),直到当前有向图中不存在没有前驱结点的顶点为止,或者当前有向图中的所有结点均已输出为止。
(4)如果当前有向图中不存在没有前驱结点的顶点,并且当前有向图中的所有结点尚未完全输出,则可以判断当前有向图中有环
方法二:深度优先搜索
思路是记录各个节点深度遍历时完成访问的结束时间,然后根据结束时间的先后顺序组成一个列表,则该列表就是一个拓扑序列
拓扑排序DFS算法描述
算法描述参考自《算法导论》拓扑排序:
TOPOLOGICAL-SORT(G)
call DFS(G) to compute finishing times v.f for each vertex v
as each vertex is finished,insert it onto the front of a linked list
return the linked list of vertices
需要注意的是,基于深度优先搜索来实现拓扑排序,所用到的图必须是有向无环图
DFS代码实现
package myDFS;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class DFS {
private int nodeNum;//图的节点个数
private int[][] graph;//邻接矩阵存储图信息
private List<Edge> edges = new ArrayList<>();//存储边信息
private List<Integer> res = new ArrayList<>();//存放深度遍历的路径
private List<Integer> topoSort = new ArrayList<>();//存放拓扑排序路径
public static void main(String[] args) {
DFS dfs = new DFS();
dfs.inputInfo(); //输入图的信息
dfs.creatGraph(); //创建有向图
dfs.outputGraph(); //打印有向图
dfs.dfs(); //进行深度遍历
dfs.outputRes(); //输出结果
}
/**
* 用户输入,并创建边集合
*/
public void inputInfo() {
Scanner scanner = new Scanner(System.in);
System.out.print("请输入节点个数:");
nodeNum = scanner.nextInt();
int size = nodeNum;
System.out.println("请依次输入边,格式为:起始节点 终止节点(-1 -1作为结束符)");
while (true) {
int node1 = scanner.nextInt();
int node2 = scanner.nextInt();
if (node1 < 0 || node2 < 0)
break;
edges.add(new Edge(node1, node2));
}
}
/**
* 创建有图
*/
public void creatGraph() {
graph = new int[nodeNum + 1][nodeNum + 1];//因为节点从1开始编号,所以加一
for (int i = 0; i < edges.size(); i++) {
graph[edges.get(i).node1][edges.get(i).node2] = 1;
}
}
/**
* 深度遍历递归调用
*/
static int time = 0;
public void dfs() {
// visited访问标志符数组,有三种状态:
// visited=0表示节点未被发现
// visited=1表示节点已经被发现,但没有完成深搜
// visited=2表示节点已经深搜完毕
int visited[] = new int[nodeNum + 1];
int startTime[] = new int[nodeNum + 1];//用于记录各节点被发现的时间
int endTime[] = new int[nodeNum + 1];//用于记录各节点完成深搜的时间
time = 0;//全局时钟
//选择开始节点进行深搜
for (int i = 1; i <= nodeNum; i++) {
if (visited[i] == 0) {
dfs(graph, i, visited, startTime, endTime);
}
}
System.out.println("startT:" + Arrays.toString(startTime));
System.out.println("endT:" + Arrays.toString(endTime));
}
/**
* 递归实现深度遍历
*
* @param graph 有向图
* @param node 当前节点
* @param visited 访问标识符数组
* @param startT 开始时间数组
* @param endT 结束时间数组
*/
public void dfs(int graph[][], int node, int visited[], int startT[], int endT[]) {
res.add(node);//记录访问路径
time++; //节点被发现,更新时钟
visited[node] = 1;
startT[node] = time;
while (findNext(graph, node, visited) != -1) {
int nestNode = findNext(graph, node, visited);
if (visited[nestNode] == 0) {
dfs(graph, nestNode, visited, startT, endT);
}
}
time++;//节点深搜结束,更新时钟
endT[node] = time;
visited[node] = 2;
topoSort.add(node);
}
/**
* 获取当前节点的下一个节点
*
* @param graph 有向图
* @param node 当前节点
* @param visited 访问标志符数组
* @return -1表示没有下一个节点
*/
private int findNext(int[][] graph, int node, int visited[]) {
for (int i = 0; i < edges.size(); i++) {
Edge edge = edges.get(i);
if (edge.node1 == node && visited[edge.node2] == 0) {
return edge.node2;
}
}
return -1;
}
/**
* 打印有向图
*/
public void outputGraph() {
for (int i = 1; i <= nodeNum; i++) {
for (int j = 1; j <= nodeNum; j++) {
System.out.print(graph[i][j] + " ");
}
System.out.println();
}
}
/**
* 输出深度遍历的路径以及拓扑排序路径
*/
public void outputRes() {
System.out.println("访问路径" + res);
System.out.println("拓扑路径" + topoSort);
}
}
class Edge {
int node1;
int node2;
int weight;
public Edge(int node1, int node2) {
this.node1 = node1;
this.node2 = node2;
}
}
测试用例:
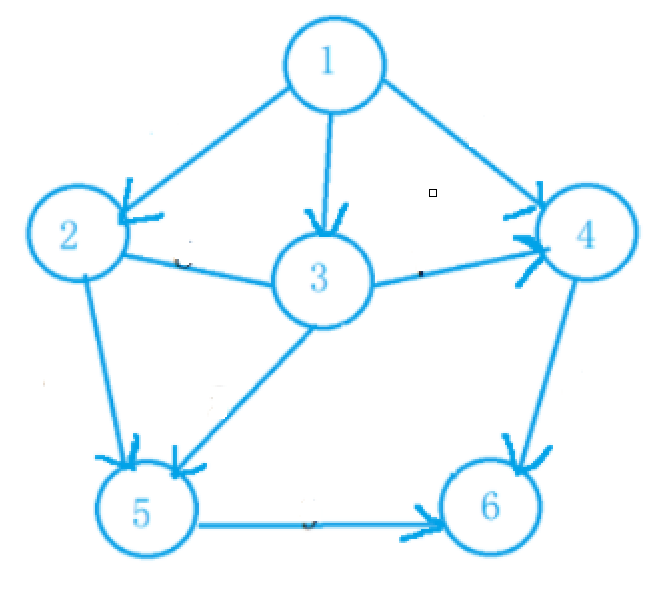
6
1 2
1 3
1 4
2 3
2 5
3 4
3 5
4 6
5 6
-1 -1
输出:
0 1 1 1 0 0
0 0 1 0 1 0
0 0 0 1 1 0
0 0 0 0 0 1
0 0 0 0 0 1
0 0 0 0 0 0
startT:[0, 1, 2, 3, 4, 8, 5]
endT:[0, 12, 11, 10, 7, 9, 6]
访问路径[1, 2, 3, 4, 6, 5]
拓扑路径[6, 4, 5, 3, 2, 1]
参考资料
- 《算法导论》深度优先搜索
- 什么是拓扑排序
- 拓扑排序及其Java实现


 浙公网安备 33010602011771号
浙公网安备 33010602011771号