树结构及存储

树结构是一种由节点和边构成数据结构

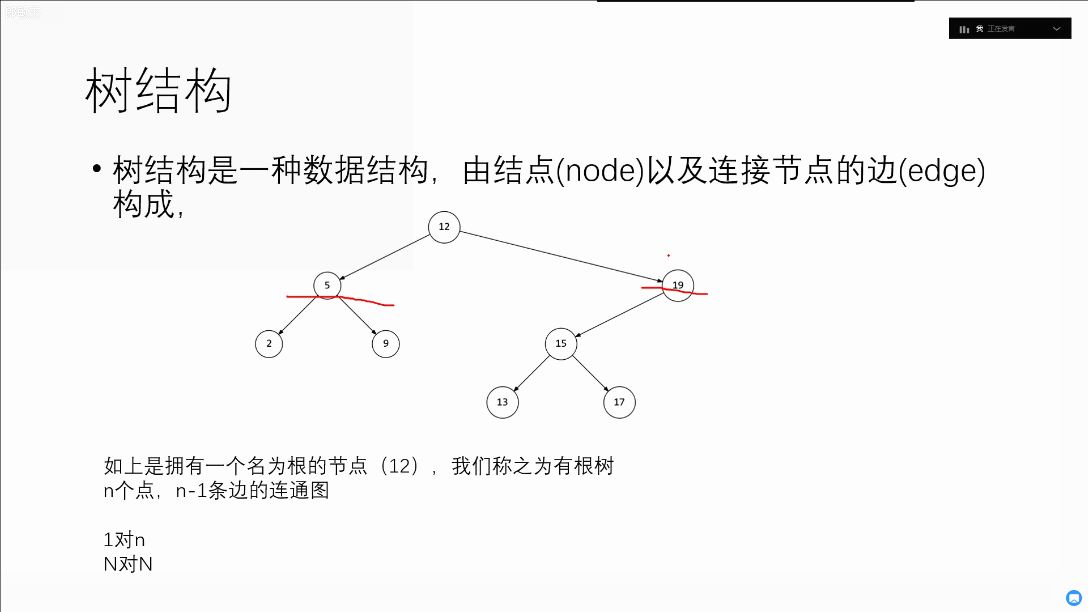
存储方法：左子右兄弟法

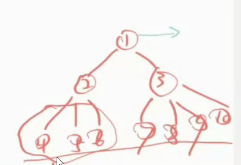
把上图的形式转化成下图的形式

例题链接：
https://vjudge.net/contest/486762#problem/A
题目思路：

例题代码：

#include <iostream>
using namespace std;
#define MAX 100005
#define NIL -1
 
struct Node {
    int parent;
    int left;
    int right;
};
 
Node T[MAX];
int n, D[MAX];
 
void print(int u)
{
    int i, c;
    cout << "node " << u << ": ";
    cout << "parent = " << T[u].parent << ", ";
    cout << "depth = " << D[u] << ", ";
     
    if(T[u].parent == NIL)
    {
        cout << "root, ";
    }
    else if(T[u].left == NIL)
    {
        cout << "leaf, ";
    }
    else
    {
        cout << "internal node, ";
    }
     
    cout << "[";
     
    for(i = 0, c = T[u].left; c != NIL; ++ i, c = T[c].right)
    {
        if(i)   cout << ", ";
        cout << c;
    }
     
    cout << "]" << endl;
}
 
// 递归求深度
void rec(int u, int p)
{
    D[u] = p;
    if(T[u].right != NIL)
    {
        rec(T[u].right, p);
    }
    if(T[u].left != NIL)
    {
        rec(T[u].left, p + 1);
    }
}
 
int main()
{
    int i, j, d, v, c, l, r;
    cin >> n;
    for(i = 0; i < n; ++ i)
    {
        T[i].parent = T[i].left = T[i].right = NIL;
    }
     
    for(i = 0; i < n; ++ i)
    {
        cin >> v >> d;
        for(j = 0; j < d; ++ j)
        {
            cin >> c;
            if(j == 0) 
            {
                T[v].left = c;  // 父节点的左孩子为c
            }
            else   
            {
                T[l].right = c; // 当前兄弟节点为c
            }
            l = c;  // 记录前一个兄弟节点
            T[c].parent = v;
        }
    }
    for(i = 0; i < n; ++ i)
    {
        if(T[i].parent == NIL)
        {
            r = i;
        }
    }
     
    rec(r, 0);
     
    for(i = 0; i < n; ++ i)
    {
        print(i);
    }
     
    return 0;
}

二叉树

二叉树是一种每个结点至多有两棵子树(即每个结点的度最大为2的有序树

满二叉树和完全二叉树

满二叉树的特点在于“满”，即每层的结点数都是最大结点数。
完全二叉树中的所有结点的编号必须和满二叉树的相同编号的结点在位置上完全相同。
换句话说，完全二叉树的结点按「自上向下，自左向右」的顺序不能中断。

二叉树的存储方法

与树同理
使用左子右兄弟的方法
但可以确定每个非叶子节点的子节点的数量为2(或1)
所以我们可以把每个非叶子节点的子节点分别定义为left和right
例题链接：
https://vjudge.net/contest/486762#problem/B

例题代码：

#include <iostream>

#define MAX 10007
#define NIL -1

using namespace std;

struct Node {
    int parent, left, right;
};

Node T[MAX];
int n, D[MAX], H[MAX];

void set_depth(int u, int d) {
    if (u == NIL) return;
    D[u] = d;
    set_depth(T[u].left, d + 1);
    set_depth(T[u].right, d + 1);
}

int set_height(int u) {
    int h1 = 0, h2 = 0;
    if (T[u].left != NIL)
        h1 = set_height(T[u].left) + 1;
    if (T[u].right != NIL)
        h2 = set_height(T[u].right) + 1;
    return H[u] = max(h1, h2);
}

int get_sibling(int u) {
    if (T[u].parent == NIL) return NIL;
    if (T[T[u].parent].left != u && T[T[u].parent].left != NIL)
        return T[T[u].parent].left;
    if (T[T[u].parent].right != u && T[T[u].parent].right != NIL)
        return T[T[u].parent].right;
    return NIL;
}

void print(int u) {
    cout << "node " << u << ": ";
    cout << "parent = " << T[u].parent << ", ";
    cout << "sibling = " << get_sibling(u) << ", ";

    int deg = 0;
    if (T[u].left != NIL) deg++;
    if (T[u].right != NIL) deg++;
    cout << "degree = " << deg << ", ";

    cout << "depth = " << D[u] << ", ";
    cout << "height = " << H[u] << ", ";

    if (T[u].parent == NIL)
        cout << "root" << endl;
    else if (T[u].left == NIL && T[u].right == NIL)
        cout << "leaf" << endl;
    else
        cout << "internal node" << endl;

}

int main() {
    int v, l, r, root = 0;
    cin >> n;

    for (int i = 0; i < n; i++) {
        T[i].parent = NIL;
    }

    for (int i = 0; i < n; i++) {
        cin >> v >> l >> r;
        T[v].left = l;
        T[v].right = r;
        if (l != NIL) T[l].parent = v;
        if (r != NIL) T[r].parent = v;
    }

    for (int i = 0; i < n; i++)
        if (T[i].parent == NIL)
            root = i;

    set_depth(root, 0);
    set_height(root);

    for (int i = 0; i < n; i++)
        print(i);

    return 0;
}