遗传算法详解与实验
遗传算法(Genetic Algorithm, GA)是一种通用的优化算法,属于进化算法簇中一个比较实用又有名的算法。进化算法融合了自然生物进化中共有的一些行为:繁殖、变异、竞争、选择等。
基本流程
GA通过迭代来优化目标函数的参数,直到目标函数满足一定条件时结束。迭代对目标函数的连续性并无要求,也就是说算法的迭代并不基于目标函数在当前参数下的梯度等连续性质。算法的转化思想是将所有待优化参数看做生物染色体,单个参数看做染色体上对应位置的基因,而目标函数看做生物对生存环境的适应度。大致的迭代流程如下:
0、随机生成一定数量的生物个体,它们的染色体各不相同,因此在生存环境中的适应度也不同。也就是说,这些随机生成的参数对目标函数的满足度各不相同。
1、根据个体对环境的适应度,适者生存。选择适应度较高的一部分个体,生存下来,有资格繁殖下一代,剩下的都死在这一代。当然这里也可以随机少量选择一些“幸运”的适应度较低的个体,让它们也能参与繁殖,增加多样性。
2、对选出的个体进行两两“交配”,交配就是让它们DNA中对应位置的基因进行交叉和变异产生新的个体(不知道交叉和变异的回去读高中生物书),得到下一代。具体的交配和交叉变异策略下面再详细介绍。
3、在新的一代,对所有个体进行判断,是否已经有个体满足目标函数的终极条件。有就结束迭代,否则回到1。
算法基本概念
串:表示生物个体的染色体,通常是二进制串,或根据优化需要使用其它形式的串。
群体和群体大小:个体的集合称为群体,串是群体的元素。群体中个体的数量称为群体大小。
基因:基因是串中的元素,用来表示个体特征。通常一个基因对应一个参数,或者在二进制编码时,一位就代表一个基因。
基因位置:基因在串中的位置,简称基因位。
串结构空间:基因任意组合所形成的串集合,也就是在当前优化背景下所有可能的串的集合。
适应度:表示某一个体对环境的适应程度,用一个函数表示,通常就是待优化的目标函数。
算法组成部分
介绍完GA的大致流程和基本概念,你应该对其有了个大致了解。下面开始详细讲解算法的各个组成部分,由四个部分组成:编码机制、适应度函数、控制参数、遗传算子。
编码机制
待优化的参数可以编码为各种形式的串,以便进行上述的遗传迭代。编码要是可逆的,也就是说串与参数之间应该是一一对应的,从而每次迭代都能解码并计算个体的适应度。并且GA的编码可以有个十分广泛的理解,不局限于简介中对待优化参数的编码。比如,在分类问题,串可解释为一个规则,即串的前半部为输入或前件,后半部为输出或后件、结论。因此,遗传算法可以对大量的问题进行建模,只要把问题的条件啊,约束啊,参数啊全都一股脑地编码丢进去“进化”就好了,这也是为什么它在数学建模比赛中如此热门的原因。
编码方式有二进制编码、格雷编码、实数编码等。二进制编码就是把参数都转换为二进制,然后排成一排,编码的每一位都看做一个基因。实数编码实际上就是不编码,当参数都为实数而且很多时,就可以直接把这些实数参数作为染色体基因。下面介绍格雷码。
格雷编码
格雷编码是对二进制编码进行变换后所得到的一种编码方法,它要求两个连续整数的编码之间只能有一个码位不同,其余码位都是完全相同的。因此,格雷码解决了二进制编码的汉明悬崖问题。二进制编码与格雷码之间的转换如下:
设有二进制串$b_1,b_2,...,b_n$,对应的格雷串为$a_1,a_2,…,a_n$,则从二进制编码到格雷编码的变换为:
$ a_i = \left\{ \begin{aligned} &b_i,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i=1\\ &b_{i-1}\oplus b_i,\;\;\;\;i>1 \end{aligned} \right. $
其中$\oplus$为异或运算。格雷码到二进制编码的变换为:
$b_i = (\sum\limits_{j=1}^ia_i)mod\; 2$
尽管转换式子有了,但是这样看不出格雷码的特点,下面通过列举格雷码来总结它的特点。
| 整数 | 格雷码 | |||||||
| 0 | 0 | |||||||
| 1 | 1 | |||||||
| 2-3 | 11 | 10 | ||||||
| 4-7 | 110 | 111 | 101 | 100 | ||||
| 8-15 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
可以发现,格雷码每增加一位,低位(仅除了最高位外)编码即为所有位数少于它的格雷码的反序排列。比如上面的四位格雷码,低三位分别是100、101、111、110、010、011、001、000,观察小于四位的格雷码,从7到0,格雷码同样也是100、101、111、110、010、011、001、000。
适应度函数
适应度函数用于判断个体对环境的适应度、评估个体,定出优劣程度。
原始适应度函数直接将待求解问题的目标函数$f(x)$定义为算法的适应度函数。比如求解极值问题
$\max\limits_{x\in [a,b]}f(x)$
直接将$f(x)$作为原始适应度函数。
还有其他的定义方式,但是因为对于不同问题,定义方式各不相同,所以不再举例,只要适应度函数是向着优化目标定义的即可(物种适应度越大,越接近你的优化目标)。
控制参数
在GA的实际操作时,需适当确定某些参数的值以提高选优的效果。这些参数包含:
字符串所含字符的个数,即串长。这一长度为常数,记为$L$。
每一代群体的大小,也称群体的容量,记为$n$。
交换率,即施行交换算子的概率,记为$P_c$。
突变率,即施行突变算子的概率,记为$P_m$。
遗传算子
遗传算子就是执行选择、交叉、变异等操作的方法。GA中最常用的算子有三种:选择算子、交叉算子、变异算子。
选择算子
选择算子从群体中按某一概率成对选择个体,某个体$x_i$被选择的概率$P_i$与其适应度值成正比。最通常的实现方法是轮盘赌型。
所谓轮盘赌,就是根据适应度函数来确定个体被选择的概率。如果适应度函数$f(x)>0$,则可以这样定义:
$\displaystyle P(x_i) = \frac{f(x_i)}{\sum\limits_{j=1}^Nf(x_j)}$
否则定义成softmax也行(我觉得):
$\displaystyle P(x_i) = \frac{\exp f(x_i)}{\sum\limits_{j=1}^N\exp f(x_j)}$
然后根据概率选择个体。这就是最简单的概率选择,不知道为什么要扯出一个所谓轮盘赌来,是怕别人理解不了吗。
交叉算子
交叉算子将被选中的两个个体的基因链按概率$P_c$进行交叉,生成两个新的个体。其中$P_c$是一个系统参数,通常看群体的大小,群体越小,$P_c$可以取得更大一些,但一般小于0.5。这是因为大于0.5等于把大部分基因都交换了,而这和交换剩余的小部分基因等价。具体来说,交叉有所谓的单点交叉、两点交叉、多点交叉、均匀交叉等。这些分类感觉没有任何意义,直接就按$P_c$进行交叉就行了。过程如下:
首先生成长度为$L$的二进制模板串,其中每位为1的概率为$P_c$。然后按照这个串对选择出来的两个父串进行交叉,为1的位置交叉,为0不交叉。比如对于两个父串
$X = 1011010$
$Y = 1101001$
模板串为
$T = 0101010$
则交叉后变为
$X'=1111000$
$Y'=1001011$
变异算子
变异算子将新个体的基因链的各位按概率$P_m$进行变异,$P_m$通常取得很小比如0.0001。对二值基因链(0,1编码)来说即是取反,对于实数基因来说,则可以在这个数的范围内取随机值,或是在某个固定范围内取随机值。另外,还可以进行基因之间的数字的调换、循环移动等。
总结
以上这些操作对于具体的优化任务而言,并没有什么原理可以讲解,也没有理论依据表明交叉和变异的确可以让个体更优。但是从宏观上来看,群体的适应度的确会在选择操作下不断向好发展,最终达到一个良好的点。归根结底,我认为这个算法就是在保持当前较好结果的前提下的随机迭代。它是十分随机的,有时可能迭代几步就搞定了,而有时可能几千步都出不来,所以会浪费大量的计算资源。而且对于很复杂的非凸问题,它同样也可能会陷入局部最优。所以能用传统方法求解的问题,尽量不用这种启发式算法。
实验
实验使用遗传算法求解以下函数的最大值:
$f(x,y) = 2\exp\left[\frac{-(x+3)^2-(y-3)^2}{10}\right] + 1.2\exp\left[\frac{-(x-3)^2-(y+3)^2}{10}\right] + \frac{1}{5}\exp\left[-\cos(3x)-\sin(3y)\right]$
$x,y$的范围都是$(-100,100)$,函数三维图像如下:

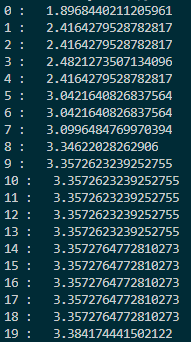
看表达式和图像可以判断最大值在$(-3,3)$附近。下面先以均匀分布产生1000个点,然后进行40次迭代。1000个点的迭代过程如下:
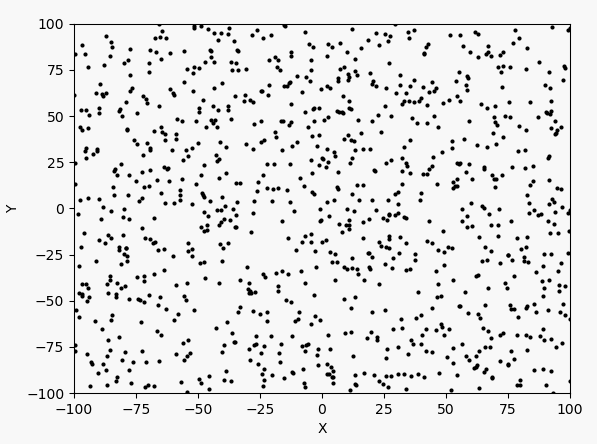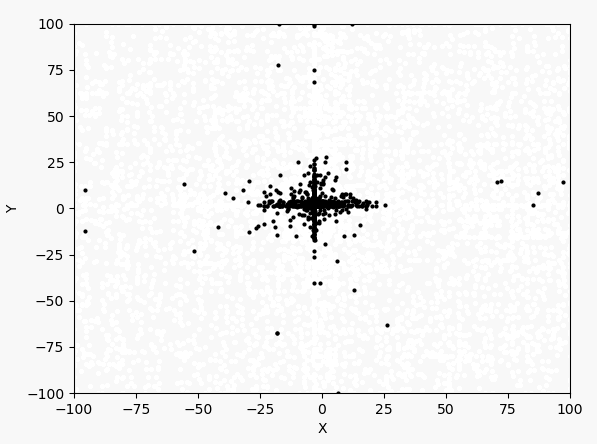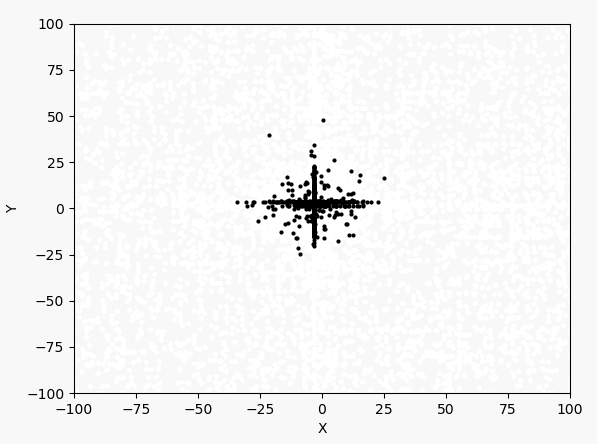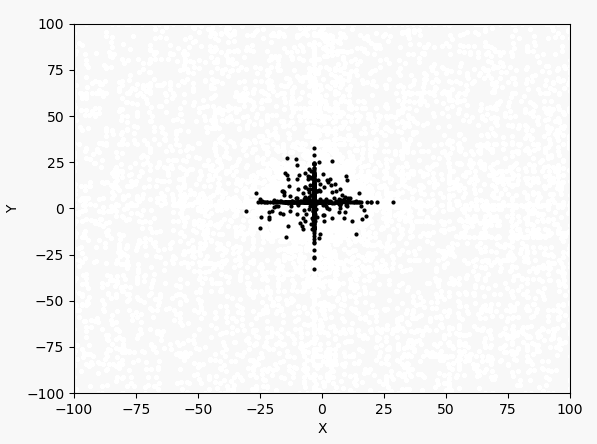
每次迭代的最大值和坐标:
 |
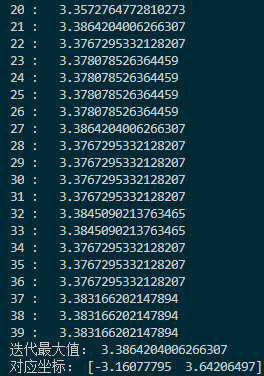 |
这里交叉率是0.2,变异率是0.3,变异使用的正态分布标准差是10,因此比较容易跳出这个函数的局部最优点。比如函数在$(3,-3)$附近的局部最优点,这点和$(-3,3)$之间差了$6\sqrt{2}$左右,刚好是10左右。另外,在$100\times 100$的范围内,把种群的大小设置为1000实际上过于饱和了,随随便便就找到了最优解,这和直接网格暴力搜索都有的一拼了。现在把种群大小调为200,变异标准差调为20,交叉率调为0.4,变异率调为0.1,看看迭代几次可以达到最优。以下是迭代过程图:

迭代了150次,也到了$(-3,3)$附近,时间上消耗少了一些。如果要再精确可能还要更多次的迭代,但因为它的变异方差较大,所以比较难。
以下是实验代码:
#%%定义函数 import time import numpy as np def func(X,Y): return np.exp((-(X+3)**2-(Y-3)**2)/10)*2 + np.exp((-(X-3)**2-(Y+3)**2)/10)*1.2 + np.exp(-np.cos(X*3)-np.sin(Y*3))/5 #%%遗传算法 time_start=time.time() dim = 2 iterate_times = 150 individual_n = 200 p_c = 0.4 p_m = 0.15 std_var = 20 num_range = [-100,100] def initialize(individual_n,num_range): return np.random.uniform(num_range[0],num_range[1],size = [individual_n,dim]) def overlapping(a,b,pc,dim): T = np.random.choice(a=2, size=dim,p=[1-pc,pc]) for i in range(dim): if T[i] == 1: a[i],b[i] = b[i],a[i] def variation(a,pm,dim,num_range): T = np.random.choice(a=2, size=dim,p=[1-pm,pm]) for i in range(dim): if T[i] == 1: a[i] = np.clip(np.random.normal(loc = a[i], scale=std_var),num_range[0],num_range[1]) def get_select_p(v): exp_v = np.exp(v) sum_exp_v = np.sum(exp_v) return exp_v/sum_exp_v def select_and_reproduction(population,num_range): values = func(population[:,0],population[:,1]) select_p = get_select_p(values) choices = np.random.choice(a=len(population), size=len(population), replace=True, p=select_p) new_population = population[choices] for i in range(int(len(new_population)/2)): overlapping(new_population[2*i],new_population[2*i+1],p_c,dim) variation(new_population[2*i],p_m,dim,num_range) variation(new_population[2*i+1],p_m,dim,num_range) argmax_value = np.argmax(values) return values[argmax_value],population[argmax_value],new_population population = initialize(individual_n,num_range) times_population = np.empty([iterate_times,individual_n,dim]) max_value = 0 max_value_coordinate = [] for i in range(iterate_times): times_population[i] = population last_max_value,last_max_value_pos,population = select_and_reproduction(population,num_range) if last_max_value>max_value: max_value = last_max_value max_value_coordinate = last_max_value_pos print(i,": ",last_max_value) time_end=time.time() print('总共耗时:',time_end-time_start) print('迭代最大值:',max_value) print('对应坐标:',max_value_coordinate) #%%画出种群的迭代过程 import matplotlib.pyplot as plt import matplotlib.animation as animation fig, ax = plt.subplots() xdata, ydata = [], [] ln, = plt.plot([], [],'ro',animated=True,color='black',markersize = 2) def init(): ax.set_xlim(num_range[0],num_range[1]) ax.set_ylim(num_range[0],num_range[1]) ax.set_xlabel('X') ax.set_ylabel('Y') return ln, def update(frame): frame = int(frame) xdata = times_population[frame,:,0] ydata = times_population[frame,:,1] ln.set_data(xdata, ydata) return ln, anim = animation.FuncAnimation(fig, update, frames=np.linspace(0,iterate_times-1,iterate_times),interval=100, init_func=init,blit=True) plt.show()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号