logistic回归和softmax回归
logistic:二分类
softmax:多分类
logistic回归
在 logistic 回归中,我们的训练集由 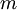 个已标记的样本构成:
个已标记的样本构成: 。由于 logistic 回归是针对二分类问题的,因此类标记
。由于 logistic 回归是针对二分类问题的,因此类标记 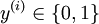 。
。
假设函数(hypothesis function): 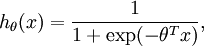
代价函数(损失函数):![\begin{align}J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^m y^{(i)} \log h_\theta(x^{(i)}) + (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) \right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/f/a/6/fa6565f1e7b91831e306ec404ccc1156.png)
 ,使其能够最小化代价函数。
,使其能够最小化代价函数。
假设函数就相当于我们在线性回归中要拟合的直线函数。
softmax回归
在 softmax回归中,我们的训练集由 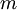 个已标记的样本构成:
个已标记的样本构成: 。由于softmax回归是针对多分类问题(相对于 logistic 回归针对二分类问题),因此类标记
。由于softmax回归是针对多分类问题(相对于 logistic 回归针对二分类问题),因此类标记  可以取
可以取  个不同的值(而不是 2 个)。我们有
个不同的值(而不是 2 个)。我们有 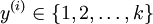 。
。
对于给定的测试输入  ,我们想用假设函数针对每一个类别j估算出概率值
,我们想用假设函数针对每一个类别j估算出概率值 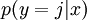 。也就是说,我们想估计
。也就是说,我们想估计  的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个
的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个  维的向量(向量元素的和为1)来表示这
维的向量(向量元素的和为1)来表示这  个估计的概率值。 具体地说,我们的假设函数
个估计的概率值。 具体地说,我们的假设函数 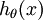 形式如下:
形式如下:
- 假设函数:
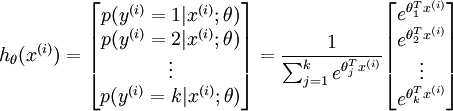
- 其中
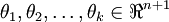 是模型的参数。请注意
是模型的参数。请注意 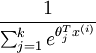 这一项对概率分布进行归一化,使得所有概率之和为 1 。
这一项对概率分布进行归一化,使得所有概率之和为 1 。 -
为了方便起见,我们同样使用符号
 来表示全部的模型参数。在实现Softmax回归时,将
来表示全部的模型参数。在实现Softmax回归时,将  用一个
用一个 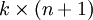 的矩阵来表示会很方便,该矩阵是将
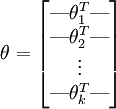
的矩阵来表示会很方便,该矩阵是将 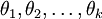 按行罗列起来得到的,如下所示:
按行罗列起来得到的,如下所示:
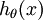 表示的是x属于不同类别的概率组成的向量。
表示的是x属于不同类别的概率组成的向量。- 代价函数:
![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/7/6/3/7634eb3b08dc003aa4591a95824d4fbd.png)
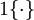 是示性函数,其取值规则为
是示性函数,其取值规则为
值为真的表达式
值得注意的是,logistic回归代价函数是softmax代价函数的特殊情况。因此,logistic回归代价函数可以改为:
![\begin{align}J(\theta) &= -\frac{1}{m} \left[ \sum_{i=1}^m (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) + y^{(i)} \log h_\theta(x^{(i)}) \right] \\&= - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=0}^{1} 1\left\{y^{(i)} = j\right\} \log p(y^{(i)} = j | x^{(i)} ; \theta) \right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/5/4/9/5491271f19161f8ea6a6b2a82c83fc3a.png)
- 一点个人理解:
-
为什么二分类中参数只有一个
 ,而k分类中参数却有k个。
,而k分类中参数却有k个。 -
其实二分类中的
 是y=1情况下的参数,而y=0情况下其实未给出参数,因为y=0的假设函数值可以通过1-(y=1的假设函数值)得到。同理,k分类中参数其实只需要k-1个参数就可以了,多余的一个参数是冗余的。
是y=1情况下的参数,而y=0情况下其实未给出参数,因为y=0的假设函数值可以通过1-(y=1的假设函数值)得到。同理,k分类中参数其实只需要k-1个参数就可以了,多余的一个参数是冗余的。
具体冗余参数有什么负面影响,参考Softmax回归 http://ufldl.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92

 浙公网安备 33010602011771号
浙公网安备 33010602011771号