KMP与AC自动机

字符串匹配的基本方法就是，逐位移动模式串，检查当前位置是否匹配。似乎只有这样才能够不遗漏地检查所有可能匹配上的情况。容易发现，这样做的复杂度是\(O(n\)

KMP

匹配

匹配时，\(i\)指针指向文本串当前位，\(j\)指针指向模式串当前位

如果当前位的文本串与模式串匹配成功，即$T_i = P_j$，两指针同时移动至下一位。

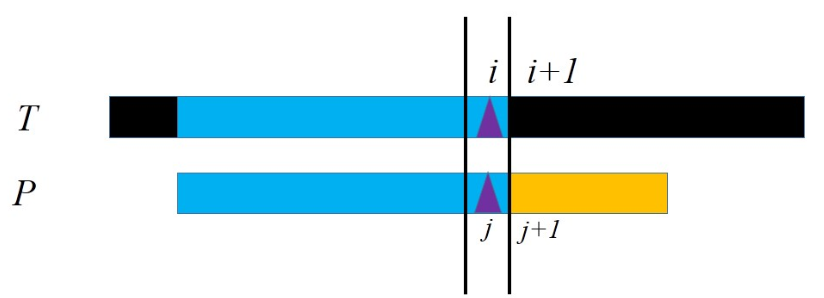
如果当前位文本串与模式串失配，即$T_i \neq P_j$。失配位置之前部分两串都是相同的。我们不移动文本串。当文本串不动而移动模式串时，实际上就是在前面的相同部分里，模式串前缀与文本串后缀匹配的过程。我们要找到模式串在移动过程中，第一个在$i$之前与文本串全部匹配的位置（可能是空），这样才好继续匹配。这等价于模式串$[0,j)$的最长相同前后缀。

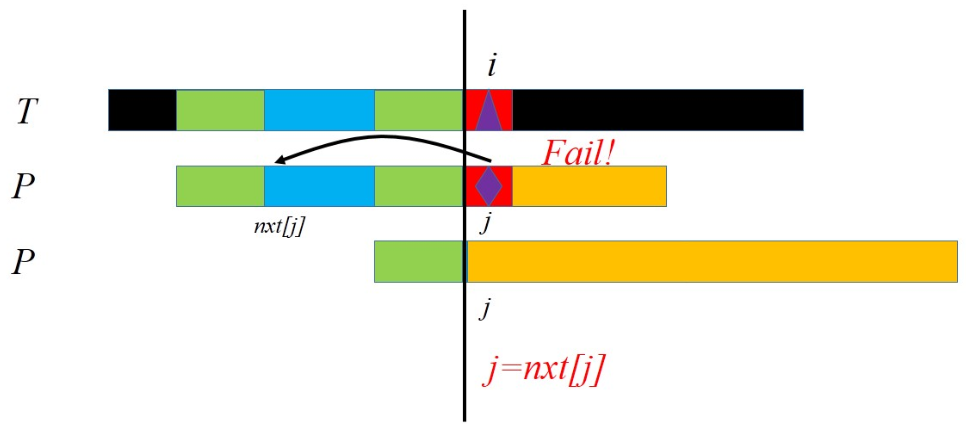
当模式串指针指向$len_p$时，意味着已经找到位置能够让模式串与文本串全部匹配。此时应该与处理方法应当与失配一样，向右移动找到第一个在$i$之前匹配的位置，也就是$j=nxt_j$。

 

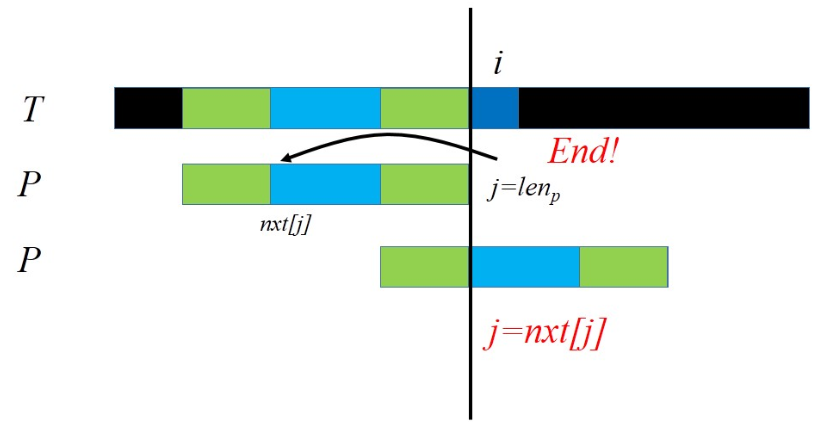
我们注意到整个算法的过程中$i$指针是不会往回移动的，而跳nxt本质上是对逐位移动模式串的一个优化。因此我们总共只做了两个动作，一个是文本串上指针的向右移动，一个是模式串整体的向右移动。总共的移动次数不超过$O(n+m)$。

在学习KMP匹配的过程中，要时常与暴力$O(nm)$做法作比较，得知KMP的正确性。我们使用$nxt_j$跳过一部分匹配，是因为这部分连在$i$之前的部分都不能匹配，必定不用考虑后面的内容。只有当$i$之前匹配，做下去才是有意义的。

$nxt[]$的求解过程

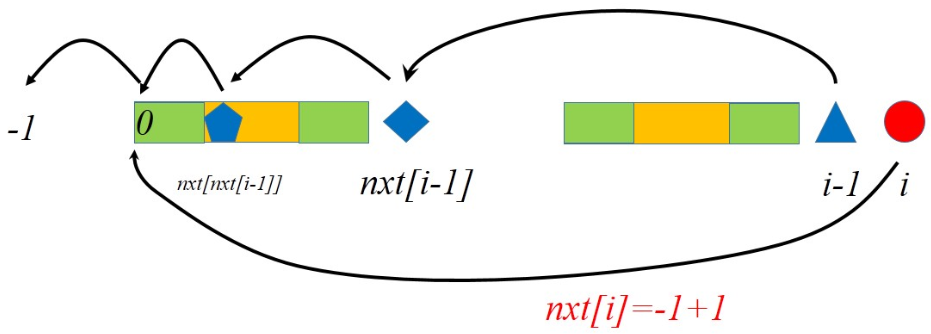
定义：$nxt_i$表示区间$[0,i)$中最长相同前后缀的长度。等价于模式串在$i$位置失配时，应该移动至$nxt_i$处。

求解$nxt_i$时，要利用$nxt_{0~i-1}$的信息。

边界条件：$nxt_0 = -1$

如果$p_{nxt_{i-1}}=p_{i-1}$，利用之前的最长相同前后缀，加上这一位，得到一个最长相同前后缀。

然而如果不相等呢？退而求其次，继续往前迭代，直到找到一个相等的位置为止。

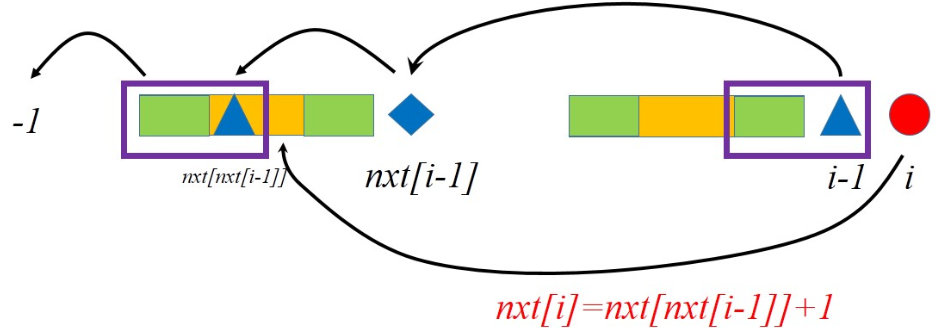
直到找到第一位。这是一个边界条件，我们比较第一位和$i-1$。

进行到这一步说明最长相同前后缀的长度为0。

 

 

AC自动机

多模式串匹配问题，复杂度$O(n+m \cdot L)$

思想：就是KMP。一句话，失配时在所有模式串的前缀里，寻找当前已匹配部分的最长后缀。

由于模式串可能有前后缀关系，匹配成功后需要一直跳$fail$统计。

有一个优化，可以在匹配时不需跳$fail$边（注意是匹配时，不是匹配成功后，成功后如果要优化需要$fail$树）。就是让所有不存在的空儿子点成为$fail$的传送门。这样的AC自动机成为$Trie$图。