公式推导

Monge问题

有两个完备空间\(X,Y\)，概率测度为\(\mu \in P(X),\nu \in P(Y)\)满足\(\mu(X)=\nu(Y)\)，以及传输代价\(c:X \times Y\rightarrow[0,+\infty]\)，需要找到一个映射\(T:X \rightarrow Y\)，诱导推前映射\(T_{\#}\mu=\nu\).

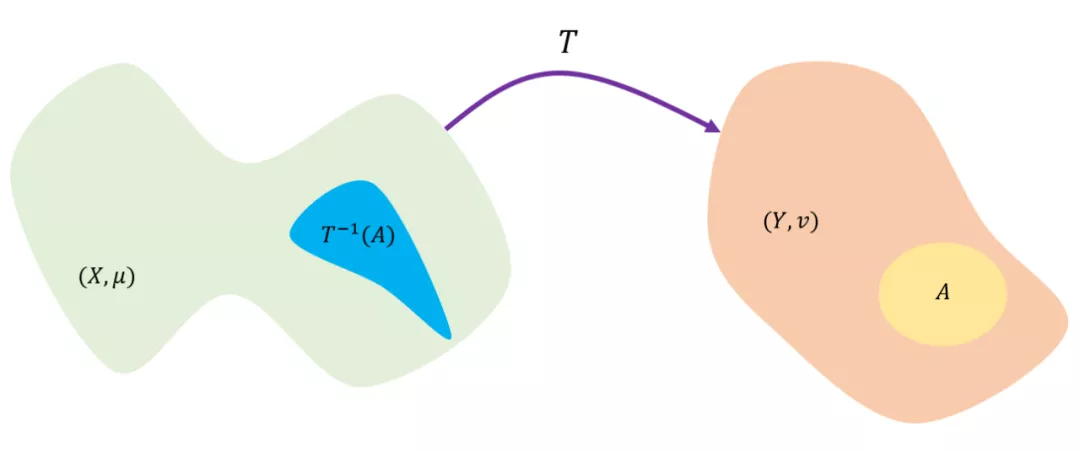
而问题是，\(\forall A \subset Y\)有\(\mu(T^{-1}(A))=\nu(A)\)，满足传输代价\(C(T):\int_Xc(x,T(x))d\mu\)最小。
使用数学语言描述为：\((MP):inf\{M(T):=\int_Xc(x,T(x))d\mu:T_{\#}\mu=\nu\}\).
可以看出，这个问题的解实质上就是最优距离传输，我们将这个最小传输代价定义为Wasserstein距离。
就如同上图所示，Monge 问题其实是在找一个最优传输映射\(T\)，映射\(T\)将空间\(X\)映射为空间\(Y\)，\(A\)是空间\(Y\)中的区域，\(T^{-1}(A)\)是\(A\)在\(X\)中原像。需要满足的条件是对于\(X\)空间中区域 \(T^{-1}(A)\)的测度要与\(Y\)空间中区域\(A\)的测度要相等。测度在上图可以理解为面积相同。
对于 Monge 问题，由于需要求解一个映射，实际上只能允许多对一或者一对一(映射的定义)，Kantorovich将传输映射放松成传输方案，允许一对多，从而将原来问题进行简化。

Kantoroich问题

定义联合概率分布\(\gamma \in P(X \times Y)\)，其边缘概率密度定义为推前映射\((\pi_{x})_{\#}=\int_Y \gamma(x,y)dy\)，\((\pi_{y})_{\#}=\int_X \gamma(x,y)dx\)。
即\(\pi(\mu,\nu)=\{ \gamma \in P(X,Y) : (\pi_{x})_{\#}\gamma = \mu, (\pi_{y})_{\#}\gamma = \nu \}\)，找到一个联合概率分布\(\gamma\)，使得传输代价最小。
即\((KP) inf\{K(\gamma) := \int_{X \times Y}c(x,y)d\gamma(x,y):\gamma\in\pi(\mu, \nu)\}\)
用图形的方式说明，既是：

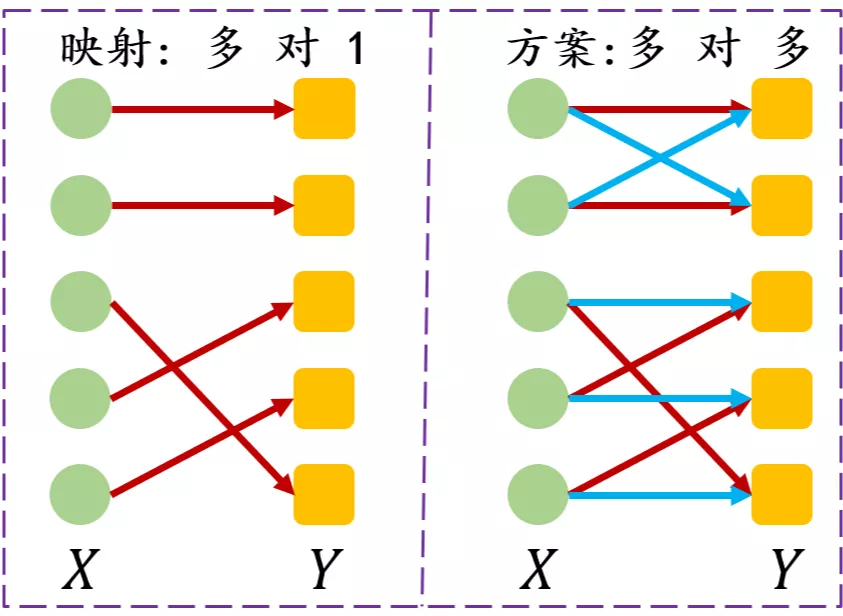
\(KP\)问题很难求解，我们将其推广为对偶问题求解。

对偶问题

\(\gamma \in P(X \times Y)\)，即对\(\forall \varphi \in C(X)\)满足\(\int_X \varphi d\mu = \int_X \varphi d\gamma\)，\(\int_Y \psi d\nu = \int_Y \psi d\gamma\)，因此我们能得到以下推导：
对\(\forall \varphi \in C(X), \psi \in C(Y)\)，满足

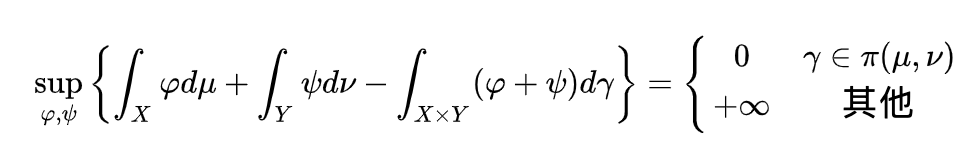
由这个推导可以改写KP问题，

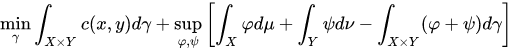
该公式等价于：
\(\underset{\gamma}{min}\int_{X \times Y}c(x,y)d\gamma + \underset{\varphi,\psi}{sup}\int_{X} \varphi d\mu + \underset{\varphi,\psi}{sup}\int_{Y} \psi d\nu - \underset{\varphi,\psi}{sup}\int_{X \times Y} (\varphi+\psi) d\gamma\)
合并相似：
\(\underset{\gamma}{min}\int_{X \times Y}c(x,y)d\gamma - \underset{\varphi,\psi}{sup}\int_{X \times Y} (\varphi+\psi) d\gamma + \underset{\varphi,\psi}{sup}\int_{X} \varphi d\mu + \underset{\varphi,\psi}{sup}\int_{Y} \psi d\nu\)
联合分布，边缘概率函数，\(c \geq \varphi + \psi\)所以能得到最终的对偶问题为：
\(\underset{\varphi,\psi}{sup}\int_{X} \varphi d\mu + \underset{\varphi,\psi}{sup}\int_{Y} \psi d\nu\)
\(=\underset{\varphi,\psi}{sup}\int_{X} \varphi d\gamma + \underset{\varphi,\psi}{sup}\int_{Y} \psi d\gamma\)
\(=\underset{\varphi,\psi}{sup}\int_{X \times Y} \varphi d\gamma + \underset{\varphi,\psi}{sup}\int_{X \times Y} \psi d\gamma\)
\(=\underset{\varphi,\psi}{sup}\int_{X \times Y} \varphi + \psi d\gamma\)
这个问题被称为DP问题。
\(\underset{\varphi,\psi}{sup}\int_{X \times Y} c d\gamma \geq \underset{\varphi,\psi}{sup}\int_{X \times Y} \varphi + \psi d\gamma\)
想要求解DP(传输代价尽可能小)，传输代价C已知。
这里有一个数学概念：C-transform。
给定\(f\)，我们可以轻易得到当前条件下最优的\(g\)，并称之为\((f^{C})_{j}=\underset{i}{min}C_{ij}-f{i}\)。
\(\varphi\)的C-transform就是\(\underset{x}{inf}c(x,y)-\varphi{(x)}\)

这里看不懂