关联速度模型的数学本质探究

今天做题的时候突然发现哈。关联速度这个物理模型的数学诠释。只能向量分解吗？向量分解在这里本质是啥。

前置：

有一个函数 \(y = f(x)\)。
变化率: \(\frac{f(x+ \Delta x) - f(x)}{\Delta x}\)
瞬时变化率(\(f'(x)\) 或 \(\frac{dy}{dx}\))：\(\lim_{\Delta x→0} \frac{f(x+ \Delta x) - f(x)}{\Delta x}\)

这些可以手推，也可以背过啦。。。
幂函数：\(y=f(x)=x^a\)，则\(\frac{dy}{dx}=ax^{a-1}\)。
复合函数也就是\(g(f(x))\)：\(z = g(y), y = f(x),则 \frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}\)。

矢量分解。关联速度模型。

题目：

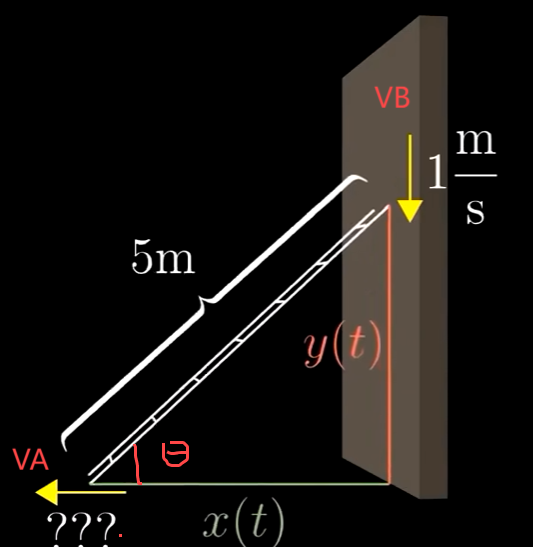
其中，\(y(t)\) 初值 \(4\), \(x(t)\) 初值 \(3\)。如图所示：

物理做法

梯子速度相等啦。

\[V_B sin \theta = V_A cos \theta \]

然后就解出来了。

数学本质

如图所示，时间为 \(t\), 我们把梯子距地面的距离称作 \(x(t)\), 距墙面 \(y(t)\)。
我们想要知道在微小的 \(\Delta t\)下，\(\frac{\Delta x}{\Delta t}\) 的值。这就是瞬时速度的定义呗。

列勾股方程：

\[x(t)^2+y(t)^2=5^2 \]

一个做法，你直接移项变成 \(x(t)\) 的表达式，然后求一下导。但是这特别麻烦。

下面是另一种：
肯定要求变化率，要不然出不来那个 \(\Delta\)。我们对这个表达式求变化率。
那么现在来想一下，对这个表达式求变化率的意义是什么？
你现在把左侧理解为 \(f(t)=x(t)^2+y(t)^2\)。
哦~，这样就有意义了。原来意义就是 \(t\) 的微小变化，表达式的值会改变多少？由于等式右侧为常数，为 \(0\) 吧。
于是都求变化率：

\[2x(t)\frac{d(x(t))}{dt}+2y(t)\frac{d(y(t))}{dt}=0 \]

这一步依据是复合函数的法则，可以多理解理解。
则:$$2(3)\frac{dx}{dt}+2(4)(-1)=0$$

\[\frac{dx}{dt}=\frac{4}{3} \]

联系

假设斜边 \(C\).

\[\sin \theta=\frac{y(t)}{C},\cos\theta=\frac{x(t)}{C} \]

\[V_B=\frac{d(y(t))}{dt},V_A=\frac{d(x(t))}{dt} \]

则我们列的方程就是：

\[\frac{d(y(t))}{dt}\frac{y(t)}{C}=\frac{x(t)}{C}\frac{d(x(t))}{dt} \]

我们已经知道：\(\frac{dy(t)}{dt}\)，\(\tan\theta=\frac{y(t)}{x(t)}\)
你把这个玩意一整理，就是我拿勾股推的那个整理式！！！ 我拿下来哈。

\[2x(t)\frac{d(x(t))}{dt}+2y(t)\frac{d(y(t))}{dt}=0 \]

矢量分解不过是小把戏。真正的意义没那么复杂。他的式子就这么简洁。有些时候他的本质不止向量。

---

或许数学做法十分复杂，但是他给到了一个明确的变化式。这是物理所做不到的。
其实也没那么复杂，你写的话这么写(纯净版)：
列勾股方程：

\[x(t)^2+y(t)^2=5^2 \]

等式两侧求导：

\[2x(t)\frac{d(x(t))}{dt}+2y(t)\frac{d(y(t))}{dt}=0 \]

则:$$2(3)\frac{dx}{dt}+2(4)(-1)=0$$

\[\frac{dx}{dt}=\frac{4}{3} \]

---

就到这里。