最小生成树证明

\(Prim:\)

证明：（人话）：

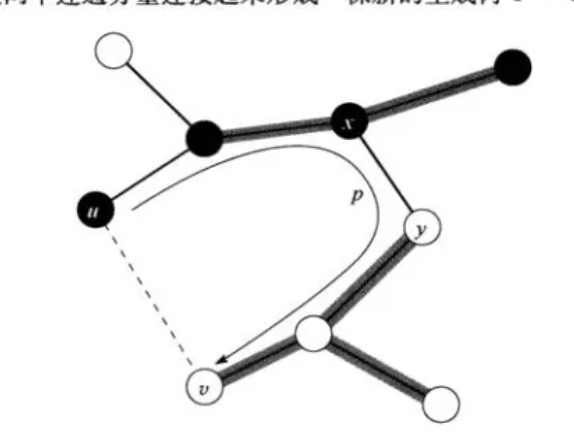
在这个图中 假设当前距离集合最短边是\(u->v\), 那么假设它不在任意一棵最小生成树中
那么 在最小生成树中，\(u -> v\)必然存在其他边相连，并且在这之中，一定存在从集合到外的一条边（横跨切割的边）\(x->y\)，(因为u,v不在一个集合中，如果不存在 那就不可能走出集合)

我们把\(u->v\)换上去，把\(x->y\)换下来，构造生成树。
由于 当前距离集合最短边是\(u->v\),
故 \(w[u->v] <= w[x->y]\)
所以新构造的生成树权值<=最小生成树 故这棵树仍然是最小生成树，
因此加入\(u->v\)一定是在最小生成树中的。（又叫安全边）

\(kruskal:\)

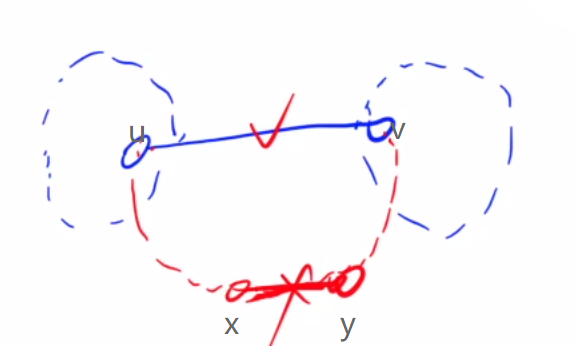
证明：
若不选\(u->v\),
那么 在最小生成树中，\(u -> v\)必然存在其他边相连，并且在这之中，一定存在权值更大\(x->y\)，(因为u,v当前不连通，如果不存在 那就不可能连通)

那么同样构造最小生成树，把\(u->v\)换上去，把\(x->y\)换下来,
权值仍然<=最小生成树权值
说明这是一棵最小生成树。

---

不断加入\(u->v\)，能够保证当前一定是最小生成树的子集。故正确。