寻根KMP算法
\(upd:2025.9.23\) 重写(第五次了
前言
\(KMP\) 算法(\(Knuth-Morris-Pratt\) 算法)是一个著名的字符串匹配算法,效率很高,但是确实有点复杂。
本人被\(KMP\)已经折磨许久。五战KMP。方知之前理解确实浅。故写此篇。
KMP确实是很牛逼的算法。对这个的理解我感觉是循序渐进的过程。在当前阶段,我理解了,实际上还是没有理解到本质,过一段时间再来看,就又加深了许多理解。这大概就是,温故而知新。
字符串下标均从 \(1\) 开始。
匹配
你先写出暴力代码:
for (int i = 1; i <= n; i ++ ) {
bool flag = true;
for (int j = 1; j <= m; j ++ )
if (s[i + j - 1] != p[j]) { flag = false; break; }
if (flag) { ;} //匹配成功
}
假设当前到这就匹配不成功了。 此时 \(s[i+j-1] \neq p[j]\)

暴力做法:

\(i\) 后移一位,\(j\) 直接从头开始匹配。
再往右移:

我们考虑 \(i\) 移动到哪些位置一定是不行的呢?
假如说我们已经知道了最长前后缀长度(最大为 \(j-1\)),我这里记为 \(k\),已经匹配长度记为 \(j\)(图上绿圈到绿线的距离,左闭右开)。
你现在去模拟 \(i\) 往后挪 \(1\) 位,\(2\) 位,\(3\) 位一直挪 \((j - k)\)。
- 当 挪的位数 \(<(j-k)\),由于子串的前后缀都不相等,(最起码到匹配长度为 \(j\))是不可能匹配成功。
- 当 挪的位数 \(=(j-k)\),由于子串的前后缀相等,这个有可能匹配成功,当前匹配长度 \(k\),且 \(i\) 最少挪到这里,才有可能匹配成功。
那我们直接删去这些不可能的 \(i\),令 \(i+=(j-k)\),然后 \(j = k\),继续匹配就行了,注意这里 \(i\) 的含义是起点(跟暴力一样)。
记前 \(i\) 位的最长前后缀长度为 \(d[i]\),我们现在就是:
- 若 \(s[i+j-1] = p[j]\),
j ++ ; - 否则
i+= j - d[j], j = d[j]
这就是 \(KMP\) 的匹配。
是不是我和市面上写法不一样?
我现在要把最长前后缀换一个叫法:\(next[i]\)。代表 使子串 \(s[1…i]\) 有最长相等前后缀的前缀的最后一位的下标。
我们在这里令 \(i'=i+j-1, j' = j\),这样有一个优势,你看代码:
for (int i' = 1, j = 0; i' <= n; i' ++ ) {
while (s[i'] != p[j + 1]) i' = i', j = next[j];
if (s[i'] == p[j + 1]) j ++ ; //这里i' ++ 写在了for 循环里。另外,如果根本就不可能相等,那i++,那么i'++
if (j == m) flag = true; //匹配成功
}
假设我们当前已经求出这个东西。叫做next。
那就容易了。如果蓝圈红圈不匹配,考虑回退,那就回退到next就行了。中间隔下的一定不行,我们知道前后缀不等的,那么一定没法匹配。如果next不行,那就重复这个过程。
代码

\(Next\)
求使前后缀相等的最大长度。略变一下。
强调一下:
\(next\) 数组的含义就是当 j + 1 位失配时,j 应该回退到的位置。
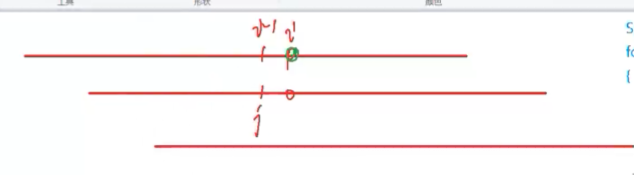
首先,假设现在j在的位置是\(next[i - 1]\)的位置,next[1 ~ i-1]已经求出。
观察\(next[i]\)的性质:
- 使1~i前后缀相等的最大长度 <= 1~ i-1前后缀相等的最大长度+1。这是因为你可以画一下图,如果更大,那就一定不等(1~i-1前后缀已最大),最多扩展i,j+1嘛。
- 其实还是和匹配一样了吧。next[i]肯定要在带上i==j+1的前后缀相等的长度 取最大, 按照暴力思路,你当然会从大到小枚举所有前后缀长度,取第一个行的。实质就是不断右移的过程。
当si!=sj+1时,考虑后退,这个时候又在向右移动了。使前后缀相等,那么回退取值一定只有j,next[j],next[next[j]]....
这是因为你可以任取不在其中的一个数k,那么前后缀就不等了,根本没法匹配。(根据next定义,不在这些不断“最大前后缀相等长度”中,那肯定不等啊)
匹配成功后,j=next[i],重复上述过程。可不就求出来了?

好了那这样就愉快解决了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号