【深度学习数学基础：高等数学】【苏德矿高等数学】第10讲：函数极限性质

3. 函数极限

3.1 函数极限的概念

3.1.1 函数极限定义

【定理】\(\lim\limits_{x\to \infty}f(x)=A\)的充要条件是\(\lim\limits_{x\to +\infty}f(x)=A\)，\(\lim\limits_{x\to -\infty}f(x)=A\)
【证明】先证必要性：
由于\(\lim\limits_{x\to \infty}f(x)=A\)，\(\forall\varepsilon>0,\exists X>0\)，当\(|x|>X\)时，都有\(|f(x)-A|<\varepsilon\)，又因为\(|x|>X\)，即\(x<-X\)或\(x>X\)，即
当\(x<-X\)时，\(|f(x)-A|<\varepsilon\)
当\(x>X\)时，\(|f(x)-A|<\varepsilon\)
即\(\lim\limits_{x\to +\infty}f(x)=A\)，\(\lim\limits_{x\to -\infty}f(x)=A\)
再证充分性：
由\(\lim\limits_{x\to +\infty}f(x)=A\)
\(\forall\varepsilon>0,\exists X_1 > 0\)，当\(x>X_1\)时，都有\(|f(x)-A|<\varepsilon\).
又\(\lim\limits_{x\to -\infty}f(x)=A\)
\(\forall\varepsilon>0,\exists X_2 > 0\)，当\(x< - X_2\)时，都有\(|f(x)-A|<\varepsilon\).
取\(\max\{X_1,X_2\}=X\)，\(X\geqslant X_1,X\geqslant X_2\)，\(-X\leqslant -X_2\)
当\(|x|>X\)时（即\(x<-X\leqslant -X_2\)或\(x>X\geqslant X_1\)），都有\(|f(x)-A|<\varepsilon\)
知\(\lim\limits_{x\to \infty}f(x)=A\)


【推论】【判断\(\lim\limits_{x\to \infty}f(x)=A\)不存在】\(\lim\limits_{x\to +\infty}f(x)=A\)，\(\lim\limits_{x\to -\infty}f(x)=B\)且\(A\ne B\)或二者之一有极限不存在的情况，则\(\lim\limits_{x\to \infty}f(x)\)不存在。

【例】证明\(\lim\limits_{x\to\infty}\frac{1}{x^k},k>0\)且为常数。
【证明】\(\forall\varepsilon>0\)，若要\(|\frac{1}{x^k}-0|<\varepsilon\)成立
\(\Leftrightarrow |\frac{1}{x^k}|=\frac{1}{|x|^k}<\varepsilon\)
两边取倒数
\(\Leftrightarrow |x|^k > \frac{1}{\varepsilon}\)
两边取\(\frac{1}{k}\)次幂
\(\Leftrightarrow |x|>(\frac{1}{\varepsilon})^{\frac{1}{k}}\)，取\((\frac{1}{\varepsilon})^{\frac{1}{k}}>0\)
当\(|x|>X\)时，都有\(|\frac{1}{x^k}-0|<\varepsilon\)
所以\(\lim\limits_{x\to\infty}\frac{1}{x^k},k>0\)且为常数。
【注】\(\lim\limits_{x\to\infty}\frac{1}{\sqrt{x}}=0\)，这也成立，暗含着\(x\geqslant 0\)的情况。

观察下面的图：

当\(x\)趋于\(x_0\)（两边趋近）时，\(f(x)\)确实趋近于\(A\)
研究函数某点有无极限与函数在该点是否有定义没关系
\(x\to x_0\)要求\(x\ne x_0\)，也就是\(x \in \stackrel{o}{U}\left(x_{0}\right)\)（空心邻域，也叫去心邻域）
也就是要保证函数在该点的空心邻域中有定义
从左边趋于\(x_0\)类似趋近于负无穷，从右边趋近于\(x_0\)类似趋近于正无穷
【定义】若\(\exists \delta_0 >0,f(x)\)在\(\stackrel{o}{U}\left(x_{0}\right)\)内有定义，对于\(\forall\varepsilon>0,\exists \delta>0(\delta\leqslant\delta_0)\)（确保\(x_0\)的空心邻域的半径要保证在有定义的邻域内），当\(0<|x-x_0|<\delta\)（\(x \in \stackrel{o}{U}\left(x_{0},\delta\right)\)）时都有\(|f(x)-A|<\varepsilon\)，称\(f(x)\)当\(x\)趋于\(x_0\)时的极限为\(A\)，记作\(\lim\limits_{x\to x_0}f(x)=A\)或\(f(x)\to A(x\to x_0)\).

左右极限

【定义】【右极限】设\(\exists \delta_0>0,f(x)\)在\(\stackrel{o}{U}_{+}\left(x_{0}\right)\)内有定义（右侧邻域，\(x_0\)的右侧，\(x\in(x_0,x_0+\delta_0)\)），\(A\)是一个确定的常数，对于\(\forall\varepsilon>0,\exists\delta>0,\delta\leqslant\delta_0\)，当\(x_0<x<x_0+\delta\)时，都有\(|f(x)-A|<\varepsilon\)，称\(f(x)\)当\(x\)趋于\(x_0\)的右极限是\(A\)，记作\(\lim\limits_{x\to x_{0}^{+}}f(x)=A=f(x_0+o)=f(x_{0}^{+})\)（加小写字母o）.

【注】\(f(x_0+o),(x_{0}^{+})\)表示\(f(x)\)在\(x_0\)的有极限存在，且其值就是\(f(x_0+o),(x_{0}^{+})\).

【定义】【左极限】设\(\exists \delta_0>0,f(x)\)在\(\stackrel{o}{U}_{-}\left(x_{0}\right)\)内有定义，\(A\)是一个确定的常数，对于\(\forall\varepsilon>0,\exists\delta>0,\delta\leqslant\delta_0\)，当\(x_0-\delta<x<x_0\)时，都有\(|f(x)-A|<\varepsilon\)，称\(f(x)\)当\(x\)趋于\(x_0\)的左极限是\(A\)，记作\(\lim\limits_{x\to x_{0}^{-}}f(x)=A=f(x_0-o)=f(x_{0}^{-})\)（加小写字母o）.

【注】\(f(x_0-o),(x_{0}^{-})\)表示\(f(x)\)在\(x_0\)的有极限存在，且其值就是\(f(x_0-o),(x_{0}^{-})\).

【定理】\(\lim\limits_{x\to x_0}f(x)=A\)的充要条件是\(\lim\limits_{x\to x_{0}^{+}}f(x)=A\)且\(\lim\limits_{x\to x_{0}^{-}}f(x)=A\)
【证明】先证必要性：
由于\(\lim\limits_{x\to x_0}f(x)=A\)，\(\exists \delta_0>0,\forall\varepsilon>0,\exists \delta>0(\delta\leqslant\delta_0)\)，当\(0<|x-x_0|<\delta\)（\(x \in \stackrel{o}{U}\left(x_{0},\delta\right)\)）时都有\(|f(x)-A|<\varepsilon\)
当\(x_0<x<x_0+\delta\)时，都有\(|f(x)-A|<\varepsilon\)
当\(x_0-\delta<x<x_0\)时，都有\(|f(x)-A|<\varepsilon\)
即\(\lim\limits_{x\to x_{0}^{+}}f(x)=A,\lim\limits_{x\to x_{0}^{-}}f(x)=A\)
再证充分性：
由于\(\lim\limits_{x\to x_{0}^{+}}f(x)=A\)，则\(\exists \delta_0>0,\forall\varepsilon>0,\exists\delta_1>0,\delta_1\leqslant\delta_0\)，当\(x_0<x<x_0+\delta_1\)时，都有\(|f(x)-A|<\varepsilon\)
由于\(\lim\limits_{x\to x_{0}^{-}}f(x)=A\)，则\(\exists \delta_0>0,\forall\varepsilon>0,\exists\delta_2>0,\delta_2\leqslant\delta_0\)，当\(x_0-\delta_2<x<x_0\)时，都有\(|f(x)-A|<\varepsilon\)
取\(\delta = \min\{\delta_1,\delta_2\}\)，即\(\delta\leqslant\delta_1,\delta\leqslant\delta_2\)，亦即\(-\delta\geqslant -\delta_2\)，当\(0<|x-x_0|<\delta\)时，
即\(x_0-\delta_2 \leqslant x_0-\delta<x<x_0,x_0<x<x_0+\delta\leqslant x_0+\delta_1\)时（去心邻域，不能等于\(x_0\)），都有\(|f(x)-A|<\varepsilon\)
知\(\lim\limits_{x\to x_0}f(x)=A\)

【注1】这是我根据苏老师的口述思路写的证明，欢迎数院大神批评指正。
【注2】这个定理可以用来研究分段函数在分段点的极限是否存在。
【注3】这个定理也可以判断\(f(x)\)在\(x_0\)处极限不存在，见下面的推论。

【推论】【判断\(\lim\limits_{x\to x_0}f(x)=A\)不存在】\(\lim\limits_{x\to x_{0}^{+}}f(x)=A\)，\(\lim\limits_{x\to x_{0}^{-}}f(x)=B\)且\(A\ne B\)或二者之一有极限不存在的情况，则\(\lim\limits_{x\to x_0}f(x)\)不存在。

\(\lim\limits_{x\to x_0}f(x)=A\)的几何意义

\(\forall\varepsilon>0,\exists \delta>0\)，当\(0<|x-x_0|<\delta\)（\(x\in(x_0-\delta,x_o)\cup(x_0,x_0+\delta)\)）时，都有\(|f(x)-A|<\varepsilon\Leftrightarrow A-\varepsilon<f(x)<A+\varepsilon\)

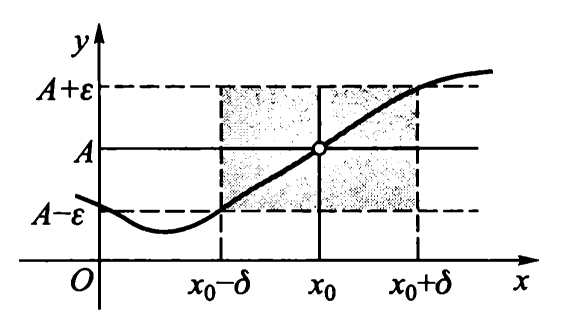
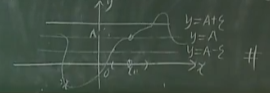
曲线\(y=f(x)\)上的点\((x,f(x))\)全部落在直线\(y=A-\delta\)与\(y=A+\delta\)之间的带形区域内，当\(\varepsilon\)越小，这条“带子”越窄。

例题

【例】证明\(\lim\limits_{x\to x_0}C=C,C\)为常数，\(x_0\)也为常数。
【证明】\(\forall\varepsilon>0\)，取\(\delta=1>0\)，当\(0<|x-x_0|<\delta\)时，都有\(|C-C|=0<\delta\).
所以\(\lim\limits_{x\to x_0}C=C,C\)为常数，\(x_0\)也为常数。

【注】趋于无穷的也是一样，不赘述了。

【例】证明\(\lim\limits_{x\to x_0}x=x_0\).
【证明】\(\forall\varepsilon>0\)，取\(\delta=\varepsilon>0\)，当\(0<|x-x_0|<\delta\)时，都有\(|x-x_0|<\delta=\varepsilon\)
所以\(\lim\limits_{x\to x_0}x=x_0\).

【注】趋于无穷的也是一样，不赘述了，只不过极限不存在，结果是趋向于无穷。

【例】证明\(\lim\limits_{x\to 1}(3x+2)=5\).
【证明】\(\forall\varepsilon>0\)，若要\(|3x+2-5|=|3x-3|<\varepsilon\)成立
\(\Leftrightarrow 3|x-1|<\varepsilon\)
\(\Leftrightarrow |x-1|<\frac{\varepsilon}{3}\)
取\(\delta = \frac{\varepsilon}{3}>0\)
当\(0<|x-1|<\frac{\varepsilon}{3}=\delta\)，都有\(|3x+2-5|<\varepsilon\)
所以\(\lim\limits_{x\to 1}(3x+2)=5\).
< 【注】如果是带分母的复杂形式就要放大不等式。

3.1.2 函数极限的性质

只叙述最难的\(x\to x_0\)的情况（\(\lim\limits_{x\to x_0}f(x),x_0\)为常数）的性质，其他类推
证明和数列极限的性质完全类似，不需要完全掌握证明。

性质1：唯一性

若\(\lim\limits_{x\to x_0}f(x)\)存在，则极限必唯一。

性质2：局部有界性

若\(\lim\limits_{x\to x_0}f(x)=A\)，则\(\exists \delta_0>0\)，当\(x \in \stackrel{o}{U}\left(x_{0},\delta_0\right)\)时，\(|f(x)|\leqslant M,M\)是常数。（在空心邻域内有界）
【证明】由\(\lim\limits_{x\to x_0}f(x)=A\)，取\(\varepsilon=1>0\)，\(\exists\delta_0>0\)，当\(0<|x-x_0|<\delta_0\)时都有\(|f(x)|-|A|\leqslant|f(x)-A|<1\)
\(\Rightarrow |f(x)|<1+|A| \stackrel{\Delta}{=} M\)(这个符号的意思是把\(1+|A|\)记成\(M\))，\(M\)是常数。

性质3：不等式性质

若\(\lim\limits_{x\to x_0}f(x)=A,\lim\limits_{x\to x_0}g(x)=B\)，且\(A<B\)，则\(\exists \delta_0>0\)（\(\delta_0\)的下标0表示半径可以定下来，写\(\delta\)也没关系），当\(0<|x-x_0|<\delta_0\)时，有\(f(x)<g(x)\).

推论

若\(\lim\limits_{x\to x_0}f(x)=A>0\)（\(<0\)），对任何常数\(0<\eta<A\)（\(A<\eta<0\)），\(\exists\delta>0\)（这里不写\(\delta_0\)是因为\(\eta\)不同\(\delta\)也不同），当\(0<|x-x_0|<\delta\)时，都有\(f(x)>\eta>0\)（\(f(x)<\eta<0\)）.

性质4：不等式性质

若\(\exists\delta_0>0\)，当\(0<|x-x_0|<\delta_0\)时，都有\(f(x)\leqslant g(x)\)，且\(\lim\limits_{x\to x_0}f(x)=A,\lim\limits_{x\to x_0}g(x)=B\)，则\(A\leqslant B\).
【证明】用反证法，假设\(A>B\)，由性质3，\(\exists \delta_1>0\)，当\(0<|x-x_0|<\delta_1\)时，有\(f(x)>g(x)\)
取\(\delta = \min\{\delta_0,\delta_1\}\)（与刚才的证明类似，不再赘述），当\(0<|x-x_0|<\delta\)时，\(f(x)\leqslant g(x)\)，也有\(f(x)>g(x)\)，矛盾，则原定理得证。

【注1】条件中\(f(x)\leqslant g(x)\)的等号去掉，结论\(A\leqslant B\)中的等号也不能去掉。
【注2】这也是根据苏老师的口述写的证明，欢迎数院大神批评指正。

性质5：极限的四则运算

若\(\lim\limits_{x\to x_0}f(x)=A,\lim\limits_{x\to x_0}g(x)=B\)，则

• \(\lim\limits_{x\to x_0}(f(x)\pm g(x))=A\pm B\)；
• \(\lim\limits_{x\to x_0}f(x)g(x)=AB\)；
• \(\lim\limits_{x\to x_0}Cf(x)=C\lim\limits_{x\to x_0}f(x),C\)为常数；
• \(\lim\limits_{x\to x_0}\frac{f(x)}{g(x)}=\frac{f(x)}{g(x)},B\ne 0\).

【注】和数列极限一样计算过程中验证。

例题

【例】求\(\lim\limits_{x\to x_0}x^n,n\in\mathbb{N},n\geqslant 2\).
【解】原式\(=\lim\limits_{x \rightarrow x_{0}} \underbrace{x \cdot x \cdots x}_{n \text {个, 有限项 }}\)
\(=\lim\limits_{x\to x_0}x\cdot\lim\limits_{x\to x_0}x\cdots\lim\limits_{x\to x_0}x\)
\(=x_{0}^{n}\).

【例】设\(P_n (x)=a_0x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n\)（此式称为多项式），（\(a_0,a_1,\cdots,a_n\)均为常数），求\(\lim\limits_{x\to x_0}P_n (x)\).
【解】\(\lim\limits_{x\to x_0}P_n (x)=\lim\limits_{x\to x_0}(a_0x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n)\)
\(=\lim\limits_{x\to x_0}a_0x^n+\lim\limits_{x\to x_0}a_1x^{n-1}+\cdots+\lim\limits_{x\to x_0}a_{n-1}x+a_n\)
\(=a_0\lim\limits_{x\to x_0}x^n+a_1\lim\limits_{x\to x_0}x^{n-1}+\cdots+a_{n-1}\lim\limits_{x\to x_0}x+a_n\)
\(=a_0x_{0}^n+a_1x_{0}^{n-1}+\cdots+a_{n-1}x_{0}+a_n\)
\(=P_n(x_0)\).

【注】该多项式的左右极限也是这个值。

【例】设\(Q_m(x)=b_0x^{m}+b_1x^{m-1}+\cdots+b_{m-1}x+b_m\)且\(Q_m(x_0)\ne 0\)，\(P_n(x)\)接上题，求\(\lim\limits_{x\to x_0}\frac{P_n (x)}{Q_m (x)}\).（两个多项式相除称为有理函数）
【解】\(\lim\limits_{x\to x_0}\frac{P_n(x)}{Q_m(x)}=\frac{P_n(x_0)}{Q_m(x_0)}\).

【例】求\(\lim\limits_{x\to \infty}=\frac{a_0x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n}{b_0x^m+b_1x^{m-1}+\cdots+b_{m-1}x+b_m}\)，（\(a_0\ne 0,b_0\ne 0\)且均为常数）。
【解】\(\lim\limits_{x\to \infty} \frac{a_0x^n+a_1x^{n-1}+\cdots+a_{n-1}x+a_n}{b_0x^m+b_1x^{m-1}+\cdots+b_{m-1}x+b_m} = \begin{cases} 0, & n < m \\ \frac{a_0}{b_0}, & n = m \\ \infty, & n > m \end{cases}\).

【注】\(n>m\)情况以后会证明。

【例】求\(\lim\limits_{x\to \infty}\frac{(2x+1)^{20}(3x-2)^{30}}{(5x-6)^{50}}\).
【解】还是用二项展开式，不完全展开
原式\(=\lim\limits_{x\to \infty}\frac{2^{20}3^{30}x^{50}}{5^{50}x^{50}}=\frac{2^{20}3^{30}}{5^{50}}\).

【例】求\(\lim\limits_{x\to 1}\frac{x^2-1}{x^3-1}\).
【解】\(x\to 1,x\ne 1\)，分母不会为0，有零因子，分解出来约分
原式\(=\lim\limits_{x\to 1}\frac{(x-1)(x+1)}{(x-1)(x^2+x+1)}=\lim\limits_{x\to 1}\frac{x+1}{x^2+x+1}=\frac{2}{3}\).

定理

补充一个注释
在实数范围内，当两者均有意义时，\(\sqrt[n]{|f(x)|}\) 与 \(|\sqrt[n]{f(x)}|\) 是相等的，具体分析如下：

• 1. 当 \(n\) 为正奇数时

对于任意实数 \(f(x)\)，\(\sqrt[n]{f(x)}\) 均有意义（奇数根对被开方数的符号无限制），且结果的符号与 \(f(x)\) 一致。

• 左边：\(\sqrt[n]{|f(x)|}\) 中，\(|f(x)|\) 非负，因此结果为非负数（\(\sqrt[n]{|f(x)|} \geq 0\)）。
• 右边：\(|\sqrt[n]{f(x)}|\) 中，\(\sqrt[n]{f(x)}\) 的符号与 \(f(x)\) 一致，取绝对值后结果也为非负数，且等于 \(\sqrt[n]{|f(x)|}\)（例如：\(n=3\)，\(f(x)=-8\) 时，左边 \(\sqrt[3]{|-8|}=\sqrt[3]{8}=2\)，右边 \(|\sqrt[3]{-8}|=|-2|=2\)，相等）。

• 2. 当 \(n\) 为正偶数时

此时 \(\sqrt[n]{f(x)}\) 有意义的前提是 \(f(x) \geq 0\)（偶数根要求被开方数非负），此时：

• 左边：\(\sqrt[n]{|f(x)|} = \sqrt[n]{f(x)}\)（因 \(f(x) \geq 0\)，\(|f(x)|=f(x)\)），结果非负。
• 右边：\(|\sqrt[n]{f(x)}| = \sqrt[n]{f(x)}\)（因 \(\sqrt[n]{f(x)} \geq 0\)，绝对值不改变其值）。
  因此，两者相等。

• 特殊情况说明

当 \(n\) 为偶数且 \(f(x) < 0\) 时，\(\sqrt[n]{f(x)}\) 在实数范围内无意义，此时无法比较两者；但在均有意义的实数范围内，两者必然相等。

• 结论： 在两者均有意义的实数范围内，\(\sqrt[n]{|f(x)|} = |\sqrt[n]{f(x)}|\)。

【前置知识】\(a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+\cdots+b^(n-1))\)
【定理】若\(\lim\limits_{x\to x_0}f(x)=A\geqslant 0\)，则\(\lim\limits_{x\to x_0}\sqrt[n]{f(x)}=\sqrt[n]{A}\).
【证明】当\(A=0\)时，由\(\lim\limits_{x\to x_0}f(x)=A= 0\)，则\(\exists \delta_0>0,\forall\varepsilon>0,\exists\delta>0(\delta\leqslant\delta_0)\)，当\(0<|x-x_0|<\delta\)时，都有\(|f(x)-A|=|f(x)|<\varepsilon\)
不等式两侧同时取\(\frac{1}{n}\)次幂
\(\Leftrightarrow \sqrt[n]{|f(x)|}<\sqrt[n]{\varepsilon}\)
\(\Leftrightarrow |\sqrt[n]{f(x)}|=|\sqrt[n]{f(x)}-0|<\sqrt[n]{\varepsilon}\)
即\(\exists \delta_0>0,\forall\varepsilon>0,\exists \delta>0(\delta\leqslant\delta_0)\)，当\(0<|x-x_0|<\delta\)时\(|\sqrt[n]{f(x)}-\sqrt[n]{A}|<\sqrt[n]{\varepsilon}\)
知\(\lim\limits_{x\to x_0}\sqrt[n]{f(x)}=\sqrt[n]{A}\)
当\(A>0\)时，由\(\lim\limits_{x\to x_0}f(x)=A> 0\)，则\(\exists \delta_0>0,\forall\varepsilon>0,\exists\delta>0(\delta\leqslant\delta_0)\)，当\(0<|x-x_0|<\delta\)时，都有\(|f(x)-A|<\varepsilon\)
由函数极限性质的推论知\(f(x)>0\)

推论
若\(\lim\limits_{x\to x_0}f(x)=A>0\)（\(<0\)），对任何常数\(0<\eta<A\)（\(A<\eta<0\)），\(\exists\delta>0\)（这里不写\(\delta_0\)是因为\(\eta\)不同\(\delta\)也不同），当\(0<|x-x_0|<\delta\)时，都有\(f(x)>\eta>0\)（\(f(x)<\eta<0\)）.

\(|\sqrt[n]{f(x)}-\sqrt[n]{A}|\)
\(= |\frac{(\sqrt[n]{f(x)}-\sqrt[n]{A})((\sqrt[n]{f(x)})^{n-1}+\sqrt[n]{f(x)})^{n-2}\sqrt[n]{A})+\cdots+(\sqrt[n]{A})^{n-1})}{(\sqrt[n]{f(x)})^{n-1}+\sqrt[n]{f(x)})^{n-2}\sqrt[n]{A})+\cdots+(\sqrt[n]{A})^{n-1}}|=|\frac{f(x)-A}{(\sqrt[n]{f(x)})^{n-1}+\sqrt[n]{f(x)})^{n-2}\sqrt[n]{A})+\cdots+(\sqrt[n]{A})^{n-1}}|\)
由于\(f(x)>0\)则
\(\Rightarrow |\frac{f(x)-A}{(\sqrt[n]{f(x)})^{n-1}+\sqrt[n]{f(x)})^{n-2}\sqrt[n]{A})+\cdots+(\sqrt[n]{A})^{n-1}}|<|\frac{f(x)-A}{0+0+\cdots+(\sqrt[n]{A})^{n-1}}|=|\frac{f(x)-A}{(\sqrt[n]{A})^{n-1}}|\)
\(\Rightarrow |\frac{f(x)-A}{(\sqrt[n]{A})^{n-1}}|=|\frac{|f(x)-A|}{|(\sqrt[n]{A})^{n-1}|}|<\frac{\varepsilon}{|(\sqrt[n]{A})^{n-1}|}\)
即\(\exists \delta_0>0,\forall\varepsilon>0,\exists \delta>0(\delta\leqslant\delta_0)\)，当\(0<|x-x_0|<\delta\)时，\(|\sqrt[n]{f(x)}-\sqrt[n]{A}|<\frac{\varepsilon}{|(\sqrt[n]{A})^{n-1}|}\)
知\(\lim\limits_{x\to x_0}\sqrt[n]{f(x)}=\sqrt[n]{A}\)
综上所述，定理得证。

【注】这是我根据苏老师口述的思路写的证明，请数院大神批评指正。

【例】求\(\lim\limits_{x\to 1}\frac{\sqrt{x}-1}{\sqrt[3]{x}-1}\).
【解】进行有理化，用公式\(a^3-b^3=(a-b)(a^2+ab+b^2)\)
原式\(=\lim\limits_{x\to 1}\frac{((\sqrt[3]{x})^2+\sqrt[3]{x}+1)(\sqrt{x}-1)(\sqrt{x}+1)}{((\sqrt[3]{x})^2+\sqrt[3]{x}+1)(\sqrt[3]{x}-1)(\sqrt{x}+1)}\)
\(=\lim\limits_{x\to 1}\frac{((\sqrt[3]{x})^2+\sqrt[3]{x}+1)(x-1)}{(x-1)(\sqrt{x}+1)}\)
\(=\lim\limits_{x\to 1}\frac{(\sqrt[3]{x})^2+\sqrt[3]{x}+1}{\sqrt{x}+1}\)
\(=\frac{3}{2}\).