【自学嵌入式：计算机组成原理】16. 用基础门电路可以搭建任意电路

16. 用基础门电路可以搭建任意电路

逻辑门是构建数字电路的核心单元，其中与门（AND）、或门（OR）、非门（NOT） 是最基础的组件。以下从“基础逻辑门的地位”“复杂门的组合实现”“抽象意义与课程关联”展开说明。

一、基础逻辑门的核心地位

与门、或门、非门是计算机逻辑电路的原子单元，其他所有复杂逻辑门（如异或门、同或门）均可通过这三种基础门的组合实现。这一特性称为逻辑门的完备性，即：

\[\text{任意复杂逻辑} = \text{与门} + \text{或门} + \text{非门的组合} \]

二、复杂门的组合示例（以异或门为例）

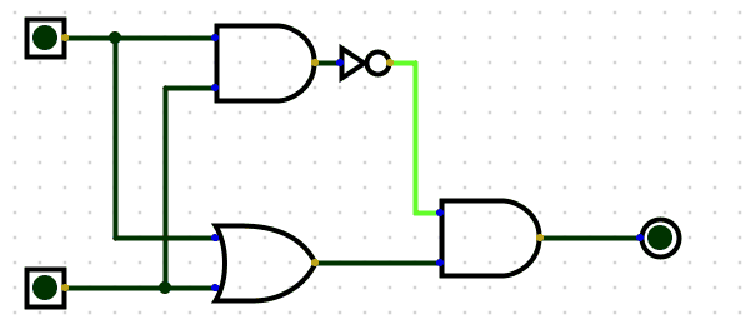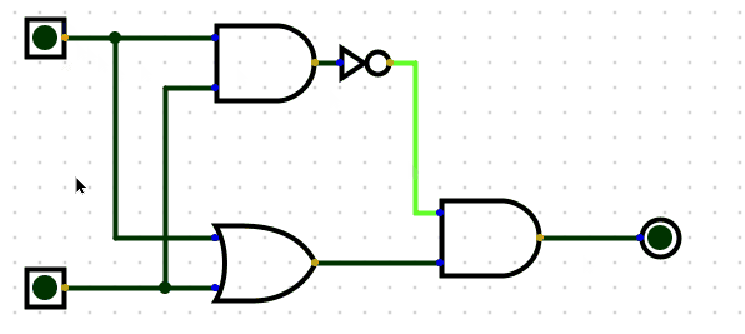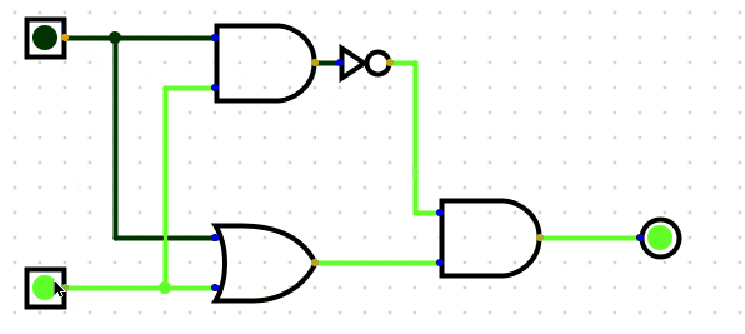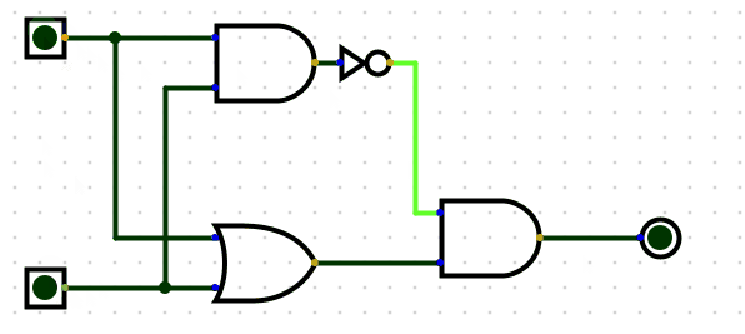
异或门（XOR）的逻辑是“输入不同则输出 1，输入相同则输出 0”，其功能可通过基础门组合实现。以下是核心推导：

（1）异或逻辑的表达式转换

异或的布尔表达式为：

\[C = A \oplus B \]

等价于“或门结果 与 与门非结果”的组合：

\[C = (A \lor B) \land \lnot (A \land B) \]

（2）电路组合示例（对应右侧图示）

1. 第一步：用或门合并输入 \(A\) 和 \(B\)，输出 \(A \lor B\)；
2. 第二步：用与门计算 \(A \land B\)，再通过非门取反，输出 \(\lnot (A \land B)\)；
3. 第三步：用与门将前两步结果合并，最终输出 $ (A \lor B) \land \lnot (A \land B) $，即异或逻辑 $ A \oplus B $。

三、基础逻辑门的抽象意义

基础逻辑门的符号（如与门的“&”、或门的“≥1”、非门的“○”）是继电器电路的抽象简化。通过隐藏底层物理细节（如继电器的电磁控制、布线逻辑），工程师可专注于逻辑组合设计，高效构建复杂电路（如加法器、存储器、CPU控制单元）。

四、数字逻辑课程的作用

大学课程“数字逻辑与逻辑电路”的核心目标是：

• 掌握基础逻辑门的符号、功能与组合规则；
• 学习如何用基础门搭建复杂功能电路（如计数器、译码器、运算单元）；
• 理解计算机硬件的“从简单逻辑到复杂系统”的构建逻辑，为深入学习CPU、芯片设计奠定基础。

总结：与、或、非门是逻辑电路的“基石”，通过组合可实现任意复杂逻辑。理解基础门的抽象意义与组合方法，是掌握数字电路设计、计算机硬件原理的关键起点。