【深度学习数学基础:高等数学】【苏德矿高等数学】第6讲:夹逼定理、单调有界定理
2. 数列极限
2.2 数列极限
2.2.5 收敛数列的性质
推理:保号性
-
若\(\lim\limits_{n\to\infty}a_n=a>0\),对任何常数\(0<\eta<a\)
![image]()
\(\exists N\),当\(n>N\)时,都有\(a_n>\eta>0\).
【证明】取\(b_n=\eta(n=1,2,3,\cdots)\)
\(\lim\limits_{n\to\infty}b_n=\eta\),且\(a>\eta\)
\(\exists N\),当\(n>N\)时,都有\(a_n>b_n\),即\(a_n>\eta>0\)(由上节课的性质3) -
若\(\lim\limits_{n\to\infty}a_n=a<0\),对任何常数\(a<\eta<0\)
\(\exists N\),当\(n>N\)时,都有\(a_n<\eta<0\).
【证明】取\(b_n=\eta(n=1,2,3,\cdots)\)
\(\lim\limits_{n\to\infty}b_n=\eta\),且\(a<\eta\)
\(\exists N\),当\(n>N\)时,都有\(a_n<b_n\),即\(a_n<\eta<0\) (由上节课的性质3)
补充:绝对值的极限
若\(\lim\limits_{n\to\infty}a_n=a\ne 0\),则\(\lim\limits_{n\to\infty}|a_n|=|a|\).
【证明】由于\(\lim\limits_{n\to\infty}a_n=a\ne 0\)
\(\forall\varepsilon>0, \exists N\),当\(n>N\)时,都有\(|a_n-a|<\varepsilon\)
由不等式\(||a|-|b||\leqslant |a\pm b|\leqslant |a|+|b|\)可知
\(||a_n|-|a||\leqslant|a_n-a|<\varepsilon\)
所以\(\forall\varepsilon>0, \exists N\),当\(n>N\)时,都有\(||a_n|-|a||<\varepsilon\)
所以\(\lim\limits_{n\to\infty}|a_n|=|a|\).
性质5:数列极限的四则运算
以下法则要求\(\{a_n\}\)和\(\{b_n\}\)都存在,实际上计算过程中预算,假设它们极限存在,一旦算出来确实存在,就得出结果,如果不存在证明不能拆分,说明这种做法行不通,换一种方法。
-
若\(\lim\limits_{n\to\infty}a_n=a,\lim\limits_{n\to\infty}b_n=b\),则\(\lim\limits_{n\to\infty}(a_n\pm b_n)=\lim\limits_{n\to\infty}a_n \pm \lim\limits_{n\to\infty} b_n=a\pm b\)
-
\(\lim\limits_{n\to\infty}(a_n\cdot b_n)=\lim\limits_{n\to\infty}a_n\cdot \lim\limits_{n\to\infty}b_n=ab\). 特别地,\(C\)为常数,\(\lim\limits_{n\to\infty}(c\cdot a_n)=\lim\limits_{n\to\infty}c\cdot \lim\limits_{n\to\infty}a_n=c\lim\limits_{n\to\infty}a_n\)
-
\(\lim\limits_{n\to\infty}(\frac{a_n}{b_n})=\frac{\lim\limits_{n\to\infty}a_n}{\lim\limits_{n\to\infty}b_n}=\frac{a}{b}\)且\(b\ne 0\).
【证明】由于\(\lim\limits_{n\to\infty}a_n=a,\lim\limits_{n\to\infty}b_n=b\),所以\(\forall\varepsilon>0\),\(\exists N_1, N_2\),当\(n>N_1\)时,有\(|a_n-a|<varepsilon\),当\(n>N_2\)时,有\(|b_n-b|<\varepsilon\),取\(N=\max\{N_1,N_2\}\),则当\(n>N\)时,都有\(|a_n-a|<\varepsilon,|b_n-b|<\varepsilon\),从而有:
(证明加减法)\(|(a_n\pm b_n)- (a\pm b)|=|(a_n- a)\pm (b_n-b)|\leqslant|a_n-a| +|b_n-b|<\varepsilon +\varepsilon = 2\varepsilon\)
所以\(\lim\limits_{n\to\infty}(a_n\pm b_n)=\lim\limits_{n\to\infty}a_n \pm \lim\limits_{n\to\infty} b_n=a\pm b\)
【注】用到了不等式\(|a\pm b|\leqslant |a| + |b|\).
(证明乘法)
\(\begin{aligned}
\left|a_{n} b_{n}-a b\right| & =\left|a_{n} b_{n}-a b_{n}+a b_{n}-a b\right| \\
& =\left|\left(a_{n}-a\right) b_{n}+a\left(b_{n}-b\right)\right| \\
& \leqslant\left|a_{n}-a\right|\left|b_{n}\right|+|a|\left|b_{n}-b\right|,
\end{aligned}\)
由收敛数列的有界性知,存在正数\(M\),对一切\(n\),有\(\left|b_{n}\right| \leqslant M\).于是,
由\(\varepsilon\)的任意性知,\(\lim\limits_{n \rightarrow \infty} a_{n} b_{n}=a b=\lim\limits_{n \rightarrow \infty} a_{n} \cdot \lim\limits_{n \rightarrow \infty} b_{n}\)
(证明除法)
由 \(\lim\limits_{n \rightarrow \infty} b_{n}=b \neq 0\),知 \(\lim\limits_{n \rightarrow \infty}\left|b_{n}\right|=|b|>0\),取 \(0<\eta=\frac{|b|}{2}<|b|\).由保号性知,存在正整数 \(N_{0}\),当 \(n>N_{0}\) 时,有 \(\left|b_{n}\right|>\frac{|b|}{2}\).
取 \(N=\max \left\{N_{0}, N_{2}\right\}\),当 \(n>N\) 时,有 \(\left|b_{n}-b\right|<\varepsilon\),且 \(\left|b_{n}\right|>\frac{|b|}{2}\),则
由 \(\varepsilon\) 的任意性知,\(\lim\limits_{n \rightarrow \infty} \frac{1}{b_{n}}=\frac{1}{b}=\frac{1}{\lim\limits_{n \rightarrow \infty} b_{n}}(b \neq 0)\).
【注意】数列极限的四则运算可以推广到有限项,前提是这些项的极限都存在,不能推广到无限项,反例:\(\lim\limits_{n \to \infty} \underbrace{\frac{1}{n} + \frac{1}{n} + \dots + \frac{1}{n}}_{n个}\),错解为\(=\lim\limits_{n \to \infty}\frac{1}{n}+\lim\limits_{n \to \infty}\frac{1}{n}+\cdots+\lim\limits_{n \to \infty}\frac{1}{n}=0\),实际上原式\(=\lim\limits_{n \to \infty}n \cdot \frac{1}{n}=\lim\limits_{n \to \infty}1=1\),错的原因是无限项不能用,\(n\)趋近于无穷已经变成无限项。
重要公式
由\(\lim\limits_{n \to \infty}\frac{1}{n^k}=0\)(\(k>0\)且为常数)得到下面重要公式
\(\lim\limits_{n \rightarrow \infty} \frac{a_{0} n^{k}+a_{1} n^{k-1}+\cdots+a_{k-1} n+a_{k}}{b_{0} n^{m}+b_{1} n^{m-1}+\cdots+b_{m-1} n+b_{m}}=\left\{\begin{array}{lll}
\infty , & k>m \\
\frac{a_{0}}{b_{0}}, & k=m, \\
0, & k<m ,
\end{array}\right.\),其中\(a_0,a_1,\cdots,a_k,b_0,b_1,\cdots,b_m\)均为常数,\(a_0\ne 0,b_0\ne 0\).
【证明】原式\(=\lim\limits_{n \to \infty}\frac{n^k}{n^m}\cdot\frac{(a_0+a_1\frac{1}{n}+\cdots+a_{k-1}\frac{1}{n^{k-1}}+a_k\frac{1}{n^k})}{(b_0+b_1\frac{1}{n}+\cdots+b_{m-1}\frac{1}{n^{n-m}}+b_m\frac{1}{n^m})}\)
用极限四则运算得
原式\(=\lim\limits_{n \to \infty}\frac{n^k}{n^m}\cdot\frac{a_0}{b_0}=\left\{\begin{array}{lll}
\infty , & k>m \\
\frac{a_{0}}{b_{0}}, & k=m, \\
0, & k<m ,
\end{array}\right.\)
【注】以后会严格证明\(k>m\)极限确实是无穷大。
【注意】分子分母中\(n\)的指数是正数,不要求是自然数,结论依然成立。
【例】\(\lim\limits_{n\to\infty}\frac{n^{2}-100 n+4}{3 n^{2}-90 n+5}=\frac{1}{3}\)
【例】\(\lim\limits_{n\to\infty}\frac{3n^{\frac{4}{3}}-n-1}{4n^4-3n^3+n+1}=0\)
【例】求\(\lim\limits_{n\to\infty}\frac{(2n-1)^{30}(3n+5)^{20}}{4n^{50}-9n^{21}-6}\).
【解】心中默默做二项式展开,知道次方数就行,所以原式\(=\lim\limits_{n\to\infty}\frac{2^{30}n^{30}\cdot 3^{20}n^{20}+\cdots}{4n^{50}-9n^{21}-6}=\frac{2^{30}\cdot 3^{30}}{4}\)
【例】求\(\lim\limits_{n\to\infty}\frac{(1+n)(1+n^2)\cdots(1+n^m)}{3n^{\frac{m(m+1)}{2}}}+6\).
【解】原式\(=\lim\limits_{n\to\infty}\frac{n^{1+2+\cdots+m}+\cdots}{3n^{\frac{m(m+1)}{2}}}+6=\lim\limits_{n\to\infty}\frac{n^{\frac{m(m+1)}{2}}}{3n^{\frac{m(m+1)}{2}}}+6=\frac{1}{3}\)
【例】求\(\lim\limits_{n\to\infty}\frac{1+2+3+\cdots+n}{3n^2-100n+2}\).
【解】原式\(=\lim\limits_{n\to\infty}\frac{\frac{n(n+1)}{2}}{3n^2-100n+2}=\frac{1}{6}\)
2.2.6 判断数列收敛的两个准则
夹逼定理(两边夹定理,迫敛性定理)
【夹逼定理】若\(\exists N_0\),当\(n>N_0\)时,都有\(a_n\leqslant c_n\leqslant b_n\),且\(\lim\limits_{n\to\infty}a_n=a,\lim\limits_{n\to\infty}b_n=a\),则数列\(\{c_n\}\)收敛且\(\lim\limits_{n\to\infty}c_n=a\).
【证明】记\(a_n\leqslant c_n\leqslant b_n...(1)\)
由\(\lim\limits_{n\to\infty}a_n=a\)
\(\forall\varepsilon>0,\exists N_1\),当\(n>N_1\)时,都有\(|a_n-a|<\varepsilon\)
\(\Leftrightarrow a-\varepsilon < a_n < a+\varepsilon...(2)\)
由\(\lim\limits_{n\to\infty}b_n=a\)
\(\forall\varepsilon>0,\exists N_2\),当\(n>N_2\)时,都有\(|b_n-a|<\varepsilon\)
\(\Leftrightarrow a-\varepsilon < b_n < a+\varepsilon...(3)\)
设\(N=\max\{N_0,N_1,N_2\}\),当\(n>N\)时,都有\((1),(2),(3)\)式成立
所以\(a-\varepsilon < a_n \leqslant c_n \leqslant b_n < a+\varepsilon\)
即\(|c_n-a|<\varepsilon\)
所以\(\lim\limits_{n\to\infty}c_n=a\)
【注】若一个数列有很多项相加或相乘,但是不能化简,不能用极限的四则运算,可以尝试用夹逼定理。
【例】求\(\lim\limits_{n\to\infty}\sqrt[n]{a^n+b^n+c^n}\),其中\(a\geqslant b\geqslant c >0\)且为常数。
【解】先放大\(\sqrt[n]{a^n+b^n+c^n}\leqslant \sqrt[n]{3a^n}=a\sqrt[n]{3}\)
\(\sqrt[n]{a^n+b^n+c^n}>\sqrt[n]{a^n}=a\)(其他两项都是大于0的,扔掉它们俩就大于了)
且\(\lim\limits_{n\to\infty}a=a,\lim\limits_{n\to\infty}a\sqrt[n]{3}=a\)
由夹逼定理\(\lim\limits_{n\to\infty}\sqrt[n]{a^n+b^n+c^n}=a\)
【例】求\(\lim\limits_{n\to\infty}(\frac{\sqrt{1\cdot 2}}{n^2+1}+\frac{\sqrt{2\cdot 3}}{n^2+2}+\cdots+\frac{\sqrt{n(n+1)}}{n^2+n})\).
【解】设\(c_n=\frac{\sqrt{1\cdot 2}}{n^2+1}+\frac{\sqrt{2\cdot 3}}{n^2+2}+\cdots+\frac{\sqrt{n(n+1)}}{n^2+n}\)
\(c_n<\frac{\sqrt{1\cdot 2}}{n^2}+\frac{\sqrt{2\cdot 3}}{n^2}+\cdots+\frac{\sqrt{n(n+1)}}{n^2}=\frac{1}{n^2}(\sqrt{1\cdot 2}+\sqrt{2\cdot 3}+\cdots+\sqrt{n(n+1)})\)
\(<\frac{1}{n^2}(2+3+\cdots+(n+1))\)(\(\sqrt{1\cdot 2}<\sqrt{2\cdot 2}=2\),后面以此类推)
\(=\frac{n(n+3)}{2n^2}=\frac{n+3}{2n}\)
\(c_n\geqslant\frac{\sqrt{1\cdot 2}}{n^2+n}+\frac{\sqrt{2\cdot 3}}{n^2+n}+\cdots+\frac{\sqrt{n(n+1)}}{n^2+n}=\frac{1}{n^2+n}(\sqrt{1\cdot 2}+\sqrt{2\cdot 3}+\cdots +\sqrt{n(n+1)})\)(\(n\)取1的时候等号成立,所以带等号,小于可以写成小于等于,但是小于等于不能将等号去掉,大于等于与大于类似)
\(>\frac{1}{n^2+n}(1+2+\cdots+n)=\frac{n(n+1)}{2(n^2+n)}=\frac{1}{2}\)(\(\sqrt{1\cdot 2}>\sqrt{1\cdot 1}=1\),后面以此类推)
由\(\frac{1}{2}<c_n<\frac{n+3}{2n}\),且\(\lim\limits_{n\to\infty}\}\frac{1}{2}=\frac{1}{2}\),\(\lim\limits_{n\to\infty}\frac{n+3}{2n}=\frac{1}{2}\)
由夹逼定理可知\(\lim\limits_{n\to\infty}c_n=\lim\limits_{n\to\infty}(\frac{\sqrt{1\cdot 2}}{n^2+1}+\frac{\sqrt{2\cdot 3}}{n^2+2}+\cdots+\frac{\sqrt{n(n+1)}}{n^2+n})=\frac{1}{2}\)
单调有界定理(原理)
在数学分析中,有7个命题是等价的:
- 戴德金分割原理;
- 确界原理(非空集合,有上界,就有上确界;有下界,就有下确界);
- 单调有界定理(原理);
- 聚点定理;
- 区间套定理;
- 有限覆盖定理;
- 柯西收敛准则;
等价是指,一个成立,其他都成立
这里将单调有界定理作为公理
【单调有界定理】若数列\(\{a_n\}\)递增有上界,则\(\{a_n\}\)收敛;若数列\(\{a_n\}\)递减有下界,则\(\{a_n\}\)收敛,即\(\{a_n\}\)单调且有界,则\(\{a_n\}\)收敛。
【注1】数列递增:\(a_1\leqslant a_2 \leqslant \cdots \leqslant a_n \leqslant \cdots\)
【注2】数列有上界:\(\exists\)常数\(M,\forall n\in\mathbb{N}\),都有\(a_n\leqslant M\)
【注3】数列递减,有下界的概念类比。
【注4】数列递增一定有下界,下界就是第一项;数列递减一定有上界,上界就是第一项。
【注5】定理的条件可减弱为\(\{a_n\}\)当\(n>N_0\)时单调有界,则\(\{a_n\}\)收敛(无限项)(因为改变数列有限项不影响数列的收敛性,比如数列前面有限项是递增的,后面无限项\(n>N_0\)后是递减的且有下界,那就可以用单调有界定理说明数列收敛)
【注6】若\(\{a_n\}\)是由递推关系式给出或者证明\(\{a_n\}\)收敛并求极限,或者直接要求证明\(\{a_n\}\)收敛,或者不能用夹逼定理等(为什么不用夹逼定理、四则运算等其他方法,是因为这种题的极限可能求不出来,但是确实是极限存在(收敛)),这时候尝试用单调有界定理,单调有界定理只能证明收敛,至于求极限,如果数列是由递推关系式给出,先用单调有界定理证明收敛后(一定要先用),极限一般可以求出来,设其极限值为\(A\),利用递推关系式,两边取极限,会得到一个关于\(A\)的方程,把\(A\)解出来即可,其他情况一般不能求出极限,有时候求不出来,在实际工程中,让\(n\)越来越大,越接近,符合精确度约等于即可。

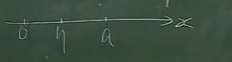

 浙公网安备 33010602011771号
浙公网安备 33010602011771号