【深度学习数学基础:高等数学】【苏德矿高等数学】第3讲:基本初等函数、初等函数和非初等函数
1. 函数
1.7 基本初等函数
1.7.1 常值函数
\(y=C,C\)为某个常数。
- 定义域:\(x\in\mathbb{R}\)(全体实数)
- 图像:
![image]()
1.7.2 幂函数
\(y=x^{\alpha},\alpha\)是常数且\(\alpha\ne 0\).
- 定义域:\(x\in\boldsymbol{D}:\left\{\begin{matrix} \alpha 为自然数, x\in\mathbb R \\ \alpha 为正无理数, x\geqslant 0 \\ \alpha 为负无理数, x>0 \\ \alpha 为负数,有无意义的情况 \end{matrix}\right.\)
- 图像:
![image]()
1.7.3 指数函数
\(y=a^x(a>0,a\ne1为常数)\)
- 定义域\(x\in\mathbb{R}\)
- 图像:
\(a>1\):
![image]()
\(0<a<1\):
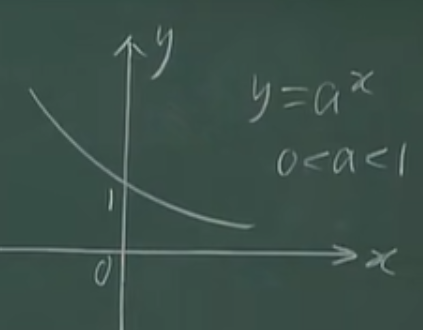
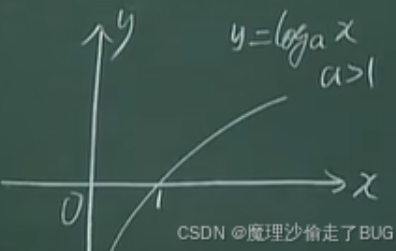
1.7.4 对数函数
\(y=\log_a x,a>0\)且\(a\ne 1\)
- 定义域\(x\in(0,+\infty)\)
- 图像:
\(y=\log_a x,a>1\):
![image]()
\(y=\log_a x,0<a<1\):
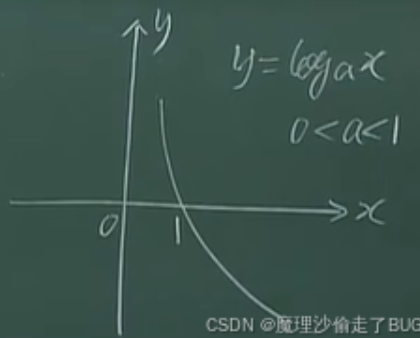
1.7.5 三角函数
假设有如图1.13所示的直角三角形\(\bigtriangleup ABC\),
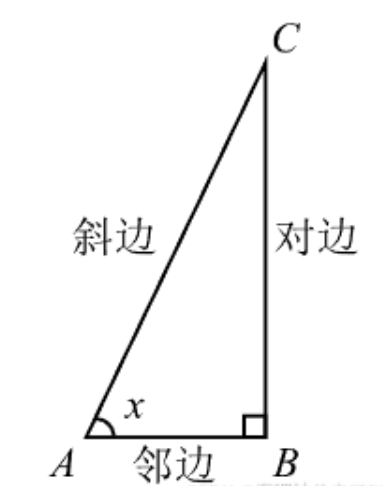
我们将边\(AB\)称为角\(\angle x\)的邻边,将边\(AB\)的长度记为\(|AB|\),将边\(BC\)称为角\(\angle x\)的对边,将边\(BC\)的长度记为\(|BC|\),将边\(AC\)称为角\(\angle x\)的斜边,将边\(AC\)的长度记为\(|AC|\).
1.7.5.1 正弦函数
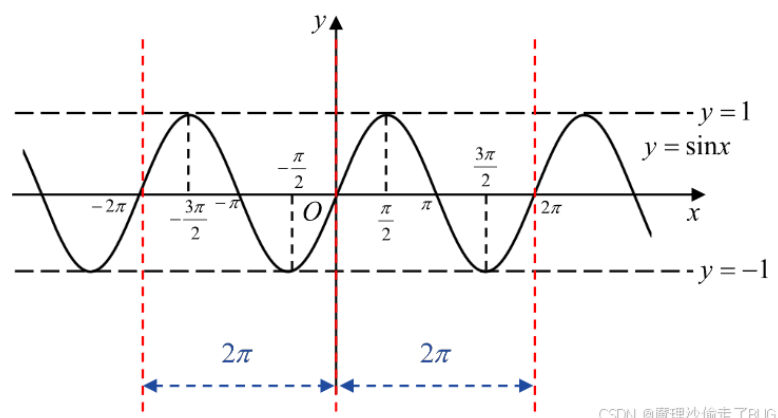
\(y=\sin x=\frac{|BC|}{|AC|}=\frac{对边}{斜边},x\in\mathbb{R},y\in[-1,1]\),其函数图像图如下:
-
正弦函数是奇函数;
-
正弦函数以\(2\pi\)为基本周期;
-
由于\(|\sin x|\leqslant 1\),所以正弦函数有界。
-
特殊函数值:
\[\begin{array}{l} \sin 0=0, \quad \sin \frac{\pi}{6}=\frac{1}{2}, \quad \sin \frac{\pi}{4}=\frac{\sqrt{2}}{2}, \quad \sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}, \\ \sin \frac{\pi}{2}=1, \quad \sin \pi=0, \quad \sin \frac{3 \pi}{2}=-1, \quad \sin 2 \pi=0. \end{array} \]
1.7.5.2 余弦函数
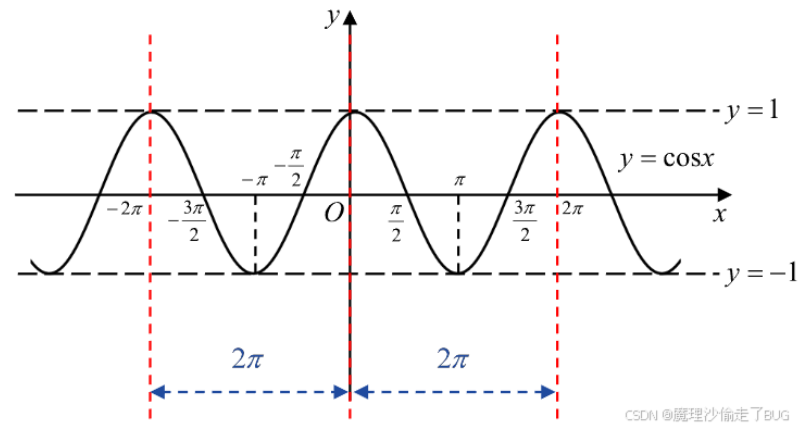
\(y=\cos x=\frac{|AB|}{|AC|}=\frac{邻边}{斜边},x\in\mathbb{R},y\in[-1,1]\),其函数图像图如下:
-
余弦函数是偶函数;
-
余弦函数以\(2\pi\)为基本周期;
-
由于\(|\cos x|\leqslant 1\),所以余弦函数有界。
-
特殊函数值:
\[\begin{array}{l} \cos 0=1, \quad \cos \frac{\pi}{6}=\frac{\sqrt{3}}{2}, \quad \cos \frac{\pi}{4}=\frac{\sqrt{2}}{2}, \quad \cos \frac{\pi}{3}=\frac{1}{2}, \\ \cos \frac{\pi}{2}=0, \quad \cos \pi=-1, \quad \cos \frac{3 \pi}{2}=0, \quad \cos 2 \pi=1. \end{array} \]
1.7.5.3 正切函数
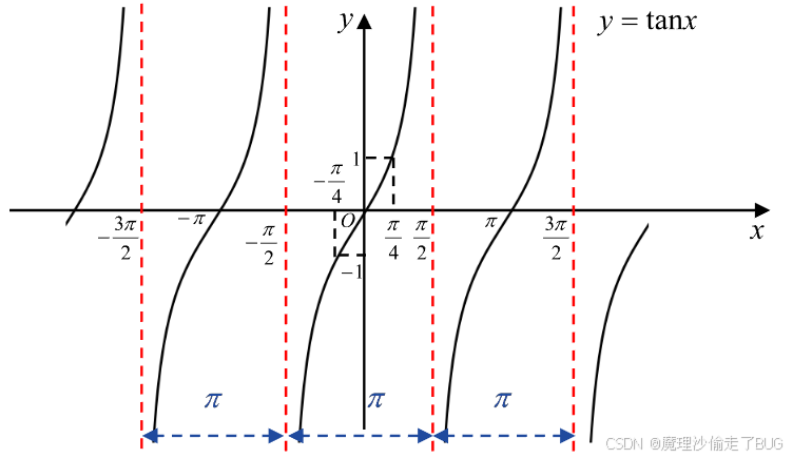
\(y=\tan x=\frac{|BC|}{|AB|}=\frac{对边}{邻边},x\ne k\pi+\frac{\pi}{2},k\in\mathbb{Z},y\in(-\infty,+\infty)\),其函数图像图如下:
-
正切函数在其定义域内是奇函数;
-
正切函数以\(\pi\)为基本周期;
-
特殊函数值:
\[\tan 0=0, \quad \tan \frac{\pi}{6}=\frac{\sqrt{3}}{3}, \quad \tan \frac{\pi}{4}=1, \quad \tan \frac{\pi}{3}=\sqrt{3}. \]
1.7.5.4 余切函数
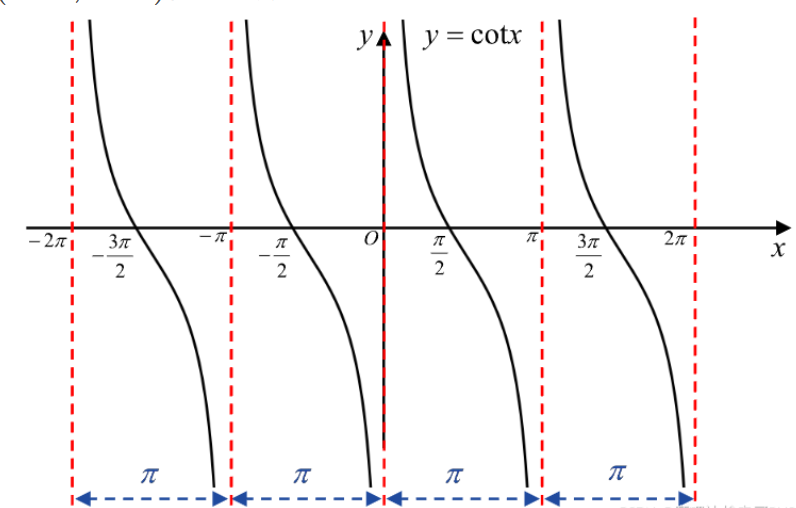
\(y=\cot x=\frac{1}{\tan x}=\frac{|AB|}{|BC|}=\frac{邻边}{对边},x\ne k\pi,k\in\mathbb{Z},y\in(-\infty,+\infty)\),其函数图像图如下:
-
余切函数在其定义域内是奇函数;
-
余切函数以\(\pi\)为基本周期;
-
特殊函数值:
\[\cot \frac{\pi}{2}=0,\cot \frac{3\pi}{2}=0. \]
1.7.5.5 正割函数
\(y=\sec x=\frac{1}{\cos x}=\frac{|AC|}{|AB|}=\frac{斜边}{邻边},x\ne k\pi+\frac{\pi}{2},k\in\mathbb{Z},y\in(-\infty,-1] \cup[1,+\infty)\),其函数图像图如下:
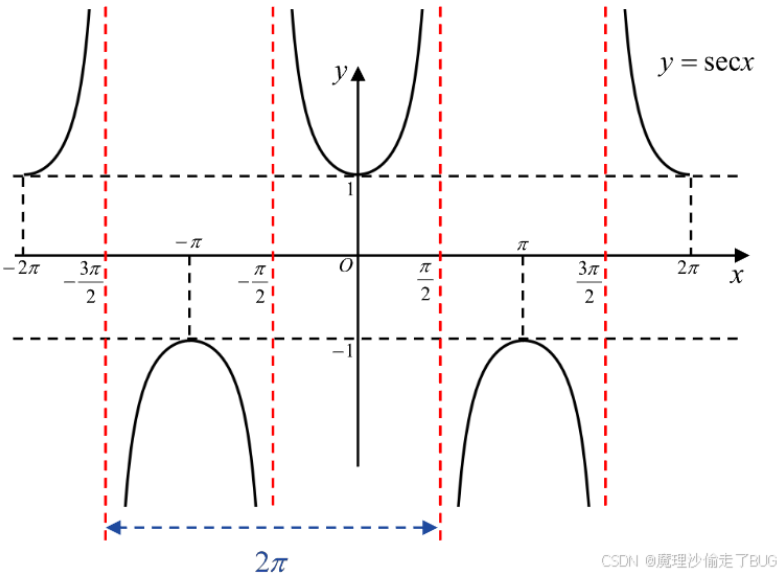
- 正割函数在其定义域内是偶函数;
- 正割函数以\(2\pi\)为基本周期;
- 特殊函数值
1.7.5.6 余割函数
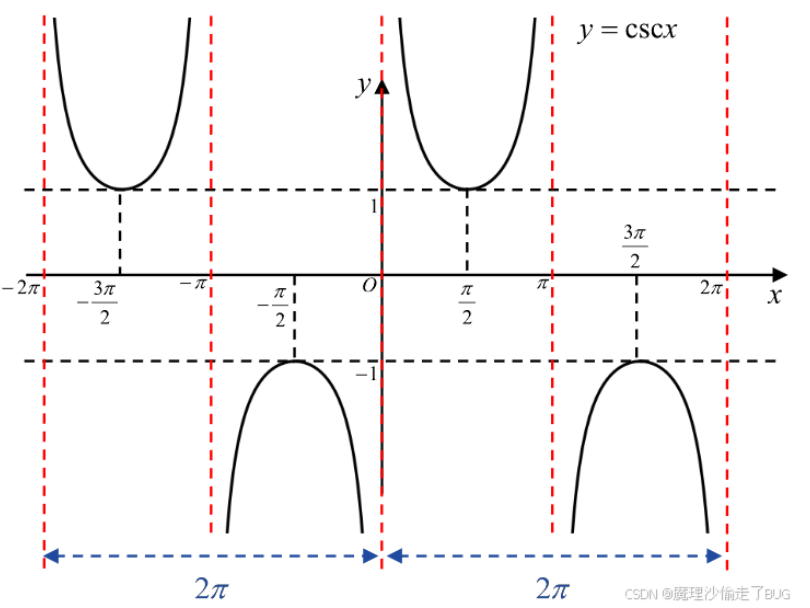
\(y=\csc x=\frac{1}{\sin x}=\frac{|AC|}{|BC|}=\frac{斜边}{对边},x\ne k\pi,k\in\mathbb{Z},y\in(-\infty,-1] \cup[1,+\infty)\),其函数图像图如下:
-
余割函数在其定义域内为奇函数;
-
余割函数以\(2\pi\)为基本周期;
-
特殊函数值:
\[\csc \frac{\pi}{2}=1,\csc\left(-\frac{\pi}{2}\right)=-1 \]
1.7.5.7 三角函数的基本公式
- \(\csc x=\frac{1}{\sin x}\)
- \(\sec x=\frac{1}{\cos x}\)
- \(\cot x=\frac{1}{\tan x}\)
- \(\tan x=\frac{\sin x}{\cos x}\)
- \(\cot x=\frac{1}{\tan x}=\frac{\cos x}{\sin x}\)
- \(\sin ^2 x+\cos^2 x=1\)
- \(1+\tan^2 x=\sec^2 x\)
【证】\(1+\tan^2 x=1+\frac{\sin^2 x}{\cos^2 x}=\frac{\cos^2 x+\sin^2 x}{\cos^2 x}=\frac{1}{\cos^2 x}=\sec^2 x\) - \(1+\cot^2 x=\csc^2 x\)
【证】\(1+\cot^2 x=1+\frac{1}{\tan^2 x}=\frac{\tan^2 x+1}{\tan^2 x}=\frac{\sec^ 2 x}{\tan^2 x}=\frac{\frac{1}{\cos^2 x}}{\frac{\sin^2 x}{\cos^2 x}}=\frac{1}{\sin^2 x}=\csc^2 x\)
1.7.5.8 诱导公式
可用如下口诀将联系记忆起来:“奇变偶不变,符号看象限”。意思为,当\({\displaystyle k}\)为奇数时,\({\displaystyle \sin }\)变为\({\displaystyle \cos }\),\({\displaystyle \cos }\)变为\({\displaystyle \sin }\),\({\displaystyle \tan }\)变为\({\displaystyle \cot }\),\({\displaystyle \cot }\)变为\({\displaystyle \tan }\),\({\displaystyle \sec }\)变为\({\displaystyle \csc }\),\({\displaystyle \csc }\)变为\({\displaystyle \sec }\);而\({\displaystyle k}\)为偶数时,三角函数则不变换。对于正负号,则要看最后角(假设最开始的角在第一象限)所在的象限进行判断,可以使用如下口诀:CAST,也可以使用ASTC (All Students Take Calculus) 用来记忆。
第一象限的 A 即是 All(全部皆正)。
第二象限的 S 即是 Sine & CoSecant(正弦以及余割为正)。
第三象限的 T 即是 Tangent & Cotangent(正切以及余切为正)。
第四象限的 C 即是 Cosine & SeCant(余弦以及正割为正)。
【例】\(\sin(\frac{3}{2}\pi+x)=-\cos x\)(\(\frac{k}{2},k=3\),是奇数,要变化,假设\(x\)对应的角度在第一象限,则\(\frac{3}{2}\pi+x\)在第四象限,第四象限只有余弦和正割是正的,但是本例是正弦函数,所以最后得出\(\sin(\frac{3}{2}\pi+x)=-\cos x\))
1.7.5.9 倍角公式
1.7.5.10 半角公式与降幂公式
1.7.5.11 和差公式
1.7.5.12 积化和差与和差化积公式
1.7.5.13 万能代换公式
1.7.6 反三角函数
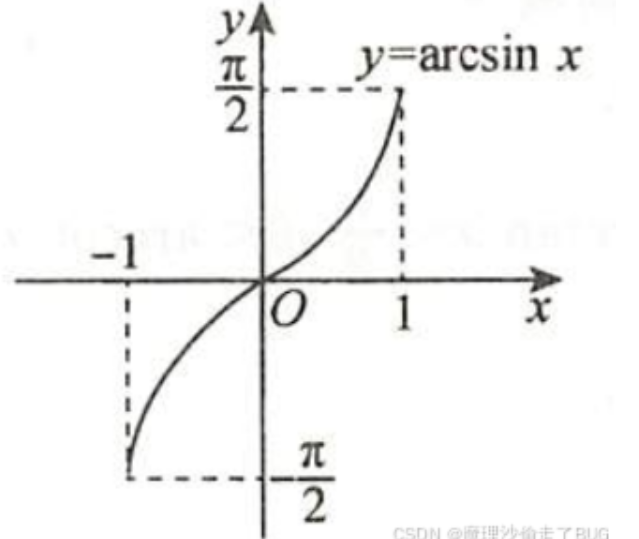
\(y=\sin x,x\in\mathbb{R}\),但是\(y=\sin x,x\in[-\frac{\pi}{2},\frac{\pi}{2}]\)是严格递增函数,因此,\(\sin x\)在此定义域区间内有反函数。记作\(x=\arcsin y\)
1.7.6.1 反正弦函数
\(y=\arcsin x,x\in[-1,1],y\in[-\frac{\pi}{2},\frac{\pi}{2}]\),其图像如下所示(反函数图像(改写字母后)与原函数图像关于\(y=x\)对称):
1.7.6.2 反余弦函数
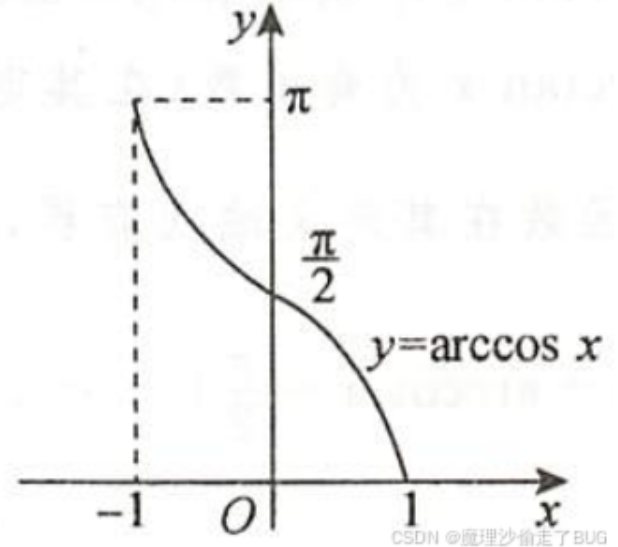
\(y=\cos x,x\in[0,\pi]\)上严格递减,所以在此区间有反函数。
反余弦函数\(y=\arccos x,x\in[-1,1],y\in[0,\pi]\),其图像如下所示:
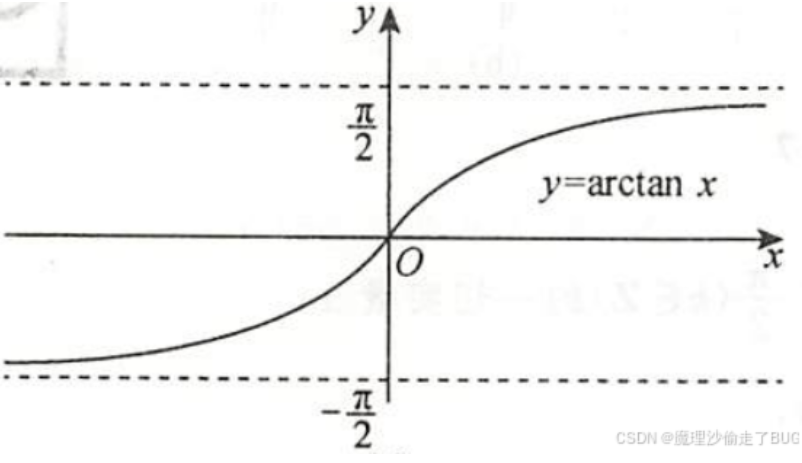
1.7.6.3 反正切函数
\(y=\tan x,x\in(-\frac{\pi}{2},\frac{\pi}{2})\)严格递增,则
反正切函数\(y=\arctan x,x\in\mathbb{R}\),值域\(y\in(-\frac{\pi}{2},\frac{\pi}{2})\),其图像如下所示:
1.7.6.4 反余切函数
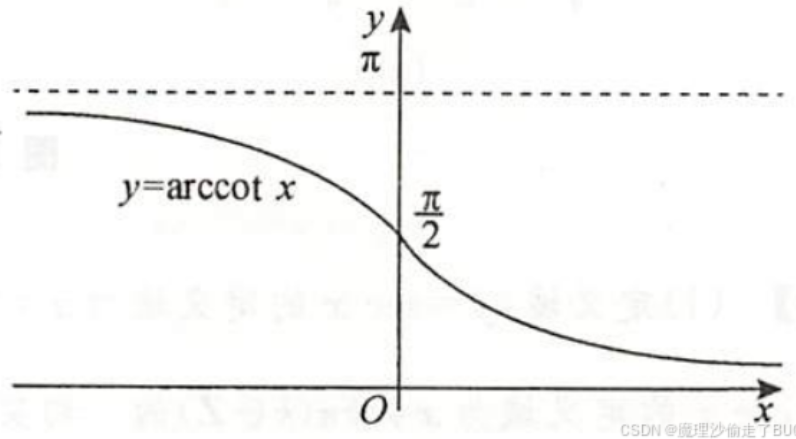
\(y=\cot x,x\in(0,\pi)\)上严格单调递减,所以有反函数
反函数\(y=\text{arccot} x,x\in\mathbb{R},y\in(0,\pi)\),其图像如下所示:
1.7.7 总结
将以上6类函数统称为基本初等函数。
1.8 初等函数
由6种基本初等函数经过有限次四则运算或者复合运算得到的函数就称为初等函数。由6种基本初等函数经过有限次的四则运算(加减乘除)得到的函数称为简单函数。
1.9 非初等函数
不是初等函数的函数称为非初等函数。
- 一般来说分段函数是非初等函数(并非绝对)。
【例】\(f(x)=\left\{\begin{array}{cc} \ln (1+x), & x>0 \\ x^{2}, & x \leqslant 0 \end{array}\right.\)是非初等函数。
【例】\(g(x)=\left\{\begin{array}{cc} \frac{\sin x}{x}, & x\ne0 \\ 1, & x = 0 \end{array}\right.\)是非初等函数。
【例】\(f(x)=\left\{\begin{array}{cc} -x, & x<0 \\ x, & x \geqslant 0 \end{array}\right.\)是初等函数,实际上\(f(x)=|x|=\sqrt{x^2}\),它是由\(y=\sqrt{u},u=x^2\)这两个基本初等函数复合而成的,所以\(f(x)\)是初等函数。
【注】\(x\ne\sqrt{x^2}\),只有当\(x\geqslant 0\)时,\(x=|x|\),所以\(x=|x|=\sqrt{x^2}\),当\(x<0\)时,\(x=-|x|\),所以\(x=-|x|=-\sqrt{x^2}\).
【例】\(y=\frac{\sqrt{\sin x + 1}+x^2+xe^x}{e^{1+\tan x}+x^3+1}\)是不是初等函数?
【解】\(y\)是初等函数,因为它是由\(y=\sin x,y=1,y=\sqrt{x},y=x^2,y=x,y=e^x,y=\tan x,y=x^3\)这些基本初等函数经过8次四则运算复合而成,2次复合运算得到的。
【注】如果这个函数是一个解析式子就是初等函数。(理论上不严谨,必须是我们熟悉的形式)。
一定学会,如果一个函数是复合函数,能拆成几个基本初等函数或简单函数的复合。
【例】\(y=e^{\sqrt{1+\sin \sqrt{x}}}\)是复合函数。它是由\(y=e^u,u=\sqrt{v},v=1+w,w=\sin X,X=\sqrt{x}\)复合而成。
【注】学这些是为了后面学复合函数求导。
1.10 重要的几个函数
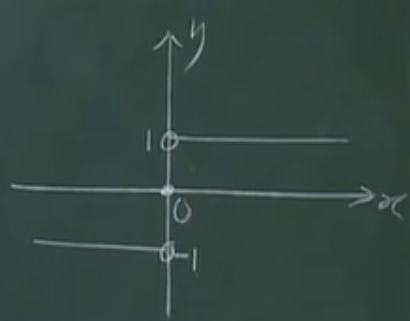
1.10.1 符号函数
\(y=\text{sgn} x=\left\{\begin{array}{cc}
-1, & x<0 \\
0, & x=0 \\
1,&x>0
\end{array}\right.\),其图像如下:
1.10.2 取整函数
记\([x]\)表示不超过\(x\)的最大整数。
【例】\([-3.15]=-4,[\sqrt{2}]=1,[1]=1\).
按照函数的定义,\([x]\)是\(\mathbb{R}\)上的\(x\)的函数,即\(y=[x],x\in\mathbb{R}\).
【不等式】\([x]\leqslant x <[x+1]\)或\(x-1<[x]\leqslant x\)
\(y=[x]=\left\{\begin{array}{cc}
\cdots \\
-1, &-1\leqslant x < 0\\
0, &0\leqslant x < 1\\
1, &1\leqslant x < 2\\
2, &2\leqslant x < 3\\
\cdots \\
\end{array}\right.\)
其函数图像如下所示:

1.10.3 迪利克雷函数
它是一个分段函数
\(D(x)=\left\{\begin{array}{cc}
1, &x为有理数\\
0, &x为无理数\\
\end{array}\right.\)
- 它是周期函数,任何正有理数都是它的周期,所以它没有最小正周期。
- 它没法画出图像。
1.10.4 幂指函数
\(y=u(x)^{v(x)},u(x)\)与\(v(x)\)均是\(x\)的函数且\(u(x)>0\)
若\(A>0,A=a^{\log_a A}(a>0,a\ne 1)\)
特别地\(a=e,A=e^{\log_e A}=e^{\ln A}\)
\(y=u(x)^{v(x)}=e^{\ln u(x)^{v(x)}}=e^{v(x)\ln(u(x))}\)
特别地\(y=x^x=e^{x\ln x}\)


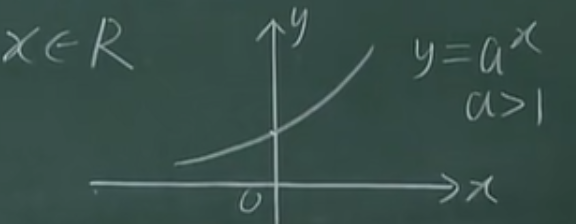

 浙公网安备 33010602011771号
浙公网安备 33010602011771号