【深度学习数学基础：高等数学】【苏德矿高等数学】第1讲：有界函数、无界函数、复合函数

我还是喜欢高数，虽然已经是硕士在读了，但是我还是想再学一遍高数，学高数放松放松（汗流浃背了），笔记就是按视频顺序来的，随缘记录，其实我只是想用学习数学掩盖自己的一些情绪，在最近的生活中，我出现了一些抽象的焦虑情绪，所以我学数学来缓一缓……（数学对我来说是一种“参禅悟道”）
课程地址：https://www.bilibili.com/video/BV1Lt411r7NQ

1. 函数

函数是微积分的研究对象。

1.1 有界函数

在有限的区间上，左端点记为\(N\)，右端点记为\(M\)

1.1.1 下界与上界

【定义】设\(y=f(x),x\in\boldsymbol{D}\)，\(\exists\)常数\(N\leqslant M\)（\(\exists\)表示存在的意思），\(\forall x\in\boldsymbol{D}\)，都有\(N\leqslant f(x) \leqslant M\)（\(\forall\)表示任给一切），称\(f(x)\)是\(\boldsymbol{D}\)上的有界函数，\(N\)称为\(f(x)\)的一个下界（下界有无数个，因为比\(N\)小的数都是它的下界，比\(N\)大的数可能是它的下界可能也不是它的下界），最大的下界称为下确界，\(M\)就称为\(f(x)\)的一个上界（同理上界也有无数个，比\(M\)大的有无数个都是它的上界，比\(M\)小的数也可能是它的上界），最小的上界称为上确界。

1.1.2 有下界函数

\(\exists\)常数\(N\)，\(\forall x\in\boldsymbol{D}\)，都有\(N\leqslant f(x)\)，称\(f(x)\)为有下界函数。

1.1.3 有上界函数

\(\exists\)常数\(M\)，\(\forall x\in\boldsymbol{D}\)，都有\(f(x)\leqslant M\)，称\(f(x)\)为有上界函数。

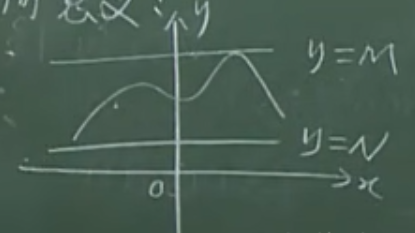
1.1.4 有界函数的几何意义

平面上存在两条直线\(y=N,y=M\)，函数曲线在这连个直线之间（限制住了）。

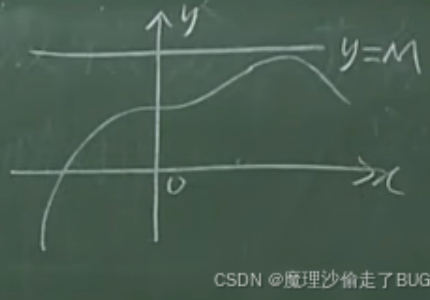
1.1.5 有下界函数的几何意义

存在直线\(y=N\)，函数曲线在该直线的上方。

1.1.6 有上界函数的几何意义

存在直线\(y=M\)，函数曲线在该直线的下方。

1.1.7 函数有界的定义

【定义】\(\exists\)常数\(M>0\)，\(\forall x\in\boldsymbol{D}\)都有\(|f(x)|\leqslant M\Leftrightarrow -M\leqslant f(x)\leqslant M\)，称\(y=f(x)\)在\(\boldsymbol{D}\)上有界。

【补充，绝对值不等式】\(|a\pm b|\leqslant |a|+|b|\)

【例1】证明\(f(x)=\sin ^{80}x - 6 cos^{60} 2x\)有界。
【证】由题意可知，\(f(x)\)的定义域为\(\mathbb{R}\)，
\(|f(x)|=|\sin ^{80}x - 6 cos^{60} 2x|\leqslant|\sin ^{80}x|+| 6 cos^{60} 2x|=\sin ^{80}x|+6|cos^{60} 2x|\leqslant 1+6=7\)
则\(f(x)\)有界。



【补充不等式】

• \(a^2+b^2\geqslant 2ab,ab\leqslant\frac{1}{2}(a^2+b^2)\)，若\(a>0,b>0,\frac{a+b}{2}\geqslant\sqrt{ab}\)
• 更一般地，还有\(n\)个元素的此种不等式：\(\frac{a_{1}+a_{2}+\cdots+a_{n}}{n} \geqslant \sqrt[n]{a_{1} a_{2} \cdots a_{n}}\).

【例2】证明\(f(x)=\frac{x}{1+x^2}\sin x\)有界。
【证】由题意可知，\(f(x)\)的定义域为\(\mathbb{R}\).
\(\forall x\in\mathbb{R},|f(x)|=\frac{|x|}{1+|x|^2}|\sin x|=\frac{|x|\cdot 1}{1+|x|^2}|\sin x|\leqslant\frac{|x|\cdot 1}{1+|x|^2}\leqslant\frac{\frac{1}{2}(|x|^2+1)}{1+|x|^2}=\frac{1}{2}\)
从而\(f(x)\)在\(\mathbb{R}\)上是有界函数。
【注】此题用到的不等式是变种的\(a^2+b^2\geqslant 2ab\Leftrightarrow \frac{1}{2}(a^2+b^2)\leqslant ab\)

1.2 无界函数

数学中经常用到的对立面的词语（反证法常用）：

• \(\forall\)的对立面是\(\exists\)
• \(\exists\)的对立面是\(\forall\)
• \(>\)的对立面是\(\leqslant\)

1.2.1 无界函数

【定义】\(\forall M>0\)，\(\exists x_M\in \boldsymbol{D}\)，但是\(|f(x)|> M\)，则称\(f(x)\)是\(\boldsymbol{D}\)上的无界函数。



【例3】证明\(f(x)=\frac{1}{\sqrt{x}}\)在\((0,1]\)上是无界函数。
【证】（分析法：要证B成立，只要A成立，指的是\(A\Rightarrow B\)，即A成立是B成立的充分条件。）\(\forall M>0\)，若要\(|f(x)|>M\)成立\(\Leftrightarrow|\frac{1}{\sqrt{x}}|>M\Leftrightarrow \frac{1}{\sqrt{x}}>M\Leftrightarrow\frac{1}{x}>M^2\Leftrightarrow0<x<\frac{1}{M^2}\)且\(0<x\leqslant 1\)，取\(x=\frac{1}{(M+1)^2}\in(0,1],0<x<\frac{1}{M^2}\)，有\(|f(x)|>M\)，知\(f(x)\)在\((0,1]\)上是无界的。
【注】取\(x=\frac{1}{(M+1)^2}\)是因为\((M+1)^2>1,M>0\)，此时分母大于1，分子为1，整个分式一定小于1，则\(0<x=\frac{1}{(M+1)^2}<1\)，又因为\((M+1)^2>M^2\)，分母大，整个分式就小了，则\(0<x=\frac{1}{(M+1)^2}<\frac{1}{M^2}\)，所以两个条件均满足。

1.3 复合函数

\(\boldsymbol{D}\)是指定义域，\(\boldsymbol{R}\)是指值域。
【定义】\(y=f(u),u\in\boldsymbol{D}(f)\)，\(u=\varphi (x),u\in\boldsymbol{R}(\varphi)\)且\(\boldsymbol{D}(f)\cap\boldsymbol{R}(\varphi)\ne\emptyset\)，则称\(y=f(\varphi(x))\)为\(x\)的复合函数。

• 由\(\boldsymbol{D}(f)\cap\boldsymbol{R}(\varphi)\ne\emptyset\)，则\(\exists u_0\in\boldsymbol{D}(f)\cap\boldsymbol{R}(\varphi)\Rightarrow u_0\in\boldsymbol{R}(\varphi)\)，\(\exists x_0\)，使得\(u_0=\varphi (x_0),u_0\in\boldsymbol{D}(f)\)，\(u_0\in\boldsymbol{D},\exists y_0\)使得\(y_0=f(u_0)\Rightarrow y_0=f(\varphi(x_0))\)，此时\(x\)称为自变量，\(y\)称为因变量，\(u\)称为中间变量，\(f(u)\)称为外层函数或简称为外函数，\(\varphi(x)\)称为内层函数或简称为内函数。

【反例】\(y=\sqrt{u},u=-(1+x)^2\Rightarrow y=\sqrt{-(1+x^2)}\)，定义域是空集（没有意义），所以复合函数不能是定义域与值域随便复合（微积分都是在实数范围内讨论）。