【深度学习数学基础：线性代数】4. 线性空间及线性映射：4.2 几何解释

4. 特征值特征向量

4.2 几何解释

\(\boldsymbol{A} \boldsymbol{x}\) 是一个线性变换，变换对应的矩阵为 \(\boldsymbol{A}\)。前面介绍过，若 \(\boldsymbol{V}\) 是 \(\{\boldsymbol{x}\}\) 张成的向量空间（此向量空间的维度为1，因为只有一个基向量），那么任意 \(\lambda \boldsymbol{x} \in \boldsymbol{V}\)。所以 \(\boldsymbol{A} \boldsymbol{x} = \lambda \boldsymbol{x}\) 是从 \(\boldsymbol{V}\) 到 \(\boldsymbol{V}\) 自身的映射，\(\boldsymbol{V}\) 也称为 \(\boldsymbol{T}\) 下的不变子空间（求 \(\boldsymbol{A}\) 的特征向量，就是求 \(\boldsymbol{A}\) 的不变子空间）。

若把 \(\boldsymbol{A}\) 看作线性变换系统，\(\boldsymbol{x}\) 就是系统固有的特征，\(\lambda\) 则是该系统对固有特征产生的增益。(增益就是多少倍的意思）

从几何变换的角度来看，如果 \(\boldsymbol{A}\) 是缩放矩阵，\(\boldsymbol{A} \boldsymbol{x}\) 相当于对向量 \(\boldsymbol{x}\) 缩放。在缩放过程中，大部分向量的方向会发生改变，少数特殊向量的方向不变。

【注】

• 通俗理解不变子空间和线性变换系统
  • 1. 先搞懂：什么是线性变换系统？

    • 简单说：线性变换系统就像一台“向量加工机器”，输入一个向量\(\boldsymbol{x}\)，它会按照固定规则（由矩阵\(\boldsymbol{A}\)决定）输出一个新向量\(\boldsymbol{A}\boldsymbol{x}\)。
    • 例子：
      • 缩放机器：输入\(\boldsymbol{x}=(x,y)\)，输出\(\boldsymbol{A}\boldsymbol{x}=(2x,2y)\)（把向量拉长2倍），这里\(\boldsymbol{A}\)是缩放矩阵。
      • 旋转机器：输入\(\boldsymbol{x}=(x,y)\)，输出\(\boldsymbol{A}\boldsymbol{x}=(x\cos\theta-y\sin\theta, x\sin\theta+y\cos\theta)\)（绕原点转\(\theta\)角），这里\(\boldsymbol{A}\)是旋转矩阵。
    • 核心：这个“机器”的规则必须是“线性”的——比如输入\(\boldsymbol{x}+\boldsymbol{y}\)，输出等于\(\boldsymbol{A}\boldsymbol{x}+\boldsymbol{A}\boldsymbol{y}\)；输入\(k\boldsymbol{x}\)（\(k\)是常数），输出等于\(k\boldsymbol{A}\boldsymbol{x}\)。

  • 2. 再理解：什么是不变子空间？

    • 先回忆“子空间”：由一堆向量\(\{\boldsymbol{x}\}\)通过线性组合（比如\(k_1\boldsymbol{x}_1+k_2\boldsymbol{x}_2\)）张成的“向量区域”，比如平面上所有水平向量\((x,0)\)张成的\(x\)轴，就是一个子空间。
    • 不变子空间：如果把这个“向量区域”里的任意向量\(\boldsymbol{x}\)放进线性变换系统\(\boldsymbol{A}\)，输出的\(\boldsymbol{A}\boldsymbol{x}\)仍然在这个区域里，就说这个区域是“\(\boldsymbol{A}\)下的不变子空间”。
    • 例子：
      • 对缩放矩阵\(\boldsymbol{A}=\begin{pmatrix}2&0\\0&3\end{pmatrix}\)，\(x\)轴（子空间\(\{\boldsymbol{x}=(x,0)\}\)）是不变子空间：输入\((x,0)\)，输出\((2x,0)\)，仍在\(x\)轴上。
      • 对特征向量\(\boldsymbol{p}\)：由\(\boldsymbol{p}\)张成的子空间\(V=\{k\boldsymbol{p}\}\)（所有\(\boldsymbol{p}\)的倍数）一定是不变子空间——因为\(\boldsymbol{A}\boldsymbol{p}=\lambda\boldsymbol{p}\)，输出\(\lambda\boldsymbol{p}\)仍在\(V\)里（这就是“求特征向量就是求不变子空间”的原因）。

  • 3. 两者的关系：不变子空间是线性变换系统的“稳定区域”

    • 线性变换系统\(\boldsymbol{A}\)会改变大部分向量的“位置”，但不变子空间里的向量很特殊——无论怎么被\(\boldsymbol{A}\)加工，都不会跑到区域外面。
    • 比如：旋转机器绕\(z\)轴旋转时，\(z\)轴本身（子空间\(\{\boldsymbol{x}=(0,0,z)\}\)）就是不变子空间——不管怎么转，\(z\)轴上的向量方向始终不变，只是可能长度变化（如果有缩放的话）。

  • 4. 一句话总结：

    • 线性变换系统：按矩阵规则加工向量的“机器”；
    • 不变子空间：在这个“机器”加工下，始终保持“内部封闭”的向量区域。

\[\left(\begin{array}{ll} 2 & 0 \\ 0 & 1 \end{array}\right)\left(\begin{array}{lll} 1 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right)=\left(\begin{array}{lll} 2 & 2 & 0 \\ 1 & 0 & 1 \end{array}\right) \]

• 几何变换视角下的特征值与特征向量（以缩放矩阵为例）
  • 1. 缩放矩阵的变换规则
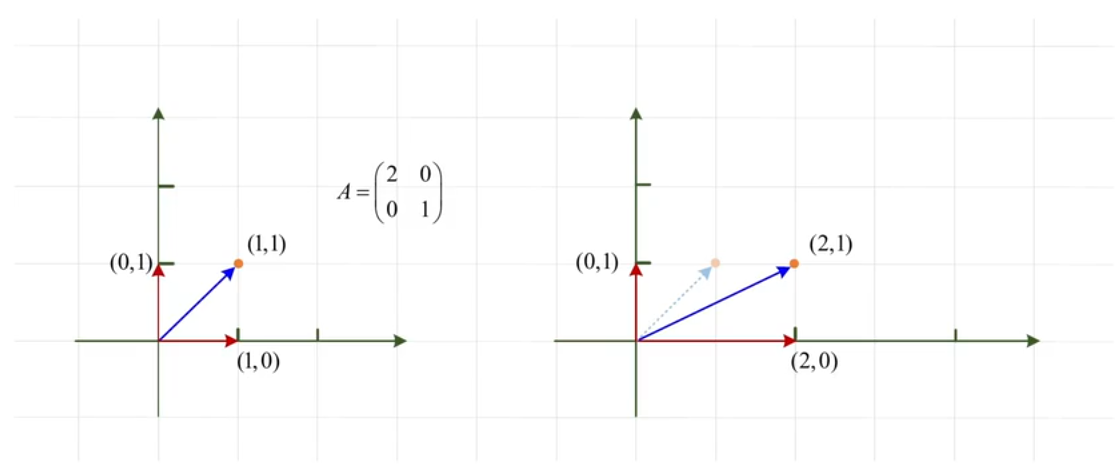
       设缩放矩阵 \(\boldsymbol{A} = \boldsymbol{\begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix}}\)，对二维向量 \(\boldsymbol{x} = \boldsymbol{\begin{pmatrix} x \\ y \end{pmatrix}}\) 的变换为：
    \[\boldsymbol{A}\boldsymbol{x} = \boldsymbol{\begin{pmatrix} 2x \\ y \end{pmatrix}} \]

    几何意义：将向量的 \(x\) 分量放大 2 倍，\(y\) 分量保持不变（即沿 \(x\) 轴方向缩放 2 倍，沿 \(y\) 轴方向缩放 1 倍）。

  • 2. 普通向量的方向变化
       对非特殊向量（如 \(\boldsymbol{x} = \boldsymbol{\begin{pmatrix} 1 \\ 1 \end{pmatrix}}\)），变换后为 \(\boldsymbol{A}\boldsymbol{x} = \boldsymbol{\begin{pmatrix} 2 \\ 1 \end{pmatrix}}\)：
    • 原向量斜率为 \(1\)（\(y = x\)），变换后斜率为 \(\boldsymbol{\dfrac{1}{2}}\)（\(y = \dfrac{x}{2}\)），方向发生明显改变（图中虚线箭头 vs 实线箭头）。
  • 3. 特殊向量的方向不变性
       对 x 轴方向向量（如 \(\boldsymbol{p}_1 = \boldsymbol{\begin{pmatrix} 1 \\ 0 \end{pmatrix}}\)）：
       变换后为 \(\boldsymbol{A}\boldsymbol{p}_1 = \boldsymbol{\begin{pmatrix} 2 \\ 0 \end{pmatrix}} = 2\boldsymbol{p}_1\)，方向仍沿 x 轴（未拐弯），仅长度放大 2 倍。

    对 y 轴方向向量（如 \(\boldsymbol{p}_2 = \boldsymbol{\begin{pmatrix} 0 \\ 1 \end{pmatrix}}\)）：
    变换后为 \(\boldsymbol{A}\boldsymbol{p}_2 = \boldsymbol{\begin{pmatrix} 0 \\ 1 \end{pmatrix}} = 1\boldsymbol{p}_2\)，方向仍沿 y 轴（未拐弯），长度保持不变（放大 1 倍）。

  • 4. 特征值与特征向量的定义
    • 特征向量：变换后 方向不变（仅缩放） 的非零向量（如 \(\boldsymbol{p}_1, \boldsymbol{p}_2\)）。
    • 特征值：缩放的 倍数（\(\boldsymbol{p}_1\) 对应 \(\lambda_1 = 2\)，\(\boldsymbol{p}_2\) 对应 \(\lambda_2 = 1\)）。
      数学表达：若 \(\boldsymbol{A}\boldsymbol{p} = \lambda\boldsymbol{p}\)（\(\boldsymbol{p} \neq \boldsymbol{0}\)），则 \(\boldsymbol{p}\) 是特征向量，\(\lambda\) 是特征值。
  • 5. 几何意义总结
       从几何变换看：
    • 缩放矩阵 \(\boldsymbol{A}\) 会改变 大部分向量的方向（如 \(\boldsymbol{\begin{pmatrix} 1 \\ 1 \end{pmatrix}}\)）；
    • 仅少数 特殊向量（特征向量） 能“抵抗方向变化”，只被拉伸/压缩（如 \(x\) 轴、\(y\) 轴方向的向量）；
    • 特征值描述了这种 拉伸/压缩的力度（正数表示同方向缩放，负数可表示反方向缩放，图中未体现）。

    图中例子直观展现：\(x\) 轴方向是 \(\boldsymbol{A}\) 的“特征方向”，对应特征向量 \(\boldsymbol{p}_1\) 和特征值 \(2\)；\(y\) 轴方向也是“特征方向”，对应特征向量 \(\boldsymbol{p}_2\) 和特征值 \(1\)。

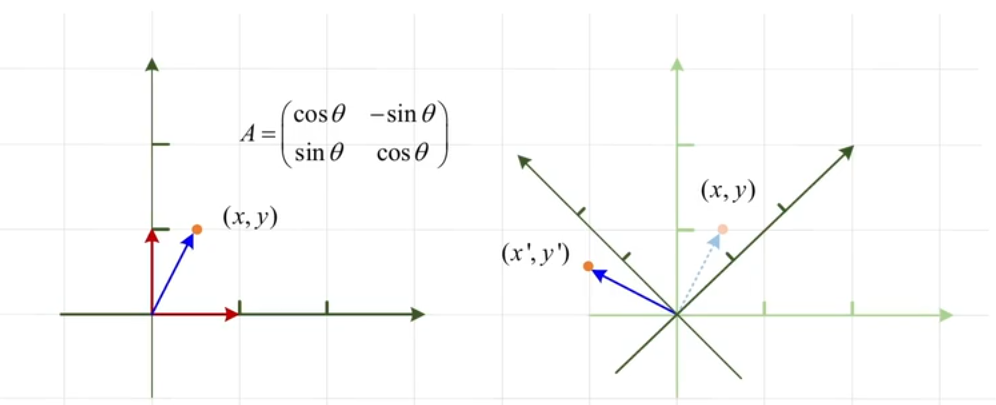
如果把 \(\boldsymbol{A}\) 看作旋转矩阵，如何理解 \(\boldsymbol{A}\boldsymbol{x} = \boldsymbol{x}\) ？若 \(\theta = 2k\pi\)（\(k\) 为整数），所有点都不发生变化；若 \(\theta \neq 2k\pi\)，找不到实数域内方向不变的 \(\boldsymbol{x}\)。这是否意味着 \(\theta \neq 2k\pi\) 时 \(\boldsymbol{A}\) 找不到特征值和特征向量？

答：特征值、特征向量依然存在，只不过是在 复数域 中。通过特征方程推导：

\[\begin{align*} |\boldsymbol{A} - \lambda \boldsymbol{I}| &= \left| \boldsymbol{\begin{pmatrix} \cos\theta - \lambda & -\sin\theta \\ \sin\theta & \cos\theta - \lambda \end{pmatrix}} \right| = 0 \\ \implies (\cos\theta - \lambda)^2 + \sin^2\theta &= 0 \\ (\cos\theta - \lambda)^2 &= -\sin^2\theta \\ \lambda &= \cos\theta \pm i\sin\theta \quad (\text{其中 } i^2 = -1) \end{align*} \]

\[\left(\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)\binom{x}{y}=\lambda\binom{x}{y} \]