【深度学习数学基础：线性代数】3. 线性空间及线性映射：3.4 仿射子集

3. 线性空间及线性映射

3.4 仿射子集

若 \(\boldsymbol{V}\) 是向量空间且 \(\boldsymbol{U}\) 是 \(\boldsymbol{V}\) 的子空间，有 \(\boldsymbol{v} \in \boldsymbol{V}\)（\(\boldsymbol{v}\) 可以属于 \(\boldsymbol{U}\) 也可以不属于 \(\boldsymbol{U}\)），则称 \(\boldsymbol{v} + \boldsymbol{U}\) 是 \(\boldsymbol{V}\) 的仿射子集。称仿射子集 \(\boldsymbol{v} + \boldsymbol{U}\) 平行于 \(\boldsymbol{U}\)。

注意：仿射子集不一定是子空间，因为它不一定包含 \(\boldsymbol{0}\) 元，也不一定满足封闭性。

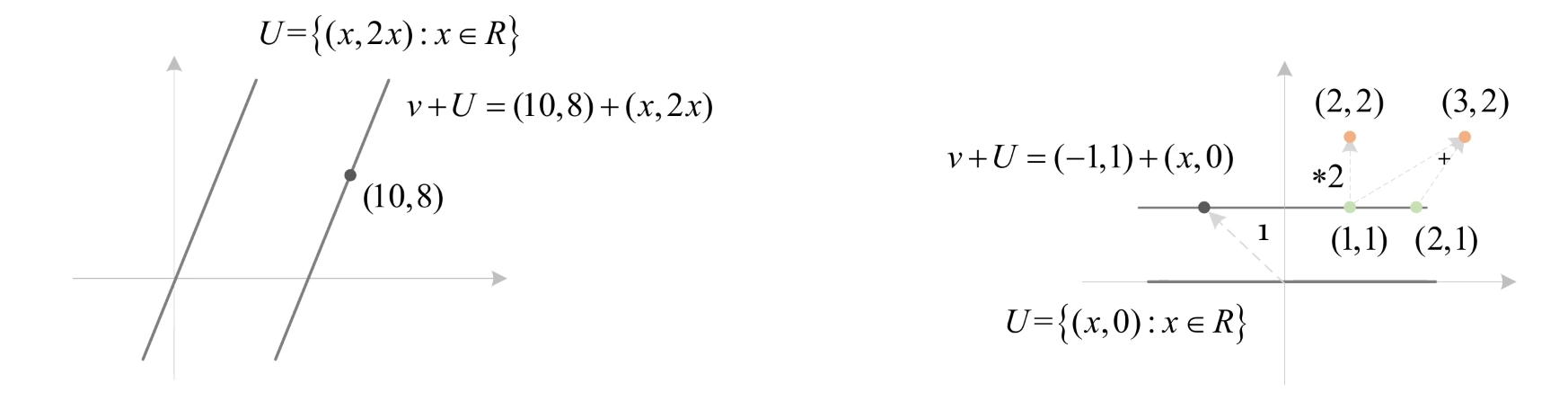
• 仿射子集的几何示例解读

  • 左图：斜率为2的直线平移

    • 子空间 \(\boldsymbol{U}\)：\(\boldsymbol{U} = \left\{ (x, 2x) \mid x \in \mathbb{R} \right\}\)，是 \(\mathbb{R}^2\) 中 过原点、斜率为2的直线（满足子空间封闭性，包含 \(\boldsymbol{0}=(0,0)\)）。
    • 向量 \(\boldsymbol{v}\)：取 \(\boldsymbol{v} = (10, 8)\)（不属于 \(\boldsymbol{U}\)，因 \(2 \times 10 = 20 \neq 8\)）。
    • 仿射子集 \(\boldsymbol{v+U}\)：所有形如 \((10+x,\ 8+2x)\) 的向量，几何上是 将 \(\boldsymbol{U}\) 沿 \(\boldsymbol{v}\) 平移的直线（过 \((10,8)\)，斜率仍为2，与 \(\boldsymbol{U}\) 平行）。
    • 为何不是子空间？
      • 不包含 \(\boldsymbol{0}\)：若 \((a,b)=(0,0)\)，则 \(10+x=0 \Rightarrow x=-10\)，但 \(8+2x=-12 \neq 0\)，矛盾；
      • 不满足封闭性：如子集中 \((10,8)\) 和 \((11,10)\) 相加得 \((21,18)\)，代入 \(\boldsymbol{v+U}\) 得 \(8+2x=18 \Rightarrow x=5\)，但 \(10+x=15 \neq 21\)，故和不在子集中。

  • 右图：水平直线的平移

    • 子空间 \(\boldsymbol{U}\)：\(\boldsymbol{U} = \left\{ (x, 0) \mid x \in \mathbb{R} \right\}\)，即 \(\mathbb{R}^2\) 的 x轴（子空间，含 \(\boldsymbol{0}\)，对运算封闭）。
    • 向量 \(\boldsymbol{v}\)：取 \(\boldsymbol{v} = (-1, 1)\)（不属于 \(\boldsymbol{U}\)，因y坐标为1≠0）。
    • 仿射子集 \(\boldsymbol{v+U}\)：所有形如 \((-1+x,\ 1+0)\) 的向量，即 y=1的水平直线（与x轴平行，方向由 \(\boldsymbol{U}\) 决定）。
    • 为何不是子空间？
      • 不包含 \(\boldsymbol{0}\)：y=1，显然 \((0,0)\) 不在此直线；
      • 不满足封闭性：如 \((2,1)\) 和 \((3,1)\) 相加得 \((5,2)\)，y=2≠1，故和不在子集中；数乘2时，\(2 \times (2,1) = (4,2)\) 也不在子集中。

  • 核心结论
    仿射子集 \(\boldsymbol{v+U}\) 是 子空间 \(\boldsymbol{U}\) 沿 \(\boldsymbol{v}\) 平移的结果，几何上与 \(\boldsymbol{U}\)“平行”，但因不含 \(\boldsymbol{0}\)、不封闭，故不一定是向量空间。