[Acwing蓝桥杯DP] 1078. 旅游规划

题目链接：1078. 旅游规划 - AcWing题库

题目大意:  求一个树上，直径上的所有的点

数据范围：节点n    1<=n<=2e5

范围很大 要求时间复杂度控制在 lnn 以内

分析：

这是一个树形DP，基于树的直径，求树所有直径上的点

整体思路：

1、先通过树形dp求出每个点往下走的最大长度和次大长度，并且更新整棵树的最大路径maxx

2、往下走最大值（第一步已求） + 往上走最大值 == maxx，即在直径上

这个题的难点就是：

首先要理解为什么一个节点既要往上求，又要往下求？

因为第一次dfs时候，回溯时候，是从下往上的，先求下面的点，再上边的

借助y总画的图容易理解

 

 

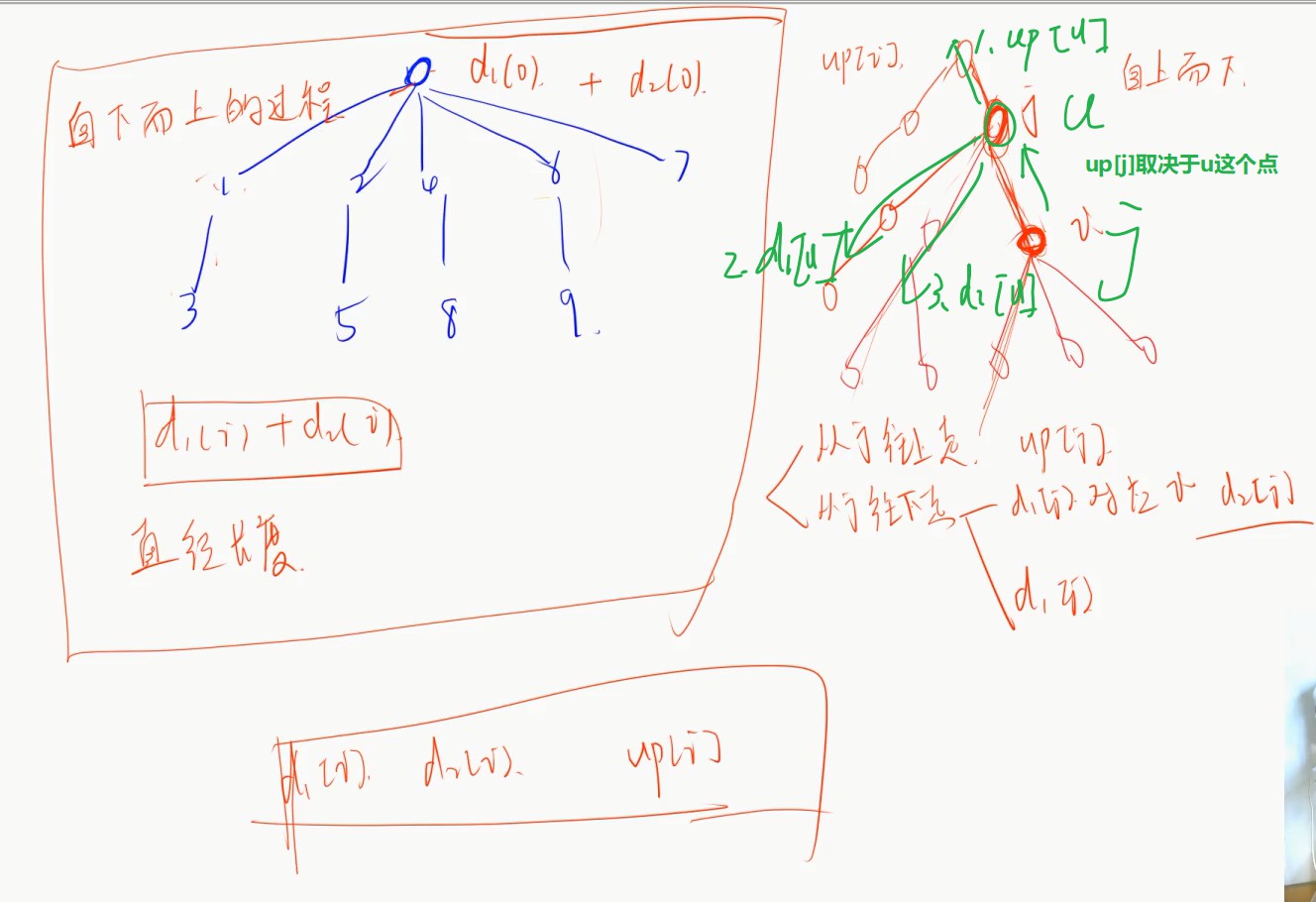
还有就是理解那三个数组：d1往下最大值 d2往下的次大值 up是往上的最大值（实际上就是配合p数组，求最大值）

 

还有就是p数组的理解: p[u]=j :从u下去是j  。

 

比如一个点 i 往下的最大值和次大值是确定的，往上不确定，往上是递归，这里的往上也不是严格意义的往上，是相较与上次递归向下而言的，也有可能向下。

 

这个p数组就是为了防止向下时候最大值算两边，如果是最大值就取次小值。反正这个up值是一直取最大的。

 

看代码：

 

 

#include <bits/stdc++.h>

using namespace std;

const int N=2e5+10,M=2*N;

int n;
int h[N],e[M],ne[M],idx;
int d1[N],d2[N],p[N],up[N];
int maxx;

void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs1(int u,int father)
{
    for(int i=h[u];~i;i=ne[i])
    {
        int j=e[i];
        if(j!=father)
        {
            dfs1(j,u);
            int d=d1[j]+1;
            if(d>d1[u])
            {
                d2[u]=d1[u];
                d1[u]=d;
                p[u]=j;
            }else if(d>d2[u])
            {
                d2[u]=d;
            }
        }
    }
    maxx=max(maxx,d1[u]+d2[u]);
}

void dfs2(int u,int father)
{
    for(int i=h[u];~i;i=ne[i])
    {
        int j=e[i];
        if(j!=father)
        {
            up[j]=up[u]+1;
            if(p[u]==j)
            {
                up[j]=max(up[j],d2[u]+1);
            }else
            {
                up[j]=max(up[j],d1[u]+1);
            }
            dfs2(j,u);
        }
    }
}

int main()
{
    memset(h,-1,sizeof (h));
    cin>>n;
    for(int i=0;i<n;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        add(b,a);
    }
    
    dfs1(0,-1);
    dfs2(0,-1);
    
    for(int i=0;i<n;i++)
    {
        int a[3]={d1[i],d2[i],up[i]};
        sort(a,a+3);
        if(a[2]+a[1]==maxx)
        {
            cout<<i<<endl;
        }
    }
    
    return 0;
}

 

 

 

 

END！！！