【数学建模】建模-整数规划问题

目录

一 整数规划模型（IP）

二 整数规划分类

三 整数规划特点

四 整数规划举例

1 合理下料问题

2 建厂问题

五 整数规划数学模型

六 整数线性规划与线性规划的关系

七 整数线性规划的求解方法

---

一 整数规划模型（IP）

二 整数规划分类

 

三 整数规划特点

四 整数规划举例

1 合理下料问题

 

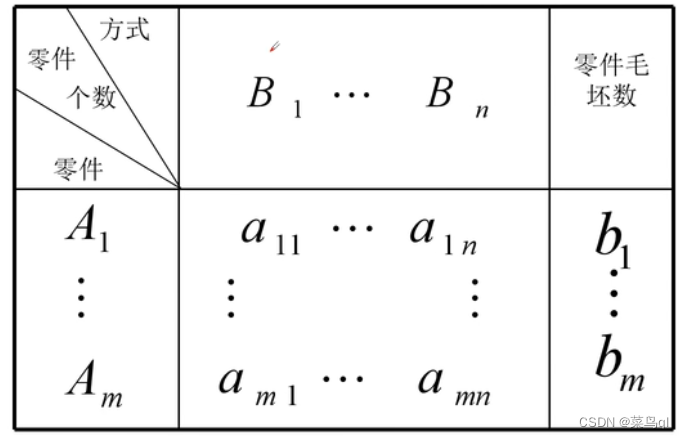
 解：设xj表示用Bj种方式下料的圆钢根数，j=1,2,...,n

 建模：
             n
minZ =  ∑  xj
            j=1

 

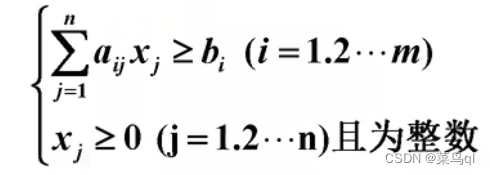
2 建厂问题

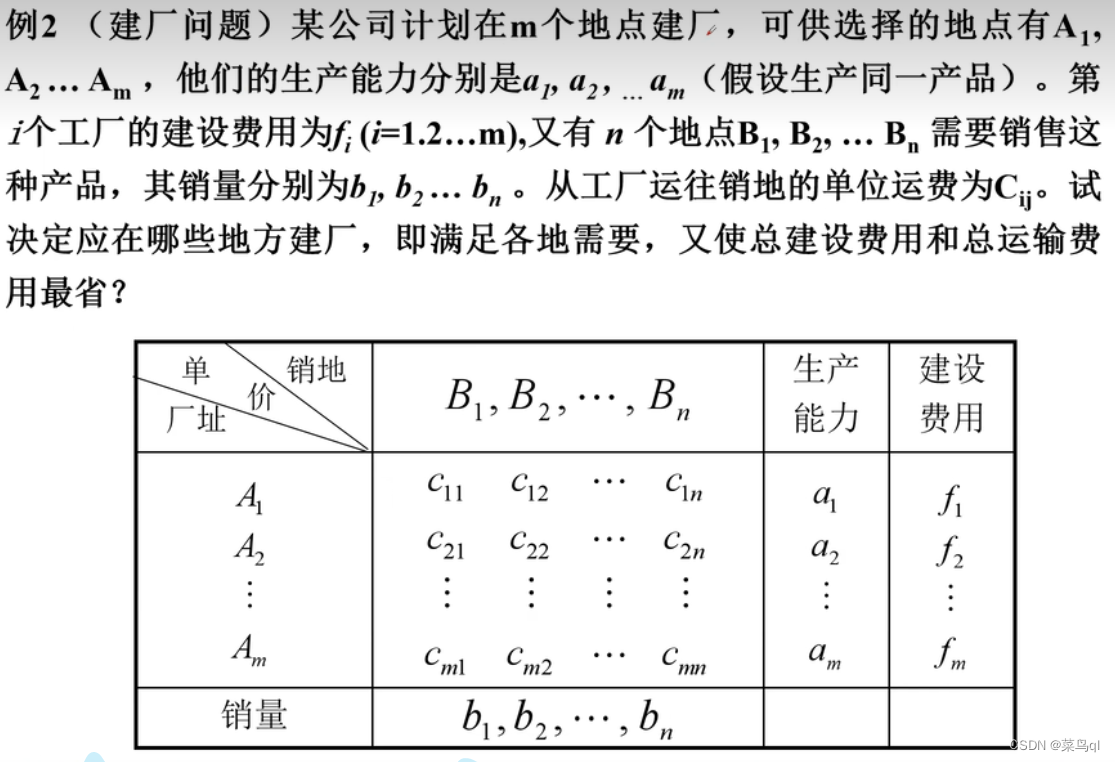
解：

 

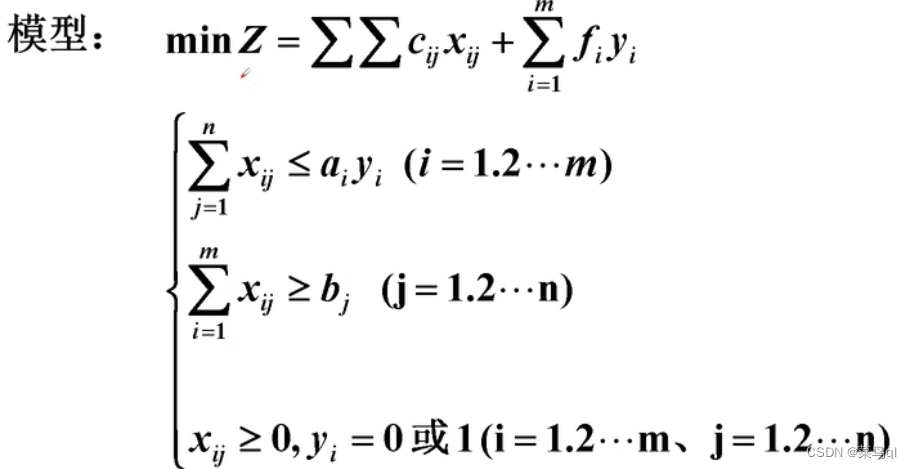
 解释：
等式：Z即为总运输费用+总建设费用
不等式一：工厂运出量<=工厂生产量
不等式二：运地接受到的运量>=此地销量（条件“满足各地需要”）

五 整数规划数学模型

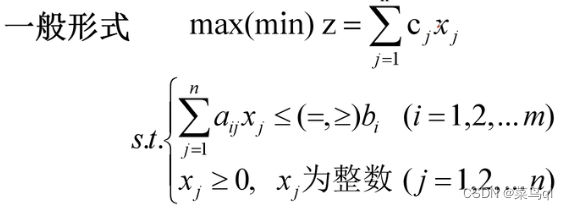
 依照决策变量取整要求不同，整数规划可分为

 解释：

松弛变量：如要满足x1+x2<=10,可设x1+x2+x3=10，当x3>=0时，满足x1+x2<=10。此时称x3为松弛变量，主要解决将<=问题转化为=问题。

剩余变量：如要满足x1+x2>=10,可设x1+x2-x3=10，当x3>=0时，满足x1+x2>=10。此时称-x3为剩余变量。

六 整数线性规划与线性规划的关系

一些简单的推论：

 ILP：整数线性规划

七 整数线性规划的求解方法

例：

 

 

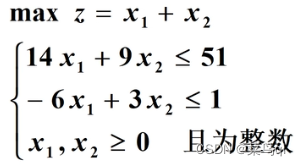
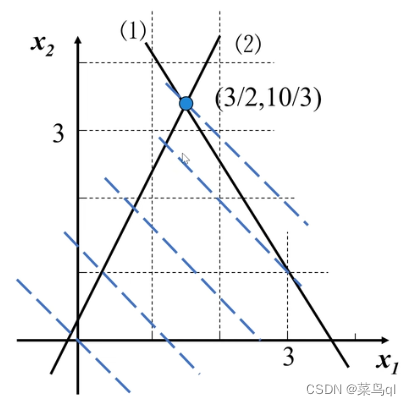
当目标范围较小时，可用完全枚举法：按整数规划约束条件，其可行解肯定在线性规划问题的可行域内且为整数点。故整数规划问题的可行解是一个有限集。因此，可将集合内的整数点一一找出，其最大目标函数的值为最优解。

当目标范围较大时，常用的求解整数规划的方法有：分支定界法和割平面法。

对于特别的0-1规划问题（指派问题），采用隐枚举法和匈牙利法。

1.分支定界法

 注：
松弛问题：即线性规划问题
ILP：整数线性规划问题

如：求出x=2.3，则可设xi<=2;xi>=3

待补充