根据财政收入数据进行预测

分析财政收入预测背景

财政收入，是指政府为履行其职能、实施公共政策和提供公共物品与服务需要而筹集的一切资金的总和。财政收入表现为政府部门在一定时期内(一般为一个财政年度)所取得的货币收入。财政收入是衡量一国政府财力的重要特征，政府在社会经济活动中提供公共物品和服务的范围和数量，在很大程度上取决于财政收入的充裕状况。
在我国现行的分税制财政管理体制下，地方财政收入不但是国家财政收入的重要组成部分，而且具有其相对独立的构成内容。如何制定地方财政支出计划，合理分配地方财政收入，促进地方的发展，提高市民的收入和生活质量是每个地方政府需要考虑的首要问题。因此，地方财政收入预测是非常必要的。

一、灰色预测模型以及SVR预测模型

任务描述

基于灰色预测对小样本数据集的优良性能，首先对单个特征建立灰色预测模型，得到各特征2014年和2015年的预测值。然后对2013年以前的训练数据集建立支持向量回归模型，将建立好的模型与灰色预测模型相结合，对2014年和2015年的财政收入进行预测。

任务分析

(1）加载GM(1,1)源文件，构建灰色预测模型，得到各特征值。
(2）使用LinearSVR函数，构建支持向量回归模型，得到2014年及2015年财政收入预测值。

任务流程

（1）构建灰色预测模型，获取预测特征值

建立了一个自定义灰色预测函数GM11

# -*- coding: utf-8 -*-
"""
Created on Mon Mar 28 11:12:48 2022

@author: 13549
"""

def GM11(x0): #自定义灰色预测函数
  import numpy as np
  x1 = x0.cumsum() #1-AGO序列
  z1 = (x1[:len(x1)-1] + x1[1:])/2.0 #紧邻均值（MEAN）生成序列
  z1 = z1.reshape((len(z1),1))
  B = np.append(-z1, np.ones_like(z1), axis = 1)
  Yn = x0[1:].reshape((len(x0)-1, 1))
  [[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数
  f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2)) #还原值
  delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)]))
  C = delta.std()/x0.std()
  P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
  return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率

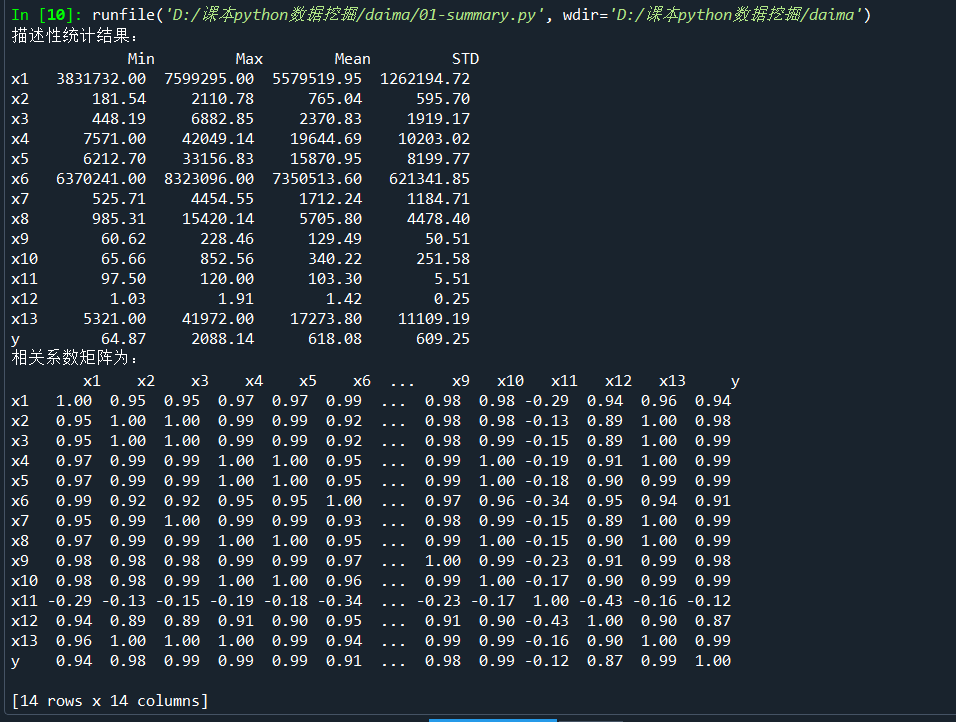
（2）描述性统计分析，得到特征之间的相关性关系

# 代码6-1

import numpy as np
import pandas as pd

inputfile = '../data/data.csv' # 输入的数据文件
data = pd.read_csv(inputfile) # 读取数据

# 描述性统计分析
description = [data.min(), data.max(), data.mean(), data.std()]  # 依次计算最小值、最大值、均值、标准差
description = pd.DataFrame(description, index = ['Min', 'Max', 'Mean', 'STD']).T  # 将结果存入数据框
print('描述性统计结果：\n',np.round(description, 2))  # 保留两位小数



# 代码6-2

# 相关性分析
corr = data.corr(method = 'pearson')  # 计算相关系数矩阵
print('相关系数矩阵为：\n',np.round(corr, 2))  # 保留两位小数

绘制热力图

# 绘制热力图
import matplotlib.pyplot as plt
import seaborn as sns
plt.subplots(figsize=(10, 10)) # 设置画面大小 
sns.heatmap(corr, annot=True, vmax=1, square=True, cmap="Blues") 
plt.title('相关性热力图')
plt.show()
plt.close

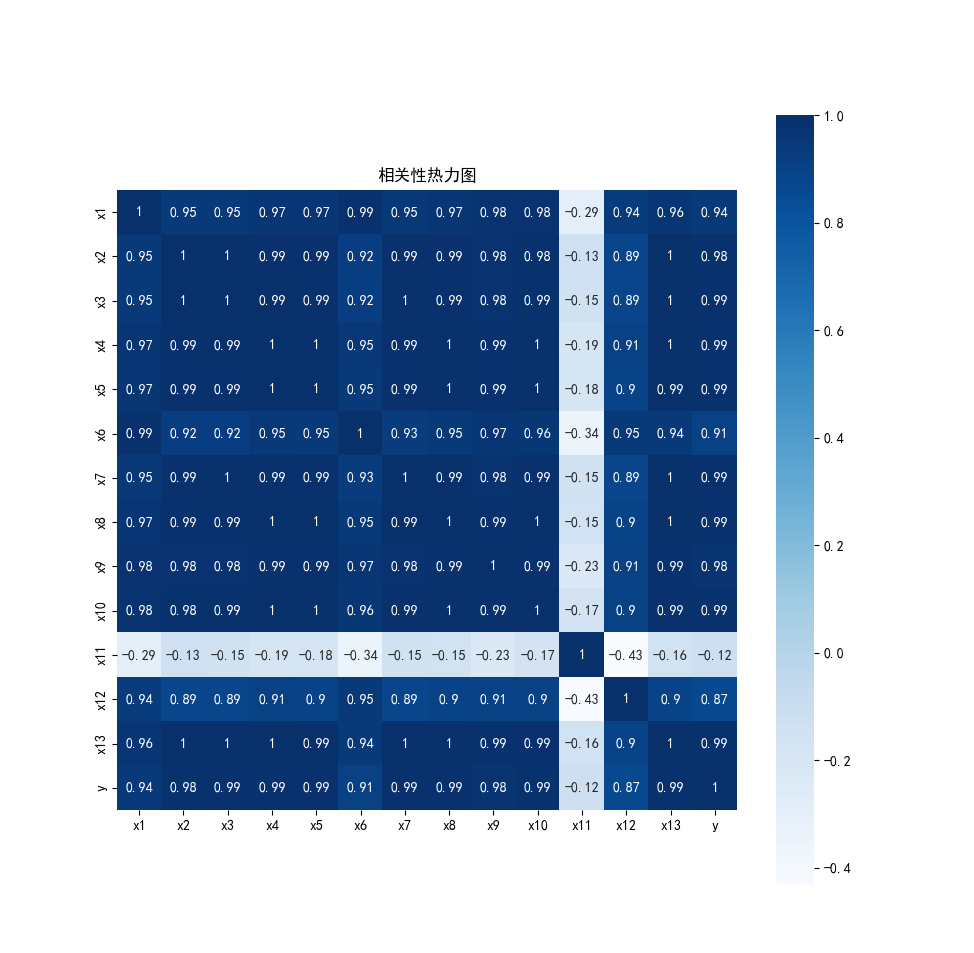
由热力图可知，选取的各特征除了x11外，其他特征与y的相关性很强，可以用作财政收入预测分析的关键特征，但这些特征之间存在信息的重复，需要对特征进行进一步筛选。

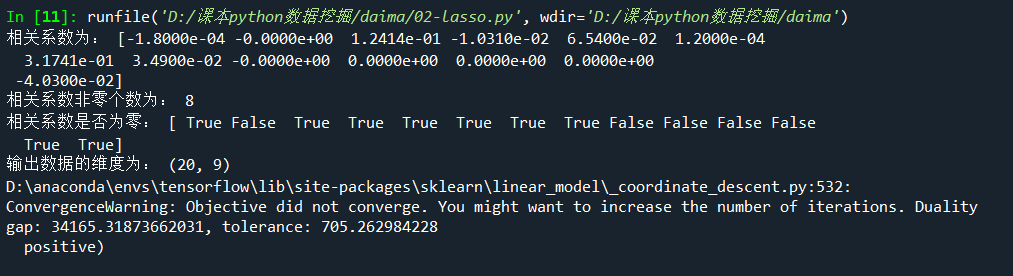
（3）使用Lasso回归方法进行关键特征选取

#-*- coding: utf-8 -*-

# 代码6-4

import numpy as np
import pandas as pd
from sklearn.linear_model import Lasso

inputfile = 'D:/课本python数据挖掘/data/data.csv'  # 输入的数据文件
data = pd.read_csv(inputfile)  # 读取数据
lasso = Lasso(1000)  # 调用Lasso()函数，设置λ的值为1000
lasso.fit(data.iloc[:,0:13],data['y'])
print('相关系数为：',np.round(lasso.coef_,5))  # 输出结果，保留五位小数

print('相关系数非零个数为：',np.sum(lasso.coef_ != 0))  # 计算相关系数非零的个数


mask = lasso.coef_ != 0  # 返回一个相关系数是否为零的布尔数组
mask = np.append(mask,True)
print('相关系数是否为零：',mask)

outputfile ='D:/课本python数据挖掘/output/new_reg_data.csv'  # 输出的数据文件
new_reg_data = data.iloc[:, mask]  # 返回相关系数非零的数据
new_reg_data.to_csv(outputfile)  # 存储数据
print('输出数据的维度为：',new_reg_data.shape)  # 查看输出数据的维度

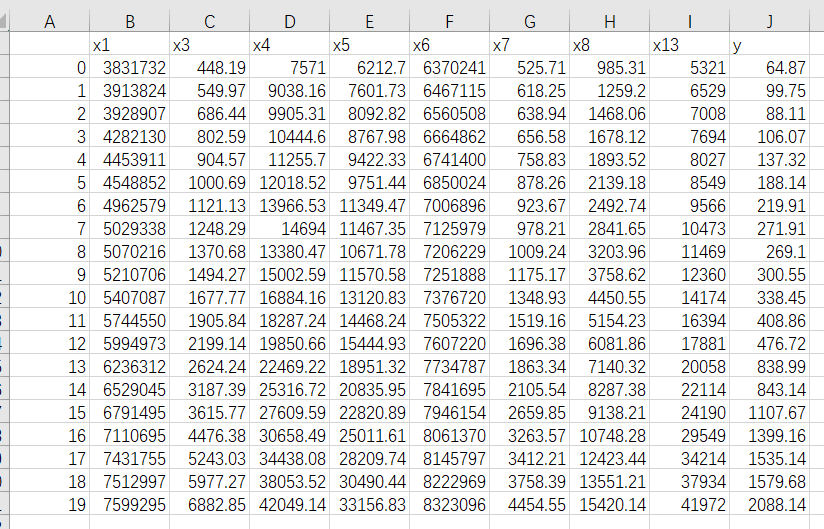
 并得到关键因素的数据（文件名为new_reg_data.csv）：

（4）构建灰色预测模型，并预测2014年和2015年的财政收入

#-*- coding: utf-8 -*-

# 代码6-5

import sys
sys.path.append('../code')  # 设置路径
import numpy as np
import pandas as pd
from GM11 import GM11  # 引入自编的灰色预测函数

inputfile1 = 'D:/课本python数据挖掘/output/new_reg_data.csv'  # 输入的数据文件
inputfile2 = 'D:/课本python数据挖掘/data/data.csv'  # 输入的数据文件
new_reg_data = pd.read_csv(inputfile1)  # 读取经过特征选择后的数据
data = pd.read_csv(inputfile2)  # 读取总的数据
new_reg_data.index = range(1994, 2014)
new_reg_data.loc[2014] = None
new_reg_data.loc[2015] = None
l = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
for i in l:
  #f=GM11(new_reg_data.loc[range(1994,2014),i].as_matrix())[0]
  f = GM11(new_reg_data.loc[range(1994, 2014),i].values)[0]
  new_reg_data.loc[2014,i] = f(len(new_reg_data)-1)  # 2014年预测结果
  new_reg_data.loc[2015,i] = f(len(new_reg_data))  # 2015年预测结果
  new_reg_data[i] = new_reg_data[i].round(2)  # 保留两位小数
outputfile = 'D:/课本python数据挖掘/output/new_reg_data_GM11.xls'  # 灰色预测后保存的路径
y = list(data['y'].values)  # 提取财政收入列，合并至新数据框中
y.extend([np.nan,np.nan])
new_reg_data['y'] = y
new_reg_data.to_excel(outputfile)  # 结果输出
print('预测结果为：\n',new_reg_data.loc[2014:2015,:])  # 预测结果展示

（5）构建支持向量回归模型,得到2014年及2015年财政收入预测值

预测之前，需要将数据进行标准化处理，那么就用到了z-score标准化。z-score标准化能消除数据量纲上的影响，减少迭代次数。

data_train = data.loc[range(1994,2014)].copy()  # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std  # 数据标准化

利用svr模型得到2014年和2015年的财政收入预测值

# -*- coding: utf-8 -*-
"""
Created on Mon Mar 28 11:17:48 2022

@author: 13549
"""
# 代码6-6

import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
import pandas as pd

inputfile = 'D:/课本python数据挖掘/output/new_reg_data_GM11.xls'  # 灰色预测后保存的路径
data = pd.read_excel(inputfile)  # 读取数据
data.index = range(1994,2016)
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']  # 属性所在列
#data_train = data.loc[range(1994,2014)].copy()  # 取2014年前的数据建模
data_train = data.loc[range(1994,2014)].copy()  # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean)/data_std  # 数据标准化
x_train = data_train[feature].values  # 属性数据
y_train = data_train['y'].values  # 标签数据

linearsvr = LinearSVR()  # 调用LinearSVR()函数
linearsvr.fit(x_train,y_train)
x = ((data[feature] - data_mean[feature])/data_std[feature]).values  # 预测，并还原结果。
data['y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']
outputfile = 'D:/课本python数据挖掘/output/new_reg_data_GM11_revenue.xls'  # SVR预测后保存的结果
data.to_excel(outputfile)

print('真实值与预测值分别为：\n',data[['y','y_pred']])

fig = data[['y','y_pred']].plot(subplots = True, style=['b-o','r-*'])  # 画出预测结果图
plt.show()

 

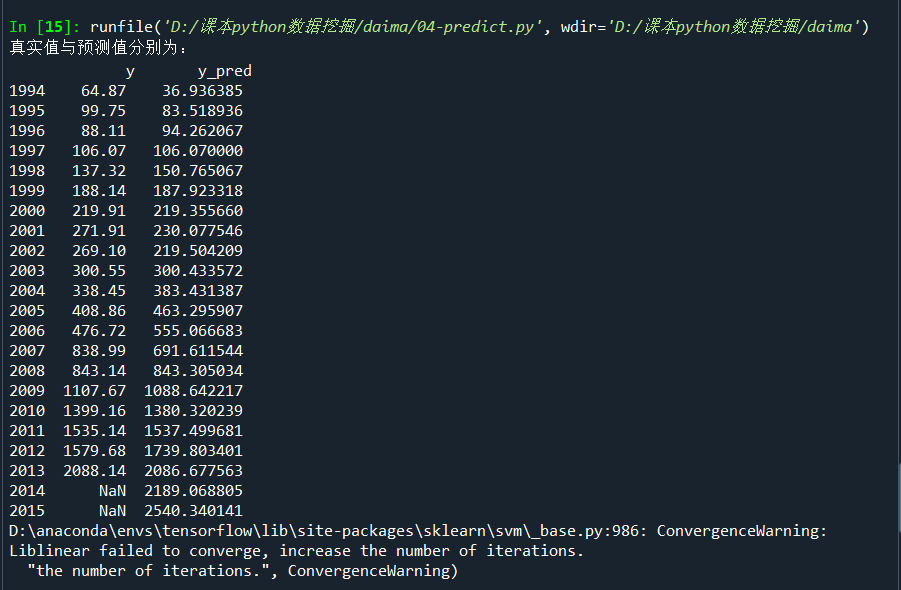
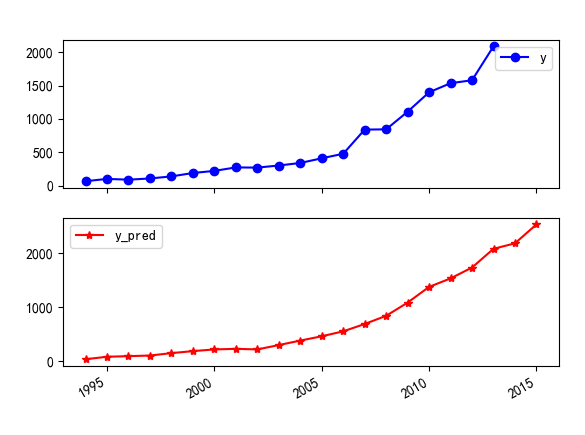
根据实际值与预测值以及预测效果图的对比，建立的支持向量回归模型拟合效果优良，可以用于预测财政收入。

其中2014年和2015年的财政收入预测值分别为

 

二、ARIMA模型

任务描述

将2013年以前的训练数据按其先后发生的时间顺序排列而成，使用时序图、自相关图、平稳性进行检验序列是否平稳，如果该序列是非平稳的，还需要再对序列进行差分处理，最后根据这些历史数据对2014年和2015年的财政收入进行预测。

任务分析

(1）使用时序图、自相关图、平稳性检验序列是否平稳。
(2）如果该序列是非平稳的，还需要再对序列进行差分处理。

任务流程

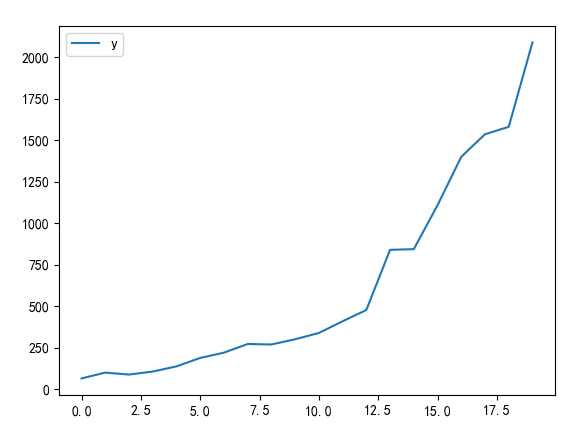
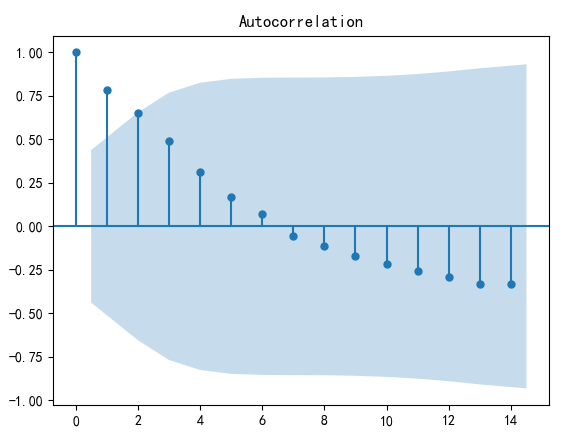
（1）使用时序图、自相关图、平稳性检验序列是否平稳

import pandas as pd
# 参数初始化
discfile = '../data/data.csv'
forecastnum = 2

# 读取数据，指定日期列为指标，pandas自动将“日期”列识别为Datetime格式
data = pd.read_csv(discfile)

x = 'y'
data = data[[x]]

# 时序图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
data.plot()
plt.show()

# 自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()

# 平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print('原始序列的ADF检验结果为：', ADF(data['y']))
# 返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore

时序图

自相关图

 平稳性检测

 (2）该序列是非平稳的，对序列进行差分处理

# 差分后的结果
D_data = data.diff().dropna()
D_data.columns = ['收入差分']
D_data.plot()  # 时序图
plt.show()
plot_acf(D_data).show()  # 自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data,lags = 8).show()  # 偏自相关图
print('差分序列的ADF检验结果为：', ADF(D_data['收入差分']))  # 平稳性检测

# 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print('差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1))  # 返回统计量和p值

from statsmodels.tsa.arima_model import ARIMA

差分后的时序图

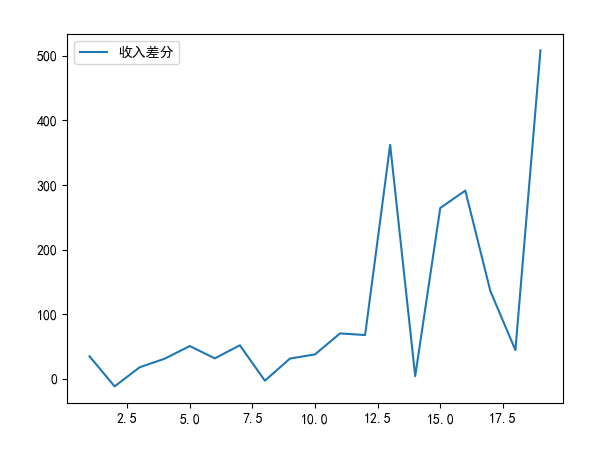
 差分后的自相关图

 

 

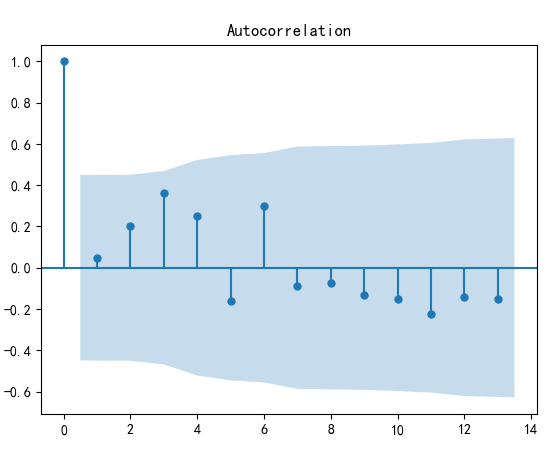
差分后的偏自相关图

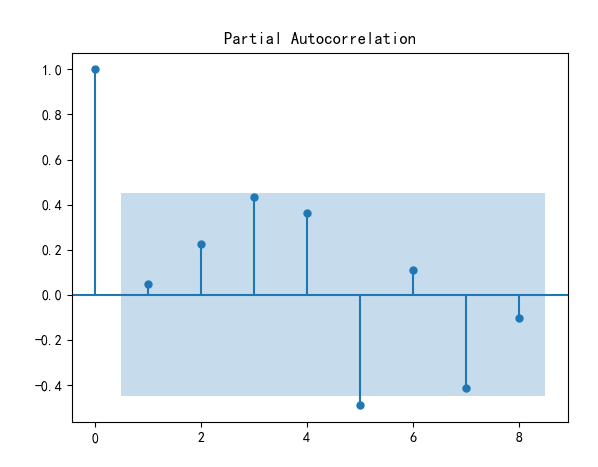
 差分后的平稳性检验和白噪声检验

 （3）定阶

# 定阶
data['y'] = data['y'].astype(float) 
pmax = int(len(D_data)/10)  # 一般阶数不超过length/10
qmax = int(len(D_data)/10)  # 一般阶数不超过length/10
bic_matrix = []  # BIC矩阵
for p in range(pmax+1):
  tmp = []
  for q in range(qmax+1):
    try:  # 存在部分报错，所以用try来跳过报错。
      tmp.append(ARIMA(data, (p,1,q)).fit().bic)
    except:
      tmp.append(None)
  bic_matrix.append(tmp)

bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值

p,q = bic_matrix.stack().idxmin()  # 先用stack展平，然后用idxmin找出最小值位置。
print('BIC最小的p值和q值为：%s、%s' %(p,q)) 
model = ARIMA(data, (p,1,q)).fit()  # 建立ARIMA(0, 1, 1)模型
print('模型报告为：\n', model.summary2())
print('预测未来2年，其预测结果、标准误差、置信区间如下：\n', model.forecast(2))

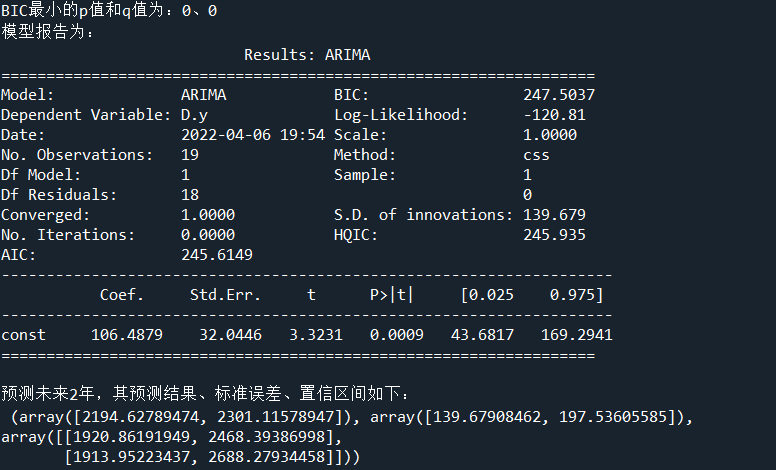
其中未来两年的财政收入预测值分别为

 

 

 三、结论

灰色预测算法+SVR算法预测的模型效果更好