数据结构、算法及线性表总结
数据结构、算法及线性表总结：
一. 思维导图
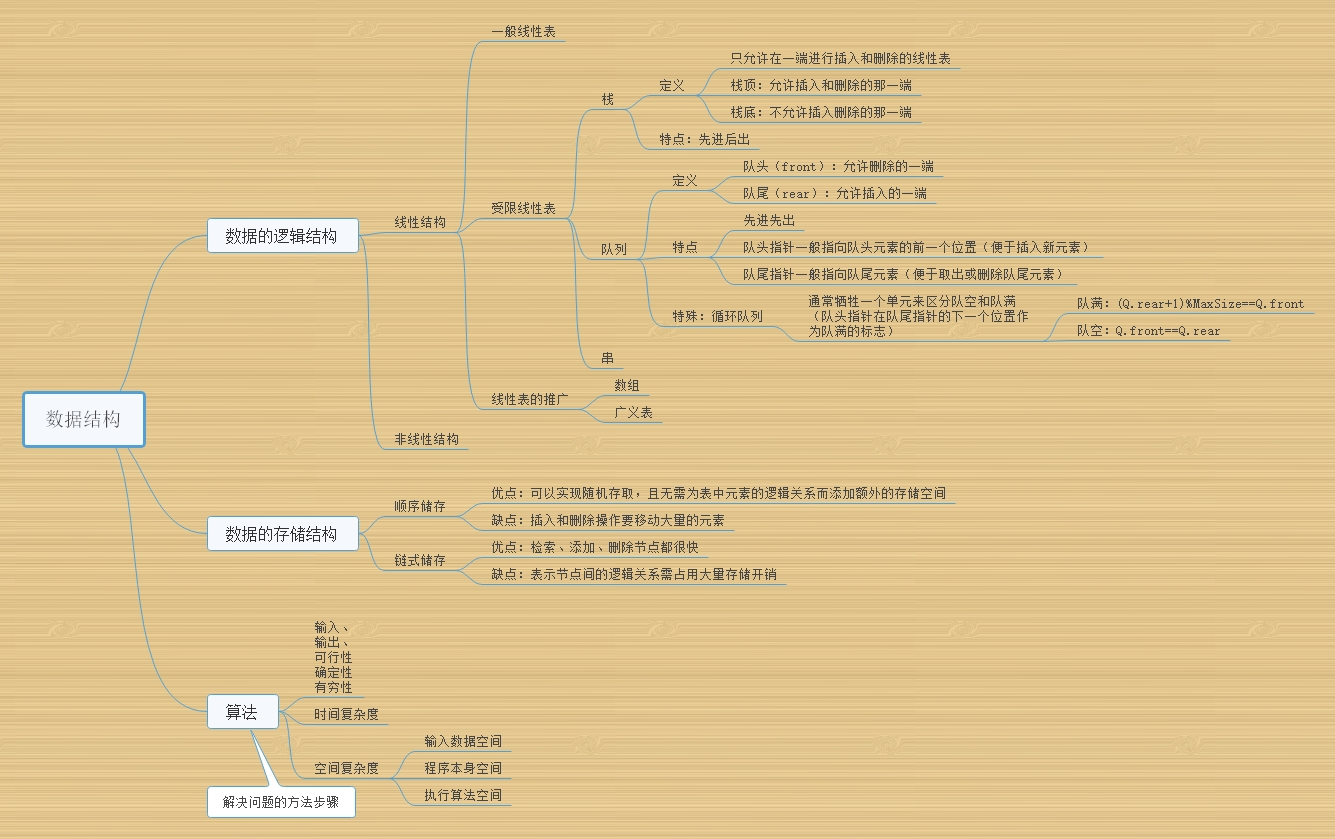
二. 重要概念笔记
1.数据结构相关术语：
数据元素：组成数据、有一定意义的基本单位，在计算机中被当做整体来处理。
数据项：数据结构中不可分割的最小单位。
数据对象：性质相同的数据元素的集合，是数据的子集，性质相同，也就是说数据元素的数据项相同（具有相同的数量和类型的数据项）。
数据结构：相互之间存在的一种或多种特定关系的数据元素的集合。
2.物理结构
物理结构是指数据的逻辑结构在计算机中的存储形式，物理结构有以下两种：
顺序存储结构：把数据元素存放在地址连续的存储单元中，数据间的逻辑关系和物理关系是一致的。
链式存储结构：在计算机中把数据元素存放在任意的存储单元中，可以是连续的，也可以是不连续的，用指针将每个数据元素联系起来。
3.算法：
特性：有穷性、确定性、可行性、输入、输出。
评判算法优劣：
时间复杂度( T(n)=O( f(n) ) ,n为问题规模)与
空间复杂度(占用的额外储存空间随问题规模的变化)
4.常见的时间复杂度耗时排列：
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(!n)<O(nn)
(时间复杂度通常是指最坏情况的耗时时间)
5.线性表：
零个或多个数据元素的有限序列
线性表的两种存储结构：顺序存储&链式存储。
操作方法：头插法，尾插法。
6.栈：
是限定仅在表尾进行插入和删除操作的线性表，先进后出。
队列：是只允许在一端插入数据在另一端删除数据的线性表，先进先出。
7.串：
零个或多个字符组成的有限序列，又叫字符串。
模式匹配算法：BF算法、KMP算法。
8.地址计算：
若求矩阵A[M][N]中i行j列元素的地址，则
行优先：首地址+(iM+j)k
列优先：首地址+(iN+j)k
(K为单个元素所占的储存空间)
三. 疑难问题及解决方案
pta题目：求前缀表达式的值。
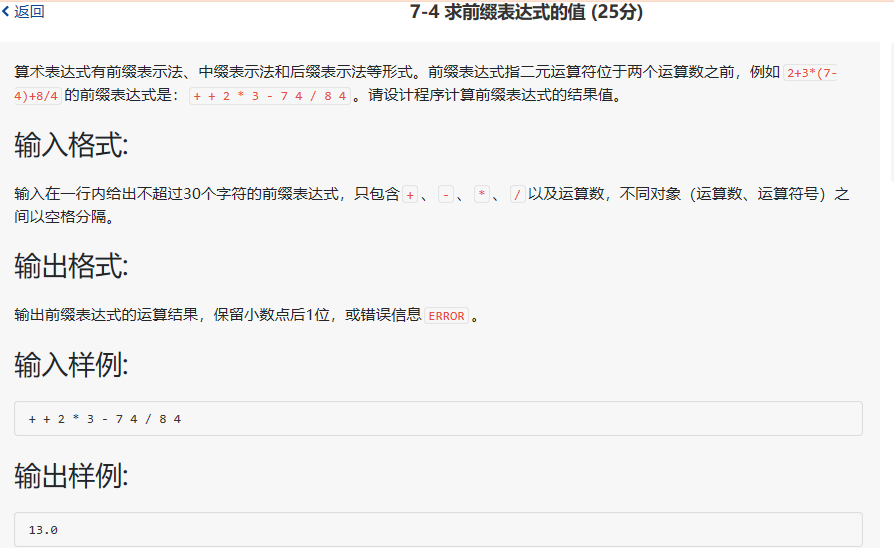
思路：
仔细审题，发现题目并没有说输入数据一定是正整数，所以负数和小数的情况也要考虑到。
由于是前缀表达式，所以必然是先有运算符，再有两个数字的，因此我们从后往前遍历。
对于上面说的小数与负数的特殊情况，当输入小数时，“.”前后是没有空格的，我们读取从右至左，所以会先读到“.”前的部分，然后是“.”,最后是“.”后的部分，因此只需要让“.”后的每一位除以十再加上前一位，如此这样直到遇到小数点为止，再将算出来的数加上小数点前的部分就行了。
当遇到负数时，因为“-”和数字中间一定没有空格，有空格一定是减号，所以遍历时如果遇到数字和“-”挨着，那么就一定是负数。
排除特殊情况后，每读取出一个数就压入栈中，当读到运算符时，就将栈顶的两个元素取出st.top()并删除这两个元素st.pop()，然后计算值并将值压入栈中以便下次计算st.push(sum)。
完整代码如下：
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <string>
#include <cctype>
using namespace std;
stack <double> st;
int main()
{
string s;
getline(cin, s);
for (int i = s.size() - 1; i >= 0; i--)
{
if (isdigit(s[i]))
{
double mul = 10, num = s[i] - '0';
for (i--; i >= 0; i--)
{
if (isdigit(s[i])) //检验参数是否为数字字符
{
num += (s[i] - '0') * mul; //将数字字符转化为数字
mul *= 10;
}
else if (s[i] == '.') //逐位处理小数点后的数据
{
num /= mul;
mul = 1;
}
else if (s[i] == '-') //处理负数
num = -num;
else
break;
}
st.push(num);
}
else if (s[i] != ' ')
{
double a, b, sum;
a = st.top(); //提出栈内数据
st.pop();
b = st.top();
st.pop();
switch (s[i])
{
case '+':
sum = a + b;
break;
case '-':
sum = a - b;
break;
case '*':
sum = a * b;
break;
case '/':
{
if (b == 0)
{
cout << "ERROR";
return 0;
}
sum = a / b;
}
}
st.push(sum); //计算一次结果并压入栈中
}
}
printf("%.1lf", st.top());
}
