HDU - 6760 Math is Simple （差分，莫比乌斯函数）

HDU - 6760 Math is Simple （差分，莫比乌斯函数）

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=6760

Problem Description

Here is a simple math. You are given an integer n. Your task is to calculate the following:

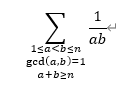
思路：

\[F(n)=\sum_{1\le a< b\leq n\\gcd(a,b)=1\\ a+b\ge n}{\frac{1}{ab}} \]

我们尝试递推求\(F(n)\)，

思考发现，从\(F(n-1)\)转移到\(F(n)\)需要曾增加 \(a+b=n\)的方案，减去\(a+b=n-1\)的方案。

即：

\[F(n)=F(n-1)+\sum_{1\le a< b\leq n\\gcd(a,b)=1\\ a+b=n}{\frac{1}{ab}}-\sum_{1\le a< b\leq n-1\\gcd(a,b)=1\\ a+b=n-1}{\frac{1}{ab}} \]

注意：上式中\(1\le a< b\leq n,1\le a< b\leq n-1\)，

其实意义上严格的写法应该是\(1\le a< b< n\)，但因为\(b=n\)时，\(\mathit a\)无取值，所以是等价的。

观察到右式中只有\(n,n-1\)之差，所以我们可以设：

\[g(n)=\sum_{1\le a< b\leq n\\gcd(a,b)=1\\ a+b=n}{\frac{1}{ab}} \]

又因为：

\[\frac{1}{ab}=\frac{1}{a(n-a)}=\frac{1}{n}(\frac{1}{a}+\frac{1}{n-a})=\frac{1}{n}(\frac{1}{a}+\frac{1}{b}) \\ \\ gcd(a,b)=gcd(a,a+b)=gcd(a,n) \]

所以：

\[g(n)=\sum_{1\le a \le n \\gcd(a,n)=1}{\frac{1}{a}} \]

所以：

\[F(n)=F(n-1)+g(n)-g(n-1) \\ F(n-1)=F(n-2)+g(n-1)-g(n-2) \\ F(n-2)=F(n-3)+g(n-2)-g(n-3) \\ \dots \]

所以：

\[F(n)=g(n)+F(2)-g(2) \]

加入可得：

\[F(2)=\frac{1}{2}\\ g(2)=0 \\ F(n)=\frac{1}{n}*g(n)+\frac{1}{2} \]

因此问题转化为求\(g(n)\)

\[g(n)=\sum_{1\le a \le n \\gcd(a,n)=1}{\frac{1}{a}} \\ =\sum_{1\le a \le n}{\frac{1}{a}[gcd(a,n)=1]} \]

莫比乌斯函数有性质：

\[\sum_{d|n}{\mu(d)}=\begin{cases} 1,&\ n=1 \\ 0,& \ n>1 \end{cases} \\\ So: [gcd(a,n)=1]=\sum_{d|gcd(a,n)}{\mu(d)} \]

\[∴ g(n)=\sum_{1\le a \le n}\frac{1}{a}\ {\sum_{d|gcd(a,n)}{\mu(d)}} \]

我们将\(g(n)\)改写为枚举\(\mathit d\) 的形式，

因为：d是n的因子，又是a的因子 。a是\([1,n]\)中d的倍数，即： \(\frac{1}{a}=\frac{1}{d*i}\)

\[∴g(n)=\sum_{d|n}\mu(d)\sum_{i=1}^{n/d}{\frac{1}{id}} \]

将右侧的\(\mathit d\) 提出来，

\[g(n)=\sum_{d|n}{\mu(d)\frac{1}{d} \sum_{i=1}^{n/d}{\frac{1}{i}}} \\ Def：S(x)=\sum_{i=1}^{x}{\frac{1}{x}} \\∴ g(n)=\sum_{d|n}{\mu(d)\frac{1}{d}S(n/d)} \]

而\(S(x)\)我们可以通过\(O(n)\)预处理出来，

又因为内存限制，开\(1e8\) 大小的int数组，大概消耗$ 350Mb$，所以只能开一个\(1e8\)的数组，

\(\mu(n)\)我们就只能\(O(\sqrt{n}+2^{pd(n)})\)时间复杂度求解，

其中\(pd(n)\)是n的素因子种类数，在\(n\leq 10^8\)，\(pd(n)\leq 8\)。即前8个质数相乘大于\(1e8\)。

因为一个数\(\mathit x\)的某个质因子次幂大于1时，\(\mu(x)=0\)，所以我们只需要\(O(\sqrt n)\)得到\(\mathit n\) 的所有质因子，然后\(O(2^{pd(n)})\)二进制枚举所有\(\mu(d)\not=0\)的\(\mathit d\) 即可，即一个因子取或不取。

所以本题的时间复杂度为：

\(O(10^8+T*(\sqrt{n}+2^{pd(n)}))\) 大概在\(2e8\)范围内，可以接受。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <bits/stdc++.h>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define chu(x)  if(DEBUG_Switch) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) { if (a == 0ll) {return 0ll;} a %= MOD; ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
ll poww(ll a, ll b) { if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a ;} a = a * a ; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
inline long long readll() {long long tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
inline int readint() {int tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') fh = -1; c = getchar();} while (c >= '0' && c <= '9') tmp = tmp * 10 + c - 48, c = getchar(); return tmp * fh;}
void pvarr_int(int *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%d%c", arr[i], i == n ? '\n' : ' ');}}
void pvarr_LL(ll *arr, int n, int strat = 1) {if (strat == 0) {n--;} repd(i, strat, n) {printf("%lld%c", arr[i], i == n ? '\n' : ' ');}}
const int maxn = 100000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
#define DEBUG_Switch 0
const int mod = 998244353;
int inv[maxn];
// inv[i]= (1/i) % mod
int ans;
int p[30];
int cnt;
int n;
void dfs(int pos, int now, int u)
{
	if (pos > cnt)
	{
		ans = (ans + 1ll * u *  ((inv[now] - inv[now - 1] + mod) % mod) % mod * inv[n / now ] % mod) % mod;
		return ;
	}
	dfs(pos + 1, now, u);
	dfs(pos + 1, now * p[pos], mod - u);
}
int main()
{
#if DEBUG_Switch
	freopen("C:\\code\\input.txt", "r", stdin);
	freopen("C:\\code\\output.txt", "w", stdout);
#endif
	inv[1] = 1;
	for (int i = 2; i < maxn; i++)
		inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;
	for (int i = 2; i < maxn; i++)
		inv[i] = ( inv[i] + inv[i - 1]) % mod;
	int t;
	t = readint();
	while (t--)
	{
		ans = 0ll; cnt = 0;
		n = readint();
		if (n <= 2)
		{
			printf("%d\n", (inv[2] - 1 + mod) % mod);
			continue;
		}
		int temp = n;
		for (int i = 2; i * i <= temp; ++i)
		{
			if (temp % i == 0)
			{
				p[++cnt] = i;
				while (temp % i == 0)
					temp /= i;
			}
		}
		if (temp > 1)
			p[++cnt] = temp;
		dfs(1, 1, 1);
		ans = (1ll * ans *  ((inv[n] - inv[n - 1] + mod) % mod)) % mod;
		ans = (ans +  ((inv[2] - 1 + mod) % mod)) % mod;
		printf("%d\n", ans );
	}
	return 0;
}