平面n边形组成封闭立体几何图形，所需的最小n边形数量

Do you have good taste in something like fine art? ————qianxin

平面n边形组成封闭立体几何图形，所需的最小n边形数量

前言

‘Find a ...’ or ‘Find all ...’ questions, which requires one to find something (or everything) that satisfies certain requirements;
首先，修改问题为：平面x边形组成封闭y面体，所需的最小x边形数量

Objective

• \(y\)面体
• \(x\)边形

Notation

• \(x\)表示多边形边数，
• \(y\)表示\(y\)面体，
• \(z\)表示\(y\)面体顶点个数。
• \(a\)表示每点平均共享边条数。

Equation

• 自然约束：\(x\)边形组成\(y\)面体有\(\frac{xy}{2}\)条边，\(z\)个点，\(x \ge 3,y \ge 4,z \ge 4\)
• \(y\)面体每点平均被\(a\)条边共享，即\(z=\frac{xy}{a}\),\(a \ge 3\)
• 欧拉公式：\(z+y-\frac{xy}{2}=2\)

目标：确定x的取值范围

通过欧拉公式加自然约束和\(y\)面体每点平均被\(a\)条边共享，可得\(y(1-\frac{a-2}{2a}x)=2\)。
可见，当\(\frac{a-2}{2a}x \ge \frac{3(a-2)}{2a} \ge 1\)时，欧拉方程不成立，即\(a \ge 6时方程不成立。\)

若问题为平面6边形可以组成y面体，可用反证法

若存在只由6边形组成立体图形，由欧拉公式有\(2x+x-3x=2\)，不成立

结论

平面\(x\)边形组成\(y\)面体，所需的最小\(x\)边形数量为\(3，4，5\)。

注意

立体图形有洞的话，\(V+F-E=2-2g\)，即亏格为\(1\)，且每个面都是六边形的立体图形是被允许的。
如这个https://www.wikiwand.com/en/Szilassi_polyhedron。有洞的流形一直是特殊的。
这个公式也解释了为什么三角学是初等数学很重要的一个部分。

Euler's polyhedron formula(\(V-E+F = \chi\))

Euler's formula states that if a finite, connected, planar graph is drawn in the plane without any edge intersections, and v is the number of vertices, e is the number of edges and f is the number of faces (regions bounded by edges, including the outer, infinitely large region), then

\[V-E+F=2 \]

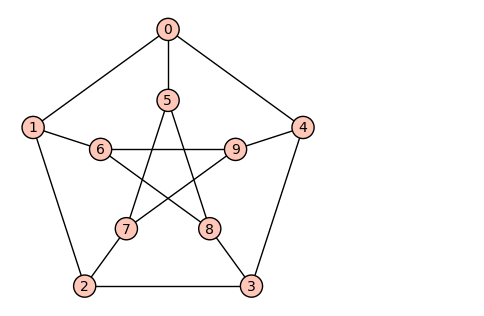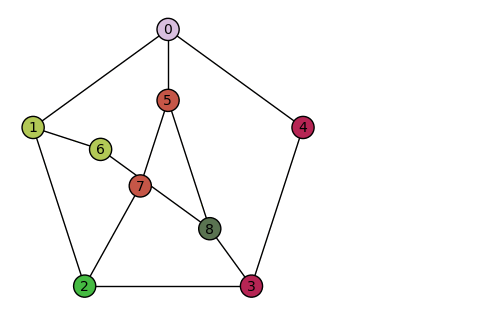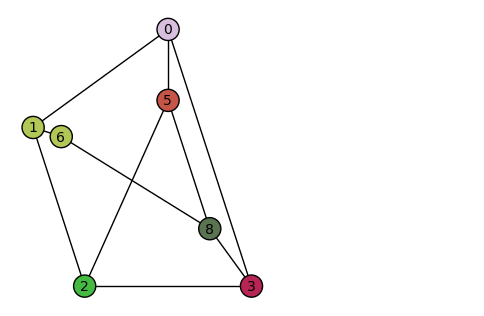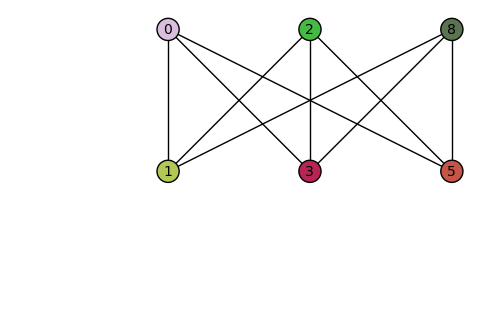
An animation showing that the Petersen graph contains a minor isomorphic to the K3,3 graph, and is therefore non-planar

ChangeLog

2022/1/18 21:26 公元1758年，Euler给出了Euler's polyhedron formula，并提出了一系列相关的Euler characteristic \(\chi\) ，\(\chi = V-E+F\)。