常见动态规划题 原理及Java实现

动态规划的求解过程：

(1) 划分子问题：将原问题划分为若干子问题，每个子问题对应一个决策阶段，并子问题之间有重叠关系。
(2) 确定动态规划函数：根据子问题之间重叠关系找到子问题满足的递推关系式。
(3) 填写表格：以自底向上的方式计算各个子问题的解并填表，实现动态规划。

上述过程可求出问题的最优值，但要求出具体的最优解，通常还需要在动态规划过程中记录必要信息，再根据最优决策序列构造最优解。

eg.1
数塔问题

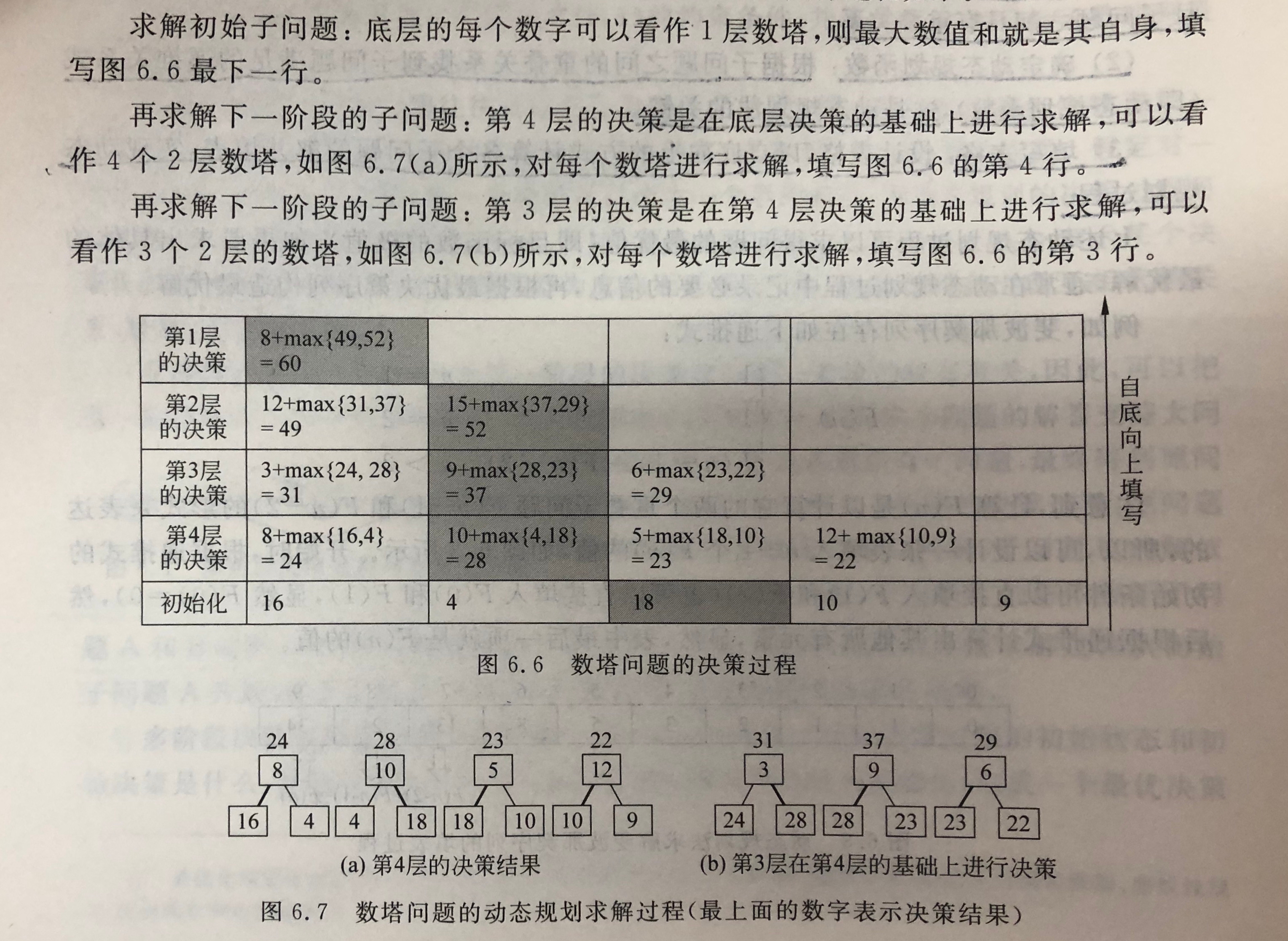
动态规划函数：

maxAdd[n-1][j] = d[n-1][j] (0<=j<=n-1)
maxAdd[i][j] = d[i][j] +max{maxAdd[i+1][j],maxAdd[i+1][j+1]}
( 0<=i<=n-2, 0<=j<=i )

伪代码：

java实现

package DynamicProgramming;

public class DataTower {
	static int Dt(int[][] d,int n) {
		int[][] maxAdd = new int[n][n];
		int[][] path = new int[n][n];
		int i,j;
		for(j=0;j<n;j++) {
			//初始化底层决策结果
			maxAdd[n-1][j] = d[n-1][j];
		}
		for(i=n-2;i>=0;i--) { //进行第i层决策
			for(j=0;j<=i;j++) { //填写maxAdd[i][j],只填写下三角
				if(maxAdd[i+1][j]>maxAdd[i+1][j+1]) {
					maxAdd[i][j] = d[i][j] + maxAdd[i+1][j];
					path[i][j] = j;
				}
				else {
					maxAdd[i][j] = d[i][j] + maxAdd[i+1][j+1];
					path[i][j] = j+1;
				}
			}
		}
		System.out.println("path:"+d[0][0]);
		j = path[0][0];
		for(i=1;i<n;i++) {
			System.out.println(d[i][j]);
			j = path[i][j];
		}
		return maxAdd[0][0];
	}
	public static void main(String[] args) {
		int[][] d = new int[][] {{8,0,0,0,0},
								{12,15,0,0,0},
								{3,9,6,0,0},
								{8,10,5,12,0},
								{16,4,18,10,9}};
		System.out.println(Dt(d,5));
		
	}
}