LeetCode198 打家劫舍（动态规划

作者：nettee
链接：https://leetcode-cn.com/problems/house-robber/solution/dong-tai-gui-hua-jie-ti-si-bu-zou-xiang-jie-cjavap/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

动态规划的的四个解题步骤是：

• 定义子问题
• 写出子问题的递推关系
• 确定 DP 数组的计算顺序
• 空间优化（可选）

步骤一：定义子问题

什么是子问题？子问题是和原问题相似，但规模较小的问题。
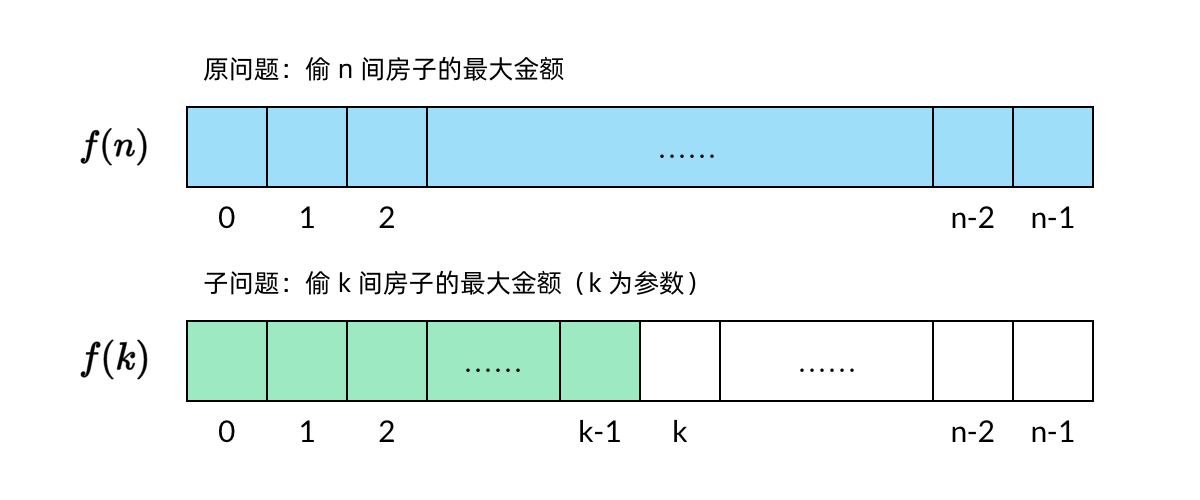
例如这道小偷问题，原问题是“从全部房子中能偷到的最大金额”，
将问题的规模缩小，子问题就是“从k 个房子中能偷到的最大金额”，用 f(k) 表示。

• 可以看到，子问题是参数化的，我们定义的子问题中有参数 k。假设一共有 n 个房子的话，就一共有 n 个子问题。动态规划实际上就是通过求这一堆子问题的解，来求出原问题的解。这要求子问题需要具备两个性质：

• 原问题要能由子问题表示。例如这道小偷问题中，k=nk=n 时实际上就是原问题。否则，解了半天子问题还是解不出原问题，那子问题岂不是白解了。
  一个子问题的解要能通过其他子问题的解求出。例如这道小偷问题中，f(k) 可以由 f(k−1) 和 f(k−2) 求出，具体原理后面会解释。这个性质就是教科书中所说的“最优子结构”。如果定义不出这样的子问题，那么这道题实际上没法用动态规划解。
  小偷问题由于比较简单，定义子问题实际上是很直观的。一些比较难的动态规划题目可能需要一些定义子问题的技巧。

步骤二：写出子问题的递推关系

这一步是求解动态规划问题最关键的一步。然而，这一步也是最无法在代码中体现出来的一步。在做题的时候，最好把这一步的思路用注释的形式写下来。做动态规划题目不要求快，而要确保无误。否则，写代码五分钟，找 bug 半小时，岂不美哉？

我们来分析一下这道小偷问题的递推关系：
假设一共有 nn 个房子，每个房子的金额分别是 H0,H1,...,Hn-1,
子问题f(k) 表示从前 k 个房子（即 H0,H1,...,Hn-1, 中能偷到的最大金额。那么，偷 k 个房子有两种偷法：

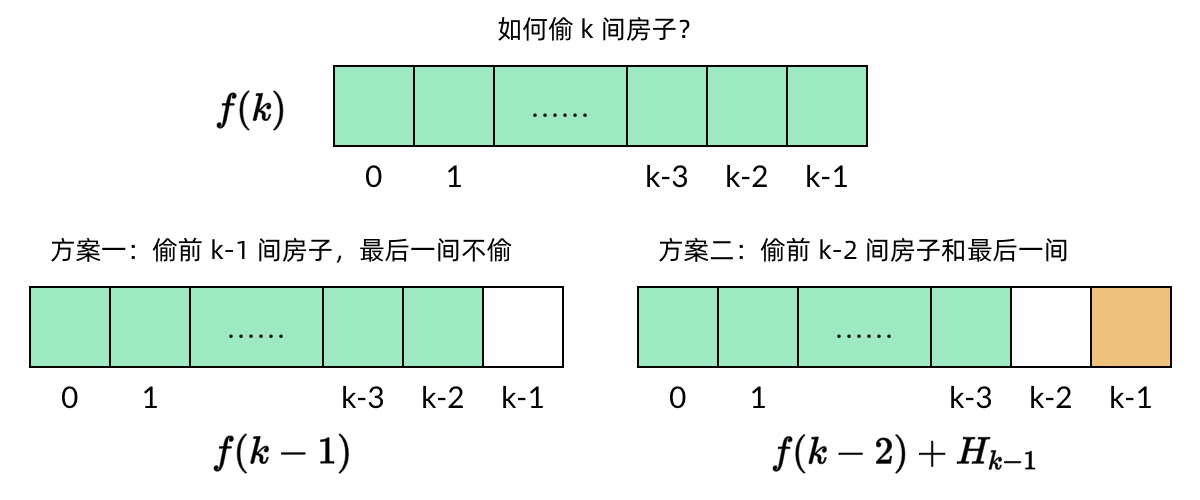
k 个房子中最后一个房子是 Hk-1.如果不偷这个房子，那么问题就变成在前 k-1 个房子中偷到最大的金额，也就是子问题 f(k−1)。如果偷这个房子，那么前一个房子Hk-2显然不能偷
其他房子不受影响。那么问题就变成在前 k−2 个房子中偷到的最大的金额。两种情况中，选择金额较大的一种结果。

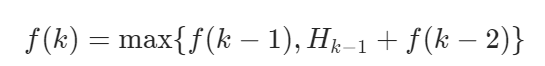
在写递推关系的时候，要注意写k=0和k=1时的情况
k0时没有房子，f(0)=0
k1时，f(1) = H0
这样才能构成完整的递推关系，后面写代码也不容易在边界条件上出错。

步骤三：确定 DP 数组的计算顺序

在确定了子问题的递推关系之后，下一步就是依次计算出这些子问题了。在很多教程中都会写，动态规划有两种计算顺序，一种是自顶向下的、使用备忘录的递归方法，一种是自底向上的、使用 dp 数组的循环方法。不过在普通的动态规划题目中，99% 的情况我们都不需要用到备忘录方法，所以我们最好坚持用自底向上的 dp 数组。

dp[k]对应子问题f(k),即偷前k间房子的最大金额。

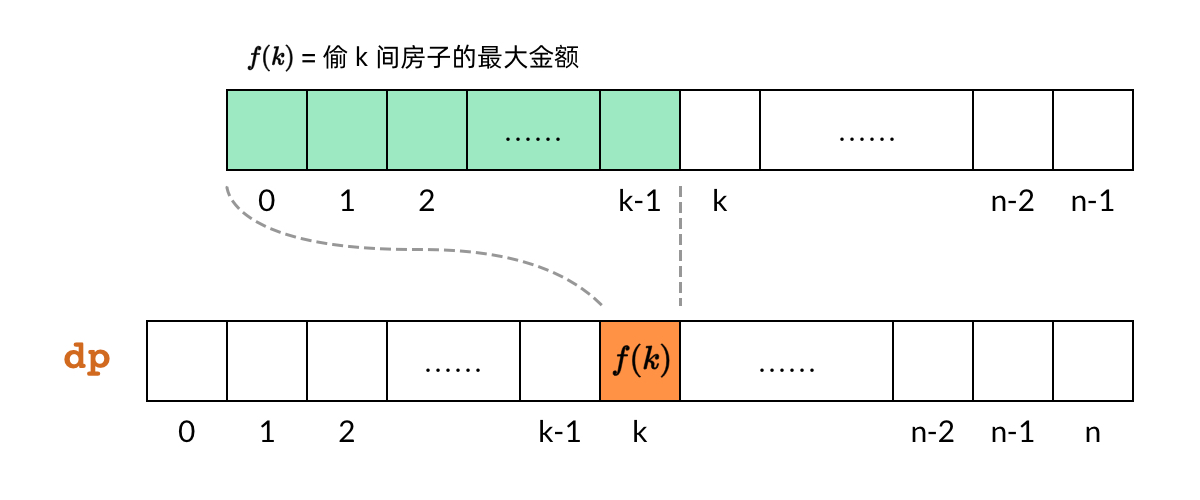
其中，dp[k]依赖dp[k-1]和dp[k-2]

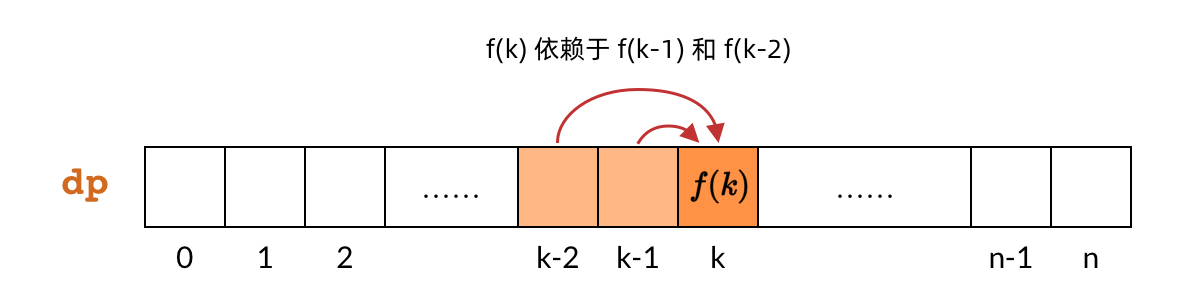
那么，既然 DP 数组中的依赖关系都是向右指的，DP 数组的计算顺序就是从左向右。这样我们可以保证，计算一个子问题的时候，它所依赖的那些子问题已经计算出来了

class Solution {
    public int rob(int[] nums) {
        int len = nums.length;
        if(len<1)
            return 0;
        int[] dp = new int[len+1];
        dp[1] = nums[0];
        for(int i=2;i<=len;i++){
            dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i-1]);
        }
        return dp[len];
    }
}

步骤四：空间优化

空间优化的基本原理是，很多时候我们并不需要始终持有全部的 DP 数组。对于小偷问题，我们发现，最后一步计算 f(n)的时候，实际上只用到了 f(n-1) 和 f(n-2)的结果。n−3 之前的子问题，实际上早就已经用不到了。那么，我们可以只用两个变量保存两个子问题的结果，就可以依次计算出所有的子问题。下面的动图比较了空间优化前和优化后的对比关系：

这样一来，空间复杂度也从 O(n) 降到了O(1)。优化后的代码如下所示：

public int rob(int[] nums) {
    int prev = 0;
    int curr = 0;

    // 每次循环，计算“偷到当前房子为止的最大金额”
    for (int i : nums) {
        // 循环开始时，curr 表示 dp[k-1]，prev 表示 dp[k-2]
        // dp[k] = max{ dp[k-1], dp[k-2] + i }
        int temp = Math.max(curr, prev + i);
        prev = curr;
        curr = temp;
        // 循环结束时，curr 表示 dp[k]，prev 表示 dp[k-1]
    }

    return curr;
}