POI

P5967 Korale

题意

有 \(n\) 个东西，每个东西有价值，随便选出的权值和第 \(k\) 小是多少，并输出方案（权值和相同按照选的集合的字典序排列）。
\(1\le n \le 10^{6},1\le k \le \min (2^{n},10^{6}),1 \le a_{i} \le 10^{9}\)。

题解

第一问：求第 \(k\) 小方案的价值

考虑贪心，将价值从小到大排序，用二元组 \((sum,i)\) 描述前 \(i\) 个数中，选出若干数和为 \(sum\)，其中必选第 \(i\) 个数。利用小根堆不断取出堆顶，并把 \((sum+a[i+1],i+1)\) 和 \((sum+a[i+1]-a[i],i+1)\) 加入堆中，保证不重不漏，时间复杂度 \(O(k\log{n})\)。

第二问：求 \(ans\) 价值下的第 \(cnt\) 个方案

设上一问已经求出：价值为 \(ans\)，字典序第 \(cnt\) 小的方案。
从前向后取数, 每次尽量取靠前的数, 从而保证字典序最小, 取数可以用线段树维护区间最小值因为取得集合排名一定小于等于 \(k\), 所以最多选出 \(k\) 次, 复杂的 \(O(k\log{n})\)。

P5964 Park wodny

题意

一个 \(n\times n\) 的网格图，每个格子是 \(A\) 或 \(B\)，保证 \(B\) 的连通块都是矩形，问把最多两个 \(A\) 变成 \(B\) 后最大的 \(B\) 连通块有多大。\((1\le n \le 10^{3})\)

题解

考虑分类讨论
首先枚举每一个 \(B\) 连通块

情况1：

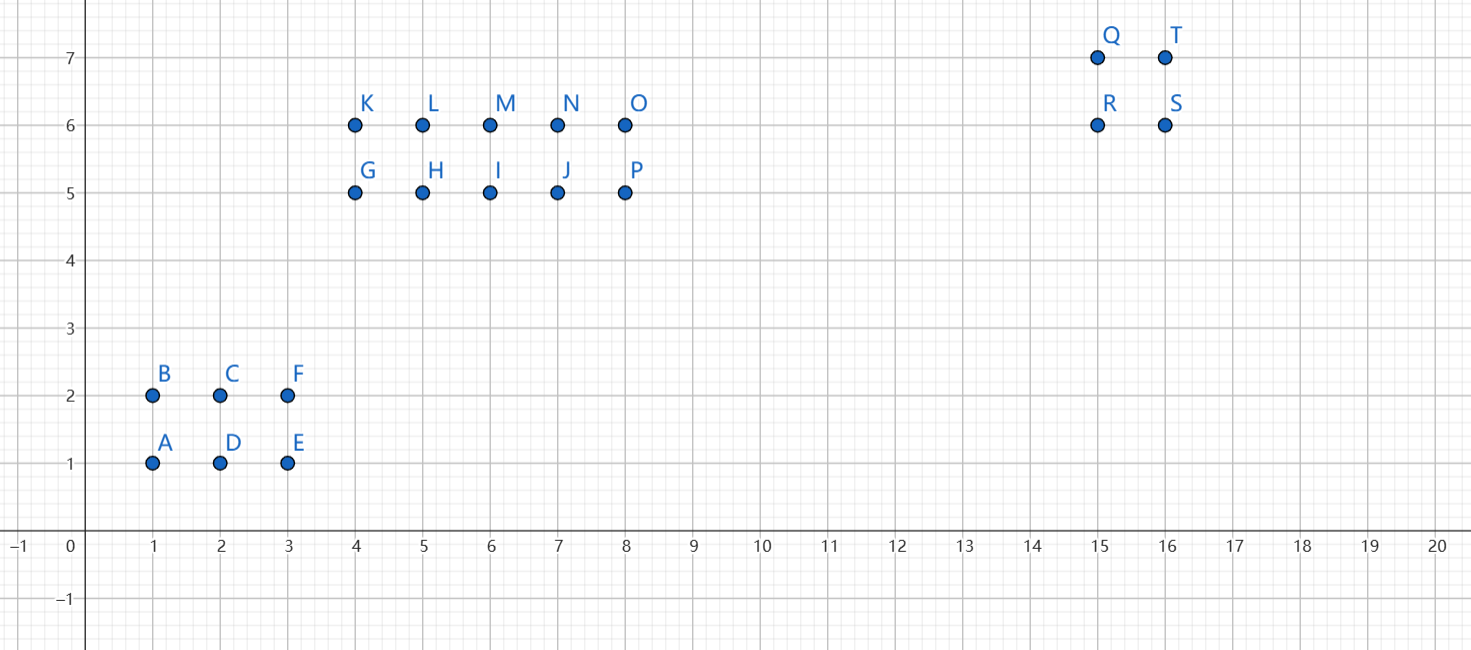
• 任意的一个连通块都无法通过扩展两个点的方式和其他的连通块连通。
• 对于每一个这样的连通块，这个连通块得到的最大贡献是 \(s+2\)，其中 \(s\) 是连通块的大小。

情况2：

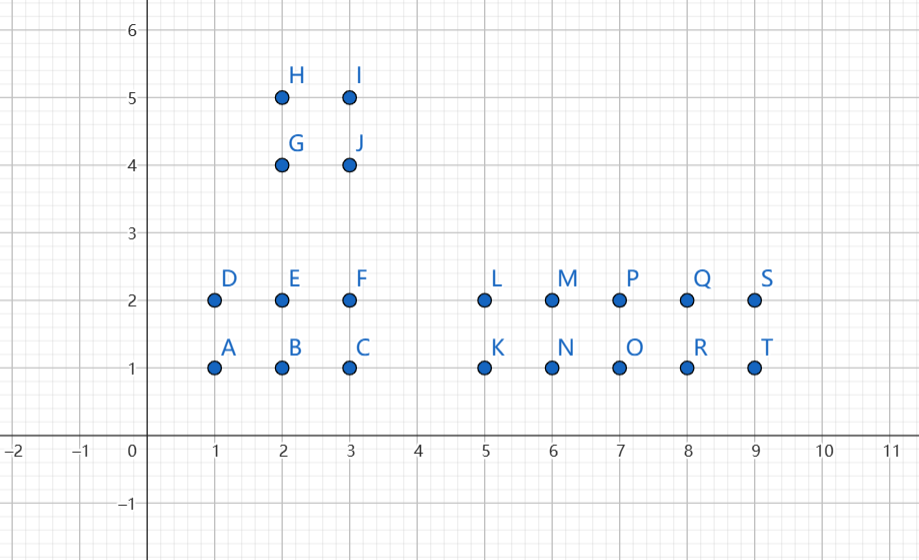
• 对于 \(ABCDEF\) 组成的连通块而言，可以通过对周围扩展和其他的两个连通块连接，贡献为 \(3\) 个连通块的大小的和 \(+2\)。
• 贪心选择两个最大的连通块即可。

情况3：

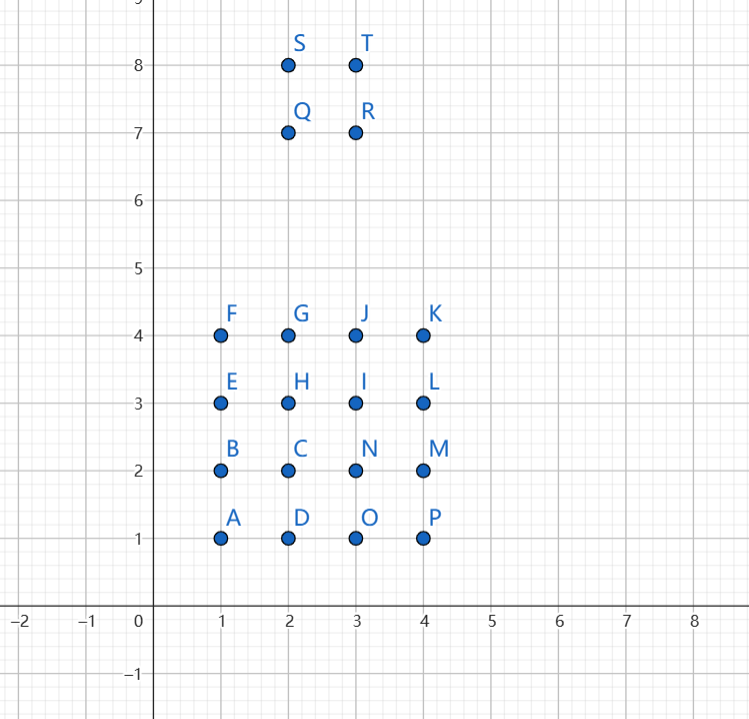
• 上述的两个连通块可以通过扩展两个点来连通，贡献为两个连通块的大小 \(+2\)。

P5969 Nadajniki

题意

一个 \(n\) 个点的树，每个点可以标记多次，一个边如果有端点被标记或者两个端点相邻的点被标记总和大于等于 \(2\) 则这个边合法，问最少标记多少次能使所有边都合法。
\(2\le n \le 2\times 10^{5},1\le a,b\le n\)。

题解（树形 DP）

设 \(dp[i][0/1/2][0/1/2][0/1/2]\) 为第 \(i\) 个点，这个点上放没放，他儿子有没有放，他父亲有没有放，然后转移即可

P5970 Nim z utrudnieniem

题意

有两个人玩游戏，一共 \(m\) 个石子分成 \(n\) 堆，给出每堆石子数量，每轮选择一堆石子并扔掉其中任意个，最后无法扔的人获胜，\(A\) 先手 \(B\) 后手，但是 \(B\) 可以在游戏开始之前扔掉一些堆的石子，不能全扔，且堆数必须是 \(d\) 的倍数，问有多少种扔的方式使 \(B\) 必胜。
\(1\le n \le 5 \times 10^{5},1\le m \le 10^{7},1 \le d \le 10,1 \le a_{i} \le 10^{6}\)。

题解

首先根据 Nim 博弈的结论，各堆石子异或和为 \(0\) 则后手必胜，否则先手必胜，那么就是统计多少种取法使异或和为 \(0\)。
异或的一个性质：对于任何整数 \(A\)，必然有 \(A\bigoplus A=0\)，因此我们可以记录原来 \(n\) 堆石子的异或和 \(s\)，将题目转化为为了取 \(k\times d\) 堆石子，问有多少种方法让取到的石子堆中每堆石子的异或和为 \(s\)。

\(dp\) 转移方程：\(dp[i][j][k]=dp[i-1][j][k]+dp[i-1][j-1][k\bigoplus a[i]]\)

表示前 \(i\) 堆石子，取出模 \(d\) 余 \(j\) 堆石子，取出的石子异或和为 \(k\)。
发现空间会炸，于是考虑像背包一样倒序转移，滚掉第一维。发现这样 \(dp\) 的时间复杂度为 \(O(nd\times \max (a_{i}))\)，还是不行。

优化（本题核心）：

因为对于任意一个正整数 \(A\)，它和比它自己小的数字异或起来的结果不会超过 \(A\times 2\)。也就是一个数异或上一些比它小的数后，二进制下的位数不变。设 \(x\) 表示二进制下与 \(A\) 位数相同的最大的数，则 \(x\le 2A\)。那么我们把 \(a_{i}\) 从小到大排序，每次只枚举 \(a_{i}\) 到对应的 \(x\)，复杂度就降到了 \(O(md)\)。

P5956 Podzielno

题意

\(B\) 进制数，每个数字 \(i∈[0,B)\) 有 \(a_{i}\) 个。你要用这些数字组成一个最大的 \(B\) 进制数 \(X\) （不能有前导零，不需要用完所有数字），使得 \(X\) 是 \(B−1\) 的倍数。\(q\) 次询问，每次询问 \(X\) 在 \(B\) 进制下的第 \(k\) 位数字是什么(最低位是第 \(0\) 位)。
\(2\le B \le 10^{6},1\le q\le 10^{5},1\le a_{i} \le 10^{6},0\le k\le 10^{18}\)。

题解

首先我们需要知道若 \(X\) 是 \(B-1\) 的倍数，则各位数字加和一定也是 \(B-1\) 的倍数。

证明

设 \(X\) 是 \(B−1\) 的倍数，将 \(X\) 拆分成 \(B\) 进制后，就为\(a_{0}\times B^{0}+a_{1}\times B^{1}+a_{2}\times B^{2}+……+a_{k}\times B^{k}\)。也就是说\((a_{0}\times B^{0}+a_{1}\times B^{1}+a_{2}\times B^{2}+……+a_{k}\times B^{k}) \bmod (B-1)=0\)。将每一项分别 \(\bmod\)，我们会发现对于每一个 \(B^{k} \bmod (B-1)=1\)。可以理解为将其拆分成\(B\times B\times B\times B\times ……\times B\) 的形式，每一个都 \(\bmod (B-1)\)，刚好为 \(1\)。所以，\((a_{0}+a_{1}+a_{2}+……+a_{k})\bmod (B-1)=0\)。

当选择所有数不满足条件时，由于 \(a_{i}\ge 1\)，只需要删除对应的一个数字即可。之后将所有数字 \(i\) 从大到小排列就是最大的 \(X\)。

P5957 Flappy Bird

题意

一开始小鸟在 \((0,0)\)，他需要飞到横坐标为 \(X\) 的任意位置上，每一秒可以点击屏幕使得它从 \((x,y)\) 移动到 \((x+1,y+1)\)，也可以不点移动到 \((x+1,y-1)\)，有 \(n\) 个障碍物，在 \(x_{i}\) 位置并且挡住了 \(y\) 小于等于 \(a_{i}\) 的区域和大于等于 \(b_{i}\) 的位置，问最少点几次屏幕能到达目标或输出不可到达。
\(0\le n\le 5\times 10^{5},1\le X \le 10^{9},0<x_{i}<X,-10^{9}\le a_{i}\le b_{i}\le 10^{9}\)。

题解

发现点击的次数只和到终点时的 \(y\) 坐标有关。
考虑 \(dp_{i,0/1}\) 表示到达第 \(i\) 个障碍物时候最小/最大的 \(y\) 坐标是什么，转移考虑从上一次的最低最高点飞过来，再考虑距离的奇偶性即可。

dp 转移方程：

\(dp_{i,0}=\max(a_{i}+1+(x_{i}\bmod2=1)\bigoplus(\left\vert a_{i}+1\right\vert \bmod2=1)),dp_{i-1,0}-(x_{i}-x_{i-1}))\)

\(dp_{i,1}=\min(b_{i}-1-(x_{i}\bmod2=1)\bigoplus(\left\vert b_{i}-1\right\vert \bmod2=1)),dp_{i-1,1}+(x_{i}-x_{i-1}))\)

注意如果某个点 \(dp_{i,0}>dp_{i,1}\)，那么说明不可能到达。

P5958 Sabotaż

题意

\(n\) 个点的数，开始任意一个点是黑点，如果一个点子树中（不包括自己）黑点比例超过 \(x\) 则这个点子树（包括自己）里所有点都变成黑点，问最小的 \(x\) 使得最坏情况下黑点数量不超过 \(k\)。
\(1\le k \le n\le 5\times 10^{5},1\le p_{i+1}\le i\)。

题解（树形 DP）

本题有如下性质：

1. 最坏情况下，最开始的叛徒是叶子结点
2. 因为一个节点被染黑了，以其为根节点的子树将全黑，所以最终被染黑的一定是一颗子树
   考虑数组 \(dp[i]\) 表示使这个节点变黑的最大值，同时也是使这个节点不变黑的最小值。也就是说如果我们的 \(x\) 大于了这个值，那么这个节点就不变黑，反之，就变黑。
   可知 \(dp[i]\) 仅与 \(dp[j]\) 以及 \(j\) 的大小有关（这里的 \(j\) 表示 \(i\) 的子节点）
   \(sz[i]\) 表示以 \(i\) 为根节点的子树的大小。
   显然 \(i\) 被染黑必须满足以下两种情况：
3. \(dp[j]>x\),即i的某棵子树被染黑
4. \(sz[j]/(sz[i]-1)>x\),即 \(j\) 子树（包括 \(j\)）在 \(i\) 子树（不包括 \(i\)）中比例超过 \(x\)，\(j\) 子树被染黑足以导致以 \(i\) 为根的整棵子树被染黑
   根据以上规律可以推出如下方程：

\(dp[i]=\max (dp[i],\min (dp[j],sz[j]/(sz[i]-1))\)

取 min 是因为需要同时满足条件 \(1\) 和条件 \(2\)。
取 max 是因为需要答案最优，要取到使 \(i\) 变黑的最大 \(x\)，也就是使得 \(i\) 不变黑的最小 \(x\)。

注意

1. 对于叶子结点 \(u\)，显然有 \(dp[u]=1\)。
2. 对于 \(ans\) 当 \(sz[u]<k\) 时是不需要考虑的，因为它合法，所以即使它被染黑也无所谓。
3. 针对上一条结论，得到 \(ans=\max (ans,dp[u])\),其中\(sz[u]\le k\)。

P5968 Reprezentacje ró?nicowe

题意

一个数列 \(a\)。
当 \(n\le 2\) 时，\(a_{n}=n\)。
当 \(n>2\) 时，且 \(n\) 为奇数时，\(a_{n}=2\times a_{n-1}\)。
当 \(n>2\) 时，且 \(n\) 为偶数时，\(a_{n}=a_{n-1}+r_{n-1}\)。
\(r_{n}= mex (\left\vert a_{i}-a_{j} \right\vert) (1\le i\le j\le n-1)\),mex \((S)\) 表示最小的不在 \(S\) 里的非负整数。
\(n\) 次询问每次给一个正整数 \(x\) 要求把 \(x\) 表示为 \(a_{i}-a_{j}\) 并输出 \(i\) 和 \(j\)。
\(1\le n\le 10^{5},1\le x\le 10^{9}\)。

题解

因为任意两个 \(a\) 的差不会相同，且 \(a_{56}=1062283805\)，超出 \(10^{9}\)。对于大小超过 \(10^{9}\) 的数，奇数位和前一项偶数位的差也大于 \(10^{9}\)， 所以此时答案，不超过 \(10^{9}\) 的差只能是偶数位与前一项奇数位的差。
所以我们可以暴力打出 \(10^{9}\) 以内的数（实际上只有 \(56\) 项）。查询时，如果在前面 \(56\) 项里查到了就输出。否则因为此时的答案递增，所以每一个在前 \(56\) 项查不到的 \(x\)，都从小到大依次对应一个 \(10^{9}\) 以外的一对数。设 num 为前面暴力打出的小于 \(x\) 的差的数量，则答案为\((56+(x-num)\times 2,56+(x-num)\times 2-1)\)。

P5955 Pionek

题意

给出 \(n\) 个平面向量，要求选择一些向量使它们和的模长最大，输出最大模长。
\(n\le 2\times 10^{5},\left\vert x \right\vert,\left\vert y \right\vert \le 10^{4}\)。

题解

假设已知答案向量方向，观察题目可以发现，只有在答案向量方向投影为正的向量才会对结果产生贡献。由此考虑枚举所有方向。
对所有向量的极角排序，排序后可以确定选取的向量一定是连续的一段。考虑使用双指针求解。所有的向量形成一个环，因此处理时需要复制一份求解，然后双指针枚举左右端点即可得出结果。