Android中图像变换Matrix的原理

转载自：http://blog.csdn.net/pathuang68/article/details/6991867

在Android中，如果你用Matrix进行过图像处理，那么一定知道Matrix这个类。Android中的Matrix是一个3 x 3的矩阵，其内容如下：

 

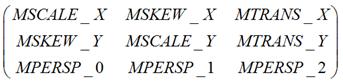
Matrix的对图像的处理可分为四类基本变换：

Translate           平移变换

Rotate                旋转变换

Scale                  缩放变换

Skew                  错切变换

 

从字面上理解，矩阵中的MSCALE用于处理缩放变换，MSKEW用于处理错切变换，MTRANS用于处理平移变换，MPERSP用于处理透视变换。实际中当然不能完全按照字面上的说法去理解Matrix。同时，在Android的文档中，未见到用Matrix进行透视变换的相关说明，所以本文也不讨论这方面的问题。

 

针对每种变换，Android提供了pre、set和post三种操作方式。其中

set用于设置Matrix中的值。

pre是先乘，因为矩阵的乘法不满足交换律，因此先乘、后乘必须要严格区分。先乘相当于矩阵运算中的右乘。

post是后乘，因为矩阵的乘法不满足交换律，因此先乘、后乘必须要严格区分。后乘相当于矩阵运算中的左乘。

 

除平移变换(Translate)外，旋转变换(Rotate)、缩放变换(Scale)和错切变换(Skew)都可以围绕一个中心点来进行，如果不指定，在默认情况下是围绕(0, 0)来进行相应的变换的。

 

下面我们来看看四种变换的具体情形。由于所有的图形都是有点组成，因此我们只需要考察一个点相关变换即可。

 

一、 平移变换

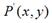假定有一个点的坐标是 ，将其移动到 ，再假定在x轴和y轴方向移动的大小分别为：

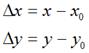
如下图所示：

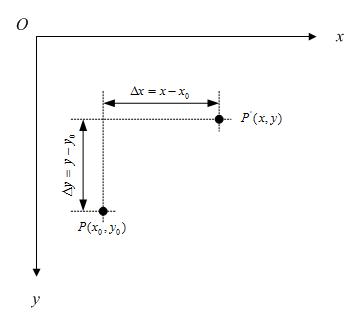
不难知道：

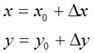
如果用矩阵来表示的话，就可以写成：

 

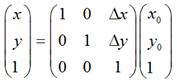
二、 旋转变换

 

2.1    围绕坐标原点旋转：

假定有一个点 ，相对坐标原点顺时针旋转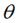后的情形，同时假定P点离坐标原点的距离为r，如下图：

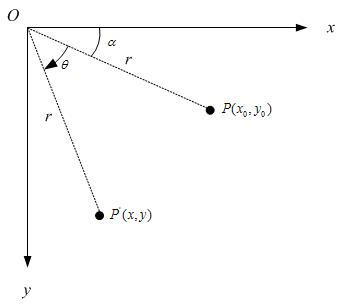
那么，

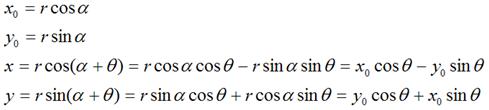
如果用矩阵，就可以表示为：

 

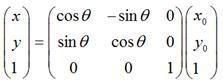
2.2    围绕某个点旋转

如果是围绕某个点顺时针旋转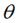，那么可以用矩阵表示为：

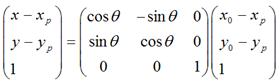
可以化为：

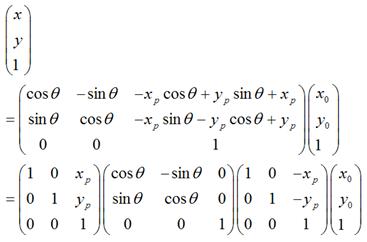
很显然，

1.   

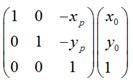  是将坐标原点移动到点后， 的新坐标。

2.     

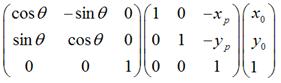
是将上一步变换后的，围绕新的坐标原点顺时针旋转 。

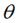3.     

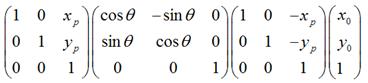
经过上一步旋转变换后，再将坐标原点移回到原来的坐标原点。

 

所以，围绕某一点进行旋转变换，可以分成3个步骤，即首先将坐标原点移至该点，然后围绕新的坐标原点进行旋转变换，再然后将坐标原点移回到原先的坐标原点。

 

三、 缩放变换

理论上而言，一个点是不存在什么缩放变换的，但考虑到所有图像都是由点组成，因此，如果图像在x轴和y轴方向分别放大k1和k2倍的话，那么图像中的所有点的x坐标和y坐标均会分别放大k1和k2倍，即

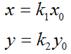
用矩阵表示就是：

缩放变换比较好理解，就不多说了。

 

四、 错切变换

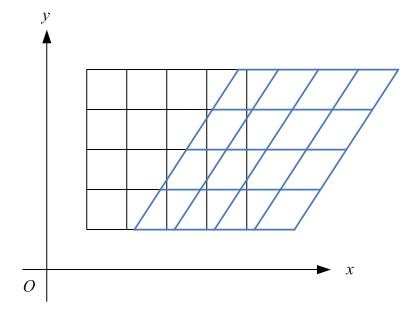
错切变换(skew)在数学上又称为Shear mapping(可译为“剪切变换”)或者Transvection(缩并)，它是一种比较特殊的线性变换。错切变换的效果就是让所有点的x坐标(或者y坐标)保持不变，而对应的y坐标(或者x坐标)则按比例发生平移，且平移的大小和该点到x轴(或y轴)的垂直距离成正比。错切变换，属于等面积变换，即一个形状在错切变换的前后，其面积是相等的。

比如下图，各点的y坐标保持不变，但其x坐标则按比例发生了平移。这种情况将水平错切。

下图各点的x坐标保持不变，但其y坐标则按比例发生了平移。这种情况叫垂直错切。

 

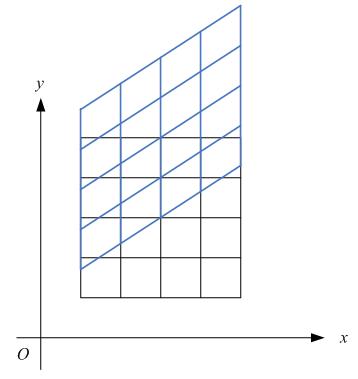
假定一个点经过错切变换后得到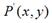，对于水平错切而言，应该有如下关系：

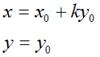
用矩阵表示就是：

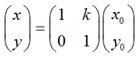
扩展到3 x 3的矩阵就是下面这样的形式：

 

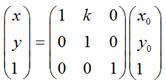
同理，对于垂直错切，可以有：

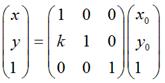
在数学上严格的错切变换就是上面这样的。在Android中除了有上面说到的情况外，还可以同时进行水平、垂直错切，那么形式上就是：

 

五、 对称变换

除了上面讲到的4中基本变换外，事实上，我们还可以利用Matrix，进行对称变换。所谓对称变换，就是经过变化后的图像和原图像是关于某个对称轴是对称的。比如，某点 经过对称变换后得到，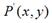

如果对称轴是x轴，难么，

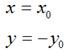
用矩阵表示就是：

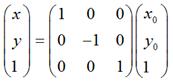
如果对称轴是y轴，那么，

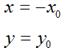
用矩阵表示就是：

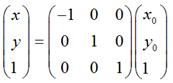
如果对称轴是y = x，如图：

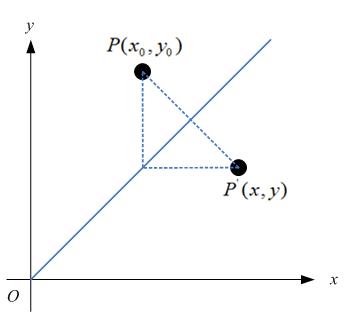
那么，

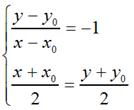
很容易可以解得：

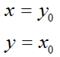
用矩阵表示就是：

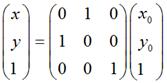
同样的道理，如果对称轴是y = -x，那么用矩阵表示就是：

 

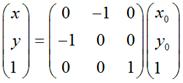
特殊地，如果对称轴是y = kx，如下图：

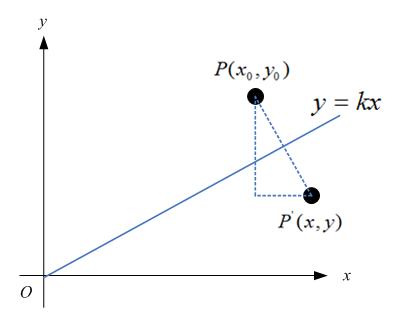
那么，

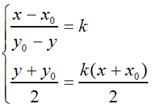
很容易可解得：

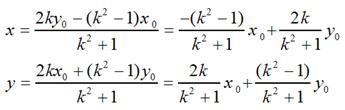
用矩阵表示就是：

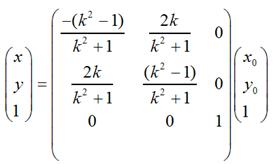
当k = 0时，即y = 0，也就是对称轴为x轴的情况；当k趋于无穷大时，即x = 0，也就是对称轴为y轴的情况；当k =1时，即y = x，也就是对称轴为y = x的情况；当k = -1时，即y = -x，也就是对称轴为y = -x的情况。不难验证，这和我们前面说到的4中具体情况是相吻合的。

 

如果对称轴是y = kx + b这样的情况，只需要在上面的基础上增加两次平移变换即可，即先将坐标原点移动到(0, b)，然后做上面的关于y = kx的对称变换，再然后将坐标原点移回到原来的坐标原点即可。用矩阵表示大致是这样的：

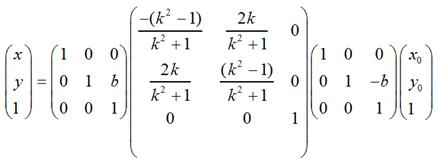
需要特别注意：在实际编程中，我们知道屏幕的y坐标的正向和数学中y坐标的正向刚好是相反的，所以在数学上y = x和屏幕上的y = -x才是真正的同一个东西，反之亦然。也就是说，如果要使图片在屏幕上看起来像按照数学意义上y = x对称，那么需使用这种转换：

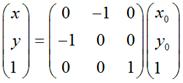
要使图片在屏幕上看起来像按照数学意义上y = -x对称，那么需使用这种转换：
 

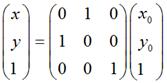
关于对称轴为y = kx 或y = kx + b的情况，同样需要考虑这方面的问题。

下面是Matrix矩阵的实现的部分代码，对照上面的理论进行解释：@author:qhyuan

public class Matrix extends _Original_Matrix {

    float mValues[] = new float[9];
...
    /**
     * Adds the given transformation to the current Matrix
     * <p/>This in effect does this = this*matrix
     * @param matrix
     */
    private void addTransform(float[] matrix) {
        float[] tmp = new float[9];

        // first row
        tmp[0] = matrix[0] * mValues[0] + matrix[1] * mValues[3] + matrix[2] * mValues[6];
        tmp[1] = matrix[0] * mValues[1] + matrix[1] * mValues[4] + matrix[2] * mValues[7];
        tmp[2] = matrix[0] * mValues[2] + matrix[1] * mValues[5] + matrix[2] * mValues[8];

        // 2nd row
        tmp[3] = matrix[3] * mValues[0] + matrix[4] * mValues[3] + matrix[5] * mValues[6];
        tmp[4] = matrix[3] * mValues[1] + matrix[4] * mValues[4] + matrix[5] * mValues[7];
        tmp[5] = matrix[3] * mValues[2] + matrix[4] * mValues[5] + matrix[5] * mValues[8];

        // 3rd row
        tmp[6] = matrix[6] * mValues[0] + matrix[7] * mValues[3] + matrix[8] * mValues[6];
        tmp[7] = matrix[6] * mValues[1] + matrix[7] * mValues[4] + matrix[8] * mValues[7];
        tmp[8] = matrix[6] * mValues[2] + matrix[7] * mValues[5] + matrix[8] * mValues[8];

        // copy the result over to mValues
        mValues = tmp;
    }
    
    /** Set the matrix to translate by (dx, dy). */
    //平移的增量dx和dy对应于矩阵中的a(0,2)和a(1,2)  @auth:qhyuan
    @Override
    public void setTranslate(float dx, float dy) {
        mValues[0] = 1;
        mValues[1] = 0;
        mValues[2] = dx;
        mValues[3] = 0;
        mValues[4] = 1;
        mValues[5] = dy;
        mValues[6] = 0;
        mValues[7] = 0;
        mValues[8] = 1;
    }
    /**
     * Set the matrix to rotate by the specified number of degrees, with a pivot
     * point at (px, py). The pivot point is the coordinate that should remain
     * unchanged by the specified transformation.
     */
     //该函数是围绕着指定的(px,py)进行旋转，转换矩阵由三部分构成
    @Override
    public void setRotate(float degrees, float px, float py) {
        // TODO: do it in one pass
				//第一步：对应于第三个矩阵
        // translate so that the pivot is in 0,0
        mValues[0] = 1;
        mValues[1] = 0;
        mValues[2] = -px;
        mValues[3] = 0;
        mValues[4] = 1;
        mValues[5] = -py;
        mValues[6] = 0;
        mValues[7] = 0;
        mValues[8] = 1;

        // scale
        double rad = Math.toRadians(degrees);
        float cos = (float)Math.cos(rad);
        float sin = (float)Math.sin(rad);
        //第二步：在上面得到的矩阵前面左乘以矩阵
        addTransform(new float[] { cos, -sin, 0, sin, cos, 0, 0, 0, 1 });
        // translate back the pivot
        //第三步再在前面左乘一个矩阵
        addTransform(new float[] { 1, 0, px, 0, 1, py, 0, 0, 1 });
    }
...
}