2021.11.11 模拟赛总结

Ⅰ. 串串串

问题描述：

你有两个长度分别为 n,m 的 01 串 S,T 。

有 Q 次询问，每次询问给出 l1,r1,l2,r2 ，满足 r1−l1+1=r2−l2+1 。令 a=S[l1…r1] ， b=T[l2…r2] ，你需要求出 ai≠bi 的位置个数对 2 取模的结果。

输入格式：

第一行两个正整数 n,m ，分别表示 S,T 的长度。

接下来两行输入两个 01 串表示 S 和 T 。

接下来一行一个整数 Q ，表示询问的个数。

接下来 Q 行，每行四个整数 l1,r1,l2,r2, 表示一组询问。

输出格式：

对于每组询问，输出一个数 0 或 1 表示答案。

数据范围：

对于 30% 的数据： n,m,q≤5000 ；
对于 70% 的数据： n,m,q≤5×104 ；
对于 80% 的数据： n,m,q≤105 ；
对于 100% 的数据： 1≤n,m,q≤2×105 ， 1≤l1≤r1≤n ， 1≤l2≤r2≤m 。

 

 

　　注意到这道题的答案对 2 取模，即，只需回答奇偶性。

 

　　字符串 a 、b 存在以下三种情况：

　　　　1. '0' 和 '1' ：贡献为 1 ；

　　　　2. '0' 和 '0' ：贡献为 0；

　　　　3. '1' 和 '1' ：贡献为 0，但与 2 奇偶性相同。

 

　　所以：我们只需要统计区间中 1 的个数的奇偶性就可以。

 

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
int n,m,q,A[200005],B[200005];
#define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1,*p2;
inline int read()
{
    char ch;int x(0);while((ch=gc)<48);
    do x=x*10+ch-48;while((ch=gc)>=48);
    return x;
}
inline int Read()
{
    char ch;int x(0);while((ch=gc)<48);
    x=ch-48;return x;
}
int main()
{
    n=read(),m=read();
    for(register int i=1;i<=n;++i) A[i]=A[i-1]+Read();
    for(register int i=1;i<=m;++i) B[i]=B[i-1]+Read();
    q=read();
    for(register int i=1,l,r,ll,rr;i<=q;++i)
    l=read(),r=read(),ll=read(),rr=read(),printf("%d\n",(A[r]-A[l-1]+B[rr]-B[ll-1])&1);
    return 0;
}

 

---

 

Ⅱ. 方格计数

问题描述：

在左下角是 (0,0) ，右上角是 (W,H) 的网格上，有 (W+1)×(H+1) 个格点。

现在要在格点上找 N 个不同的点，使得这些点在一条直线上。并且在这条直线上，相邻点之间的距离不小于 D 。

求方案数模 109+7 。

输入格式：

第一行一个整数 T ，表示数据组数。

接下来 T 行，每行四个整数 N,W,H,D ，意义如题目描述。

输出格式：

T 行, 每行一个整数表示答案。

数据范围：

对于 20% 的数据： N,W,H,D≤10 。
对于 50% 的数据： W,H,D≤100 。
对于另 20% 的数据： N≤5 。
对于 100% 的数据： 1≤N≤50 ， 1≤W,H,D≤500 ， 1≤T≤20 。

 

 

前置：

　　1. 在一个以 (0,0) 开始的二维网格中，一条线段 (0,0)−(x,y) 含有整数点的个数为 gcd(x,y)−1（不包含线段的两个整数端点）

　　2. 有 n个盒子，从中选 m 个，且相邻两个盒子之间至少有 k 个盒子的组合方案为 ：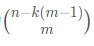

 

 

　　首先，暴力很好想，枚举两个端点，横坐标之差的绝对值为 x ，纵坐标之差的绝对值为 y ，那么这里面包含的整数点个数为 gcd( x , y ) - 1 ，强制两个端点必须选，那么剩下还要选 n−2 个，

　　求出相邻两个盒子之间编号差至少为 k，即两个盒子之间的盒子个数至少为k−1，两个端点选了会导致两个 k−1 的长度区间盒子不能选 ，剩下的盒子数只有 g−1−2(k−1)

　　套用上面的组合数公式。不难发现，最后只与横纵坐标差有关，所以直接枚举横纵坐标差，乘以情况数 (w−x+1)(h−y+1) 。

　　但是这个差是绝对值差，所以如果不是水平或竖直线，就有两种情况。

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define int long long
#define mod 1000000007
using namespace std;
int _,n,w,h,d,C[505][505],Ans;
#define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++)
char buf[65536],*p1,*p2;
inline int read()
{
    char ch;int x(0);while((ch=gc)<48);
    do x=x*10+ch-48;while((ch=gc)>=48);
    return x;
}
inline void Pre()
{
    for(register int i=0;i<=500;++i)
        {
            C[i][0]=C[i][i]=1;
            for(register int j=1;j<i;++j) C[i][j]=(1LL*C[i-1][j]+C[i-1][j-1])%mod;
        }
}
inline int Gcd(int x,int y) {return y?Gcd(y,x%y):x;}
inline double Work(int x,int y) {return sqrt(x*x*1.0+y*y);}
inline int Get(int x,int y)
{
    if(!x&&!y) return 0;int g=Gcd(x,y);
    int k=(int)ceil(d/Work(x/g,y/g));if(k*(n-1)>g) return 0;
    int RET=C[g-1-2*(k-1)-(k-1)*(n-3)][n-2];
    if(x&&y) RET=((1LL*RET)<<1)%mod;
    return 1LL*RET*(w-x+1)%mod*(h-y+1)%mod;
}
signed main()
{
    _=read(),Pre();
    for(register int __=1;__<=_;++__)
    {
        n=read(),w=read(),h=read(),d=read(),Ans=0;
        if(n==1) {printf("%lld\n",(w+1)*(h+1));continue;}
        for(register int i=0;i<=w;++i)
            for(register int j=0;j<=h;++j) Ans=(1LL*Ans+Get(i,j))%mod;
        printf("%lld\n",Ans);
    }
    return 0;
}

 

---

 

Ⅲ. 树数树

问题描述：

 输入格式：

第一行一个正整数 T ，表示数据组数。

对于每组数据第一行一个正整数 n 。

接下来 n−1 行, 每行两个正整数 u,v ，表示树上的一条边。

输出格式：

T 行, 每行一个整数表示每组数据的答案。

数据范围：

对于 100% 的数据： 1≤T≤5 ， 2≤n≤10e5 ， 1≤u,v≤n ， u≠v ，输入保证是一棵树。

 

　　首先，不难发现：对于一条链或一颗二叉树，所有节点是可以选完的；而菊花图最多只能选出 3 个点；

　　不难推出：x 的最大贡献为其子树中最大两个贡献之和加 1 ；

　　

　　考虑怎么维护？

　　 很容易想道优先队列（堆）（当然，线段树也可），对每个点进行维护，注意要用 “ 启发式合并 ” 。

 

Code：

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define int long long
#define mod 1000000007
using namespace std;
int _,n,w,h,d,C[505][505],Ans;
#define gc (p1==p2&&(p2=(p1=buf)+fread(buf,1,65536,stdin),p1==p2)?EOF:*p1++)
char buf[65536],*p1,*p2;
inline int read()
{
    char ch;int x(0);while((ch=gc)<48);
    do x=x*10+ch-48;while((ch=gc)>=48);
    return x;
}
inline void Pre()
{
    for(register int i=0;i<=500;++i)
        {
            C[i][0]=C[i][i]=1;
            for(register int j=1;j<i;++j) C[i][j]=(1LL*C[i-1][j]+C[i-1][j-1])%mod;
        }
}
inline int Gcd(int x,int y) {return y?Gcd(y,x%y):x;}
inline double Work(int x,int y) {return sqrt(x*x*1.0+y*y);}
inline int Get(int x,int y)
{
    if(!x&&!y) return 0;int g=Gcd(x,y);
    int k=(int)ceil(d/Work(x/g,y/g));if(k*(n-1)>g) return 0;
    int RET=C[g-1-2*(k-1)-(k-1)*(n-3)][n-2];
    if(x&&y) RET=((1LL*RET)<<1)%mod;
    return 1LL*RET*(w-x+1)%mod*(h-y+1)%mod;
}
signed main()
{
    _=read(),Pre();
    for(register int __=1;__<=_;++__)
    {
        n=read(),w=read(),h=read(),d=read(),Ans=0;
        if(n==1) {printf("%lld\n",(w+1)*(h+1));continue;}
        for(register int i=0;i<=w;++i)
            for(register int j=0;j<=h;++j) Ans=(1LL*Ans+Get(i,j))%mod;
        printf("%lld\n",Ans);
    }
    return 0;
}