数学专练

　　（本篇博客不含题面(但有连接)、详解，主要是关键点和总结）

 

Ⅰ. Paperfolding

　　很容易推出答案为：

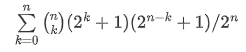
 　　然后用二项式定理化简，二项式定理如下：

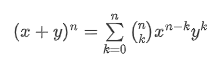
 　　化简之后可得：

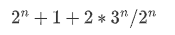
 　　最后快速幂+逆元。

   

 

Ⅱ. Divisors

　　观察范围：我们只需要输出前100000项，所以直接大法师。

　　注意预先 √n 处理因数，并 “适当” 加入 return （即剪枝）。

 

 

Ⅲ. So Easy!

　　推导：

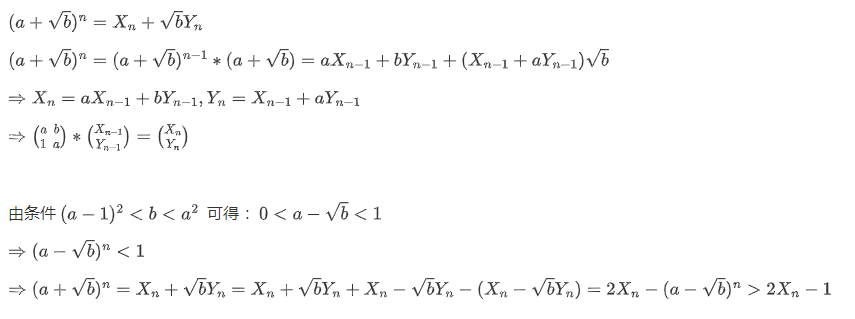
 　　最后矩阵快速幂一下。

 

 

Ⅳ. Mathematician QSC

　　首先，显然：

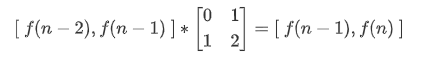
 　　考虑怎么化简 g()：

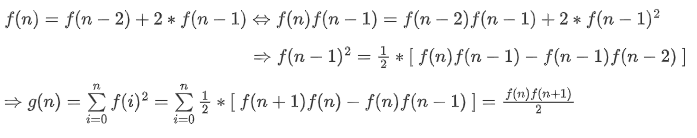
 　　到这就完了吗？

　　想多了，那个 /2 怎么办？在 %S 意义下，2 很有可能没有逆元。

　　小知识：（读者自证不难）

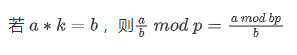
 　　最后记得求欧拉函数（S可能为非质数）。

 

 

Ⅴ. 上升数

　　遇见这种类型的题，我们一般有两种套路：找倍数删除不合法的，找合法的删除非倍数的

　　显然对于这道题，我们去数位DP找合法是行不通的，n 有 1e18 的规模。所以，我们需要去找倍数。

 

　　不难发现，讨论从右往左的第 x 位，如果它比它的上一位大 Del ，那么整个数增加了 11...1(x 个) * Del 。

　　那么题面可以等同于：求至多九个完全由1组成的数，它们的和是 k 的倍数的方案数。

 

　　由于我们是在找倍数，所以，同余是可以放在一起讨论的，统计出每个余数出现的次数（即：% p == x ）。

　　怎么统计？

　　暴力枚举 1 , 11 , 111 , 1111 ... 显然这是有周期性的。

 

　　现在可以愉快的DP了：

　　设 f [ i ] [ j ] [ k ] 表示处理过余数为0∼i−1的 ，选择了j个数，当前余数为k的方案数。(状态鬼畜)，

　　枚举 x ，表示选择 x 个余数为 i 的 ，转移至 f [ i + 1 ] [ j + x ] [ ( k + x * i ) % p ] ，

　　考虑转移系数，由于可以在一个位置多选，所以，该问题为 多重集的组合数 ：

 　　　　

 　　最后，初始化：第 n 为必选，所以，f [ 0 ] [ 1 ] [ t ] = 1 ( t 表示 n 个 1 mod p )。

 

 

Ⅵ. Relatively Prime Powers

　　这种题可以往两个方向思考：找合法，去非法。

　　显然，这道题找合法的似乎有亿点点困难，所以我们去非法的。

 

　　非法的一定是某个数的次方(或经转换)，比如， 2² * 3⁴ = 18²

　　找出 n 范围内的 每个次方 的数量，进行容斥。